Эконометрический анализ цен на молоко.
Задание №1. Первичная обработка исходных данных
1. Собрать n=360-365 данных любого года по акциям ведущих компаний России. В следующем виде:
Например:
| № дня или t | дата | Цена открытия |
| 1 мая 2013 | 32, 745 | |
| 2 мая | 32, 795 | |
| .......... | ............ | ............................................ |
| 1 мая 2014 | 31, 195 |
2. По цене открытия построить гистограмму.
3. Провести первичную статистическую обработку данных. Использовать опции Данные →Анализ данных→Описательная статистика
4. Исследовать данные на однородность. Использовать коэффициент вариации
Vy = (σy/ 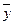 ) 100%.
) 100%.
При этом следует ответить на вопрос: нужно ли разные порции данных обрабатывать разными способами?
1. Результаты обработки описать.
Сгруппировать описание по категориям:
А) Мода, медиана, среднее значение, асимметрия
Б) Эксцесс, дисперсия, среднеквадратичное отклонение .
2. Отсортировать данные и сгруппировать их в k = 3,22* ln(n) + 1 групп.
С помощью функции ЧАСТОТА определить количество данных попавших в каждую группу. Построить график частот. На этом графике показать моду, медиану, среднее значение, асимметрию, эксцесс.
3. По гистограмме построить 5 типов линий тренда. Выбрать из них наилучшую по R2. И по экономическим соображениям.
Написать краткую характеристику компании. Текст пишется в редакторе WORD шрифтом 12 не менее 0,5 страницы. Например:
ОЙЛ - ведущая вертикально-интегрированная нефтяная компания России, история которой начинается с Постановления Совета Министров от 25 ноября 1999 года об образовании Государственного нефтяного концерна "Нефть", преобразованного Постановлением Правительства уже РФ № 229 от 17 апреля 2000 года во всемирно известное сегодня акционерное общество.
Предприятие активно развивает разведку и добычу нефти и газа, производство и реализацию нефтепродуктов. ОЙЛ является крупнейшей в мире частной нефтяной компанией по доказанным запасам сырой нефти. Интересы компании широко представлены в странах СНГ, Восточной Европе и на Ближнем Востоке. При этом она играет ключевую роль в топливно-энергетическом секторе нашей экономики. Холдинг добывает седьмую часть всей российской нефти.
Ценные бумаги общества котируются на ведущих биржах мира. Компания выпустила в свободное обращение более 60% уставного капитала. Акции «ОЙЛа» занимают одно из ведущих мест по ликвидности на российском и международном рынке.
Официальный веб-сайт - www.oil.ru.
Задание №2. Построение и анализ линии тренда, выбранной на основе задания 1.
Построить уравнение парной регрессии (линии тренда), заполнить все приведенные ниже таблицы и построить графики.
Ваше уравнение регрессии имеет вид: Y = f(t).
1. Линеаризовать уравнение Y = f(t)заменой переменных ( для экспоненциальной 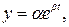
Прологарифмировать и сделать замену 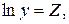
Линеаризованное уравнение будет иметь вид
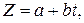
для логарифмической 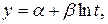
сделать замену 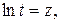
Линеаризованное уравнение будет иметь вид
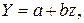
для полиноминальной 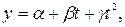
сделать замену 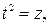
Линеаризованное уравнение будет иметь вид
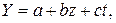
для степенной 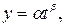
Прологарифмировать и сделать замену 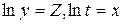
Линеаризованное уравнение будет иметь вид
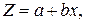
2. По линеаризованной линии тренда заполнить все приведенные ниже 4 таблицы и построить 2 графика.
Таблица 1
| Регрессионная статистика | |
| Множественный R | коэффициент корреляции r |
| R-квадрат | SS1/( SS1 + SS2) |
| Нормированный R-квадрат | R2-k(1- R2)/ (n-k-1) |
| Стандартная ошибка | (SS2/(n-k-1))^0.5 |
| Наблюдения | N=n |
Таблица 2
| df | SS | MS | F | Значимость F | |
| Регрессия | k | SS1 | SS1/k | Fвыч | α |
| Остаток | n-k-1 | SS2 | SS2/(n-k-1) | ||
| Итого | n-1 | SS1 + SS2 |
Таблица 3
| Коэффициенты | Стандартная ошибка | t-статистика | P значение | Нижние 95% | Верхние 95% | |
| Y-пересечение | a | c.o.(a) | a / c.o.(a) | 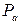 | a – tтаб * c.o.(a) | a + tтаб*c.o.(b) |
| Переменная X 1 | b | c.o.(b) | b / c.o.(b) | 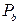 | b – tтаб * c.o.(b) | b + tтаб*c.o.(a) |
| ВЫВОД ОСТАТКА |
Таблица 4
| Наблюдение | Предсказанное Y | Остатки |
| a + b*1 | Y1 - a –b*1 | |
| a + b*2 | Y2 - a – b*2 | |
| a + b*3 | Y3 - a – b*3 | |
| … | … | … |
| n | a + b*n | Yn – a - b*n |
Замечание 1. c.o.(a)= (S2u/n(1+ 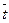 2 / σ2t))0,5, c.o.(b)= (S2u/(n σ2t))0,5,
2 / σ2t))0,5, c.o.(b)= (S2u/(n σ2t))0,5,
Где S2u=n σ2e/(n-2).
Замечание 2. Величина α в таблице 2 вычисляется с помощью функции FРАСП.
Замечание 3. Величины 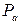 ,
, 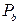 в таблице 3 вычисляется с помощью функции СТЬЮДРАСП.
в таблице 3 вычисляется с помощью функции СТЬЮДРАСП.
Замечание 4. Величина tтаб в таблице 3 вычисляется с помощью функции СТЬЮДРАСПОБР.
3. На основе таблиц 2,3 сделать обоснование адекватности уравнения опытным данным.
4. Построить графики подбора и остатков.
5. По опытным данным с помощью «Данные» Þ «Анализ данных»Þ «Регрессия» построить уравнение регрессии. Сравнить данные полученные в таблице с компьютерной выдачей.
Задание №3. Анализ остатков.
1. По линии тренда из задания №2 посчитать прогнозные значения для всех 360-365 дней.
2. Вычислить погрешность (ошибку) прогноза на каждый день.
3. Проверить ошибки на нормальность, пользуясь критерием Пирсона, по следующей методике:
· Весь диапазон наблюдений разбить на не менее, чем k = 3,22*ln (n) +1 равный интервал (число интервалов должно быть целое число!), n – число наблюдений.
· Определим крайние точки интервалов и их средины в порядке возрастания
· Подсчитаем, число попавших в каждый интервал точек, используя функцию ЧАСТОТА.
· Построим таблицу
| Границы интервала | Средины интервала | Практические частоты | Теоретические частоты |
Теоретические частоты ni* вычисляются по следующей формуле
ni* = nhφ(Si*),
φ(Si*) ={ exp [ - (Si* - a)2/(2σ2)] }/(2πσ2)0,5
где a среднее значение всей выборки остатков, σ2 выборочная дисперсия всей выборки остатков, Si*средина интервала i- го интервала, h длина интервала.
· Проверить полученную выборку на «нормальность» по критерию
Пирсона: χ2 =∑( ni*- ni)2/ (ni*)
Результат сравниваем с табличным значением , которое можно найти с помощью функции ХИ2ОБР с уровнем значимости 0,95.
· Построить на одном графике теоретические и практические частоты ( для их визуального сравнения).
· Вычислить асимметрию A и эксцесс E для массива ошибок из n данных и сделать по ним заключение о «нормальности» распределения.
Если распределение нормально, то должны выполняться одновременно неравенства:
│A│< 1,5 σA, │E + 6/(n+1)│< 1,5 σE, где
σ2A = 6(n-2)/((n+1)(n+3)), σ2E = 24n(n-2) (n-3),/((n+1)2(n+3)( n+5)).
4. Написать отчет по проведенной работе.
Задание №4. Тестирование автокорреляции и построение уравнения автокорреляции остатков
1) По тесту Дарбина –Уотсона выяснить имеет ли место автокорреляция остатков первого порядка с достоверностью 0,95.
d = =∑( ei-1- ei)2/( ∑ (ei)2)
Если автокорреляция первого порядка есть, то избавиться от нее построением уравнения вида 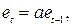
2) Проанализировать полученные остатки на автокорреляцию второго, третьего и т.д. порядков.
3) Если автокорреляция высших порядков есть, то избавиться от нее построением уравнения скользящего среднего
4) Объяснить причину возникновения автокорреляции с точки зрения экономики. Объяснить, как можно избавиться от автокорреляции с помощью сезонной составляющей или построением регрессии скользящего среднего.
5) Пишется отчет с Это делается на основе заданий №№1-4.
Пример отчета по выполненной работе.
Эконометрический анализ цен на молоко.
Белоногова М. М.,
Моделируются средние потребительские цены на молоко за 1л в Красноярском крае по 360 данным временного ряда с 01.02.2013 по 26.01.2013. В процессе подбора наиболее подходящей оказалась полиномиальная линия тренда второй степени. Все коэффициенты этого уравнения статистически значимы. Уравнение адекватно опытным данным. Остатки гомоскедастичны. Построенная модель позволяет делать прогноз на 6 месяцев с ошибкой не превышающей 5%.
Econometric analysis of milk prices.
Belonogova MM,
In this article we model of average consumer prices for milk per 1 liter in the Krasnoyarsk region of 360 time series data from 01.02.2013 on 01.26.2013. In the process of selecting the most suitable proved to be polynomial trend line of the second degree. All the coefficients of this equation are statistically significant. Equation is adequate to experimental data. Remains are homoscedasticity. The constructed model allows prediction for 6 months with an error not exceeding 5%.
Для анализа были взяты данные о цене 1 л молока (еженедельные средние потребительские цены на молоко питьевое цельное пастеризованное 2,5-3,2% жирности) в Красноярском крае за 2013 год с сайта Росстата [1].
Была получена следующая итоговая статистика:
Средняя цена 1 л молока в 2013 г. была равна 37,53 руб., стандартная ошибка средней - 7 копеек. Наиболее часто встречающаяся цена - 37,17 руб. Стандартное отклонение показывает разброс данных относительно среднего значения, т. е. цена колеблется в среднем в пределах от 36,11 до 38,94 руб. Наименьшая цена за этот период равна 36,08 руб., а наибольшая - 40,99 руб. Цена выросла в среднем почти на 5 руб.
Асимметрия показывает несимметричность распределения величины, а так как этот показатель положителен и больше 0,5, значит, асимметричность данных значительна и есть правосторонняя асимметрия. Эксцесс - положителен и близок к нулю, значит, кривая распределения близка к нормальной и расположена чуть выше.
Коэффициент вариации для данных равен 3,77%, что говорит об однородности данных, т. е. разброс данных относительно средней невелик.
Данные были разбиты на 9 групп с длиной интервала = 0,546, и была построена гистограмма частот.
График частот показывает, что большая часть данных (238) находится ниже 37,17 руб. Это значит, что почти две трети года цена за 1 л молока была ниже 37,17 руб.
Наблюдается тенденция цен к росту, то есть незначительные понижения цены были, но в целом цена на молоко повышается. Особенно заметен рост цен в конце года начиная с сентября. Такая динамика цен объясняется тем, что стоимость молока от сельхозпроизводителей с сентября – в данном случае примерно с 35 недели, или 245 дня - обычно растет, так как объем производства молока зимой гораздо меньше, чем летом.
По данным были построены разные линии тренда.
С экономической точки зрения более подходящей для прогноза будет линия полиномиальная 2-й или 3-й степени, так как линия тренда 4-й и выше степеней спускается вниз, что маловероятно для цен на молоко.
Быстрота роста цен на молоко не соответствует линии 3-й степени и маловероятно, что цена поднимется выше 46-47 рублей за литр в 2014 году, если считать, что за 2013 год цена по данным поднялась примерно на 5 рублей. Таким образом, для прогноза цены подходит больше линия 2-й степени.
Полученное уравнение регрессии для полиномиальной линии 2-й степени:
у = 36,65 - 0,0096*t + 0,0000591*t2.
Данное уравнение описывает 96,44% данных и адекватно опытным данным/ Все коэффициенты значимы Множественный R = 0,98, т. е. существует сильная связь между ценой молока и номером дня. Остатки гомоскедастичны.
Полученные остатки регрессии были проверены на автокорреляцию. Была выявлена автокорреляция первого порядка (последующая цена на молоко сильно зависит от предыдущей), коэффициент корреляции равен 0,95.
Полученная регрессия для остатков: et = 0,94720 * et-1.
Уравнение описывает 90,57% данных. Уравнение адекватно опытным данным. Коэффициент значимый. Остатки гомоскедастичны.
Остатки уравнения регрессии остатков были проверены на автокорреляцию, вывод - нет автокорреляции. Автокорреляция остатков устранена, и полученное уравнение можно использовать для прогноза.
Окончательное уравнение регрессии:
Уt = 36,66 - 0,0096*t + 0,00006* t2 + 0,94720*e t-1.
Был сделан прогноз цен на молоко (фактические значения цен на молоко в 2014 году взяты по данным Росстата) [1]:
Уравнение регрессии можно использовать для прогнозирования, пока ошибка прогноза не превышает 5%. Таким образом, полученное уравнение регрессии позволило сделать прогноз на 189 дней (6 месяцев).
Однако, так как цена за рассмотренный период колеблется незначительно, наибольшая ошибка при прогнозе не должна превышать 0,5-1 рубля – в этом случае ошибка будет составлять примерно 1-2%. 5 % - в нашем случае это более 2 рублей – слишком большая ошибка. Поэтому следует ограничить использование данного уравнения для прогноза до 153 дня (5 месяцев), где ошибка будет составлять менее 1 рубля, а для большей точности (ошибка менее 0,5 рублей) до 50 дня.
Полученное уравнение регрессии не учитывает влияние инфляции на цены. А так как в 2013 году инфляция составила 6,5%, необходимо привести цены к одному периоду (декабрю 2012 года) и строить регрессию не по фактическим ценам, а по ценам, пересчитанным с учетом инфляции. Имея средние ежемесячные цены и информацию об инфляции за каждый месяц (в % к декабрю предыдущего года) и индекс потребительских цен на товары и услуги по Красноярскому краю (в % к декабрю предыдущего года) [2], получим пересчитанные цены на молоко в ценах декабря 2012 г.:
Так как для анализа использовали данные о ценах по Красноярскому краю, то точнее будет расчет цен с учетом ИПЦ по Красноярскому краю. Полученные цены, пересчитанные с учетом инфляции и ИПЦ, более явно отражают сезонное изменение цен на молоко: до мая цена почти не меняется, падение цен в июне и значительный рост цен начиная с сентября, что обусловлено динамикой цен на молоко от сельхозпроизводителей.
