Задача на безусловный экстремум функционала
Эту задачу отличает отсутствие всяких ограничений, что является недостатком, так как отсутствие ограничений обычно лишает задачу практического смысла. Итак, задан минимизируемый функционал
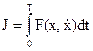 .
.
Подынтегральная функция F в нем дифференцируема как по х, так и по 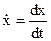 . Требуется найти экстремаль
. Требуется найти экстремаль 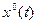 , которая минимизирует данный функционал при заданных краевых условиях x(0), х(Т) и известном значении времени Т.
, которая минимизирует данный функционал при заданных краевых условиях x(0), х(Т) и известном значении времени Т.
Идея вывода расчетного уравнения использует предположение о том, что к экстремали добавляется дополнительная функция 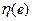 с весовым коэффициентом
с весовым коэффициентом 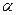 . В результате аргумент функционала получает вариацию и будет равен:
. В результате аргумент функционала получает вариацию и будет равен:
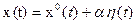 ,
,
Где 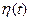 - дифференцируемая функция с нулевыми краевыми значениями, т.е.
- дифференцируемая функция с нулевыми краевыми значениями, т.е. 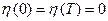 , (рис. 3).
, (рис. 3).
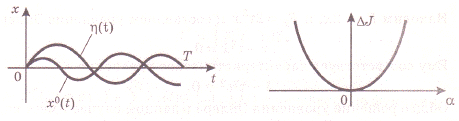
Рис. 3. Рис. 4
Соответственно функционал получает положительное приращение (вариацию), являющееся функцией коэффициента 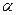 :
:

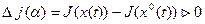 .
.
Эта функция имеет экстремум - минимум при 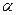 = 0 (рис.
= 0 (рис.  4). Исследуя эту функцию на экстремум, Эйлер получил следующее дифференциальное уравнение для нахождения экстремалей:
4). Исследуя эту функцию на экстремум, Эйлер получил следующее дифференциальное уравнение для нахождения экстремалей:
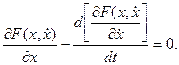
Компактная условная запись этого уравнения имеет вид:
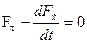 ,
,
где индексы обозначают производные по 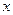 и
и 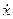 .
.
Уравнение Эйлера в общем случае является нелинейным уравнением второго порядка, общее решение которого содержит две постоянные интегрирования, определяемые из краевых условий.
В задаче на безусловный экстремум может быть задан функционал, зависящий от нескольких функций и их первых производных:


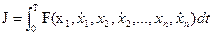 ,
,
В этом случае необходимо решить систему уравнений Эйлера:
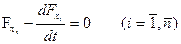 .
.
В более общем случае функционал может зависеть и от производных высших порядков. В этом случае вместо уравнений Эйлера составляют и решают уравнения Эйлера-Пуассона:
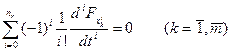 ,
,
где k- порядковый номер функции; пk - порядок старшей произ-
водной от хk; т - число функций.
Лекция 3.
1.6. Задача на условный экстремум.
Метод Эйлера-Лагранжа
Помимо минимизируемого функционала
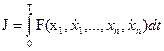 ,
,
подынтегральная функция которого зависит от нескольких функций и их первых производных по времени, задано произвольное число классических ограничений:
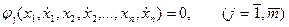 .
.
Требуется найти n экстремалей 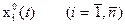 при заданных краевых условиях.
при заданных краевых условиях.
Метод решения этой задачи требует формирования нового функционала
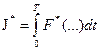 ,
,
где 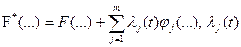 - неизвестные функции, называемые множителями Лагранжа.
- неизвестные функции, называемые множителями Лагранжа.
Благодаря такой замене задача сводится к предыдущей. При этом уравнения Эйлера должны быть составлены как для искомых экстремалей, так и для множителей Лагранжа:
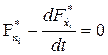 ,
, 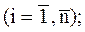 (1)
(1)
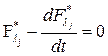 ,
, 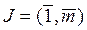 (2)
(2)
Но 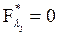 , а
, а 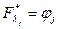 , т. е. уравнения (2) совпадают с уравнениями ограничений. Поэтому может быть выполнено совместное решение системы уравнений Эйлера (1) и заданных ограничений. Исключая время из уравнений экстремалей, можно найти алгоритм управления оптимального автоматического регулятора.
, т. е. уравнения (2) совпадают с уравнениями ограничений. Поэтому может быть выполнено совместное решение системы уравнений Эйлера (1) и заданных ограничений. Исключая время из уравнений экстремалей, можно найти алгоритм управления оптимального автоматического регулятора.
1.7. Изопериметрическая задача
Здесь наряду с ограничениями, принятыми в главе 1.6, имеется определенный интеграл по времени:
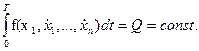
Для того чтобы эту задачу свести к предыдущей, вводим дополнительную переменную, определяемую интегральным уравнением
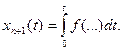
Для новой переменной справедливы краевые условия
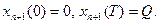
Затем, дифференцируя по времени интегральное уравнение для новой переменной, получим 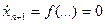 , или в стандартной форме записи ограничений:
, или в стандартной форме записи ограничений:
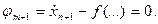
Подынтегральная функция нового функционала
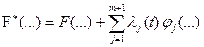 .
.
Уравнение Эйлера для новой переменной примет вид:
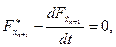
где 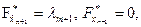 и даст результат
и даст результат 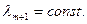
В этом и состоит особенность интегрального ограничения: множители Лагранжа для интегральных ограничений постоянны. В остальном решение аналогично, т. е. уравнения Эйлера для искомых экстремалей решаются совместно с уравнениями всех ограничений. При этом новую переменную хп+1 можно не вводить, считая 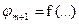 .
.
Данная задача при одном интегральном ограничении получила название изопериметрической задачи, так как исторически в этой задаче требовалось найти уравнение линии постоянного периметра, которая вместе с отрезком прямой, соединяющим данные точки, ограничивала бы максимальную площадь на плоскости. Такой линией является дуга окружности.
Лекция 3.
1.8. Принцип оптимальности. Метод динамического программирования
В основу метода динамического программирования положен принцип оптимальности. Согласно ему любой конечный отрезок оптимальной траектории (от произвольной промежуточной точки до одной и той же конечной точки процесса) является сам по себе оптимальной траекторией для своих краевых условий. Для доказательства предположим, что при движении по оптимальной траектории М0М1М2О (рис. 6) достигается минимум заданного критерия оптимальности.
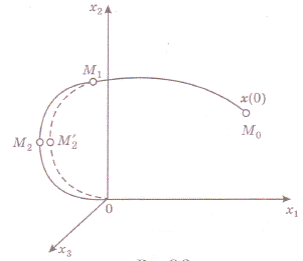
Рис.6
Докажем, что конечный отрезок М1 М2 0 является оптимальной траекторией для своих краевых условий. Допустим, что это не так, и минимум критерия оптимальности достигается при движении по траектории М1 М'20. Но тогда и при движении из точки М0 меньшее значение критерия будет получено на траектории М0 М1 М2' О, что противоречит первоначальному предположению и заставляет отвергнуть сделанное допущение.
Метод динамического программирования позволяет решать задачи трех видов: дискретную, дискретно-непрерывную и непрерывную.
1. Дискретная задача. Она отличается дискретностью всех величин (времени, управляющих воздействий, управляемых величин). К числу исходных данных относятся:
а) состояния выхода объекта управления;
б) значения управляющих воздействий;
в) алгоритм перехода из предыдущего состояния в последующее:
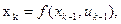
где k - номер шага, k = 1,N, причем эти переходы задаются таблицей или диаграммой переходов;
г) начальное состояние х0 и число шагов процесса N;
д) критерий оптимальности j, зависящий от состояний и управлений в оптимальном процессе.
Пусть для примера выходная величина объекта может иметь четыре состояния: х = {а1,а2,а3,а4}. Управляющее воздействие может иметь два значения: и = {-1, 1}. Диаграмма переходов показана на рис. 7. Примем х0 = a1, N = 2.
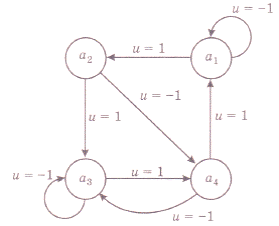
Рис. 7.
Критерий оптимальности управления объектом примем в виде функции от конечного состояния объекта 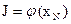 , которая задана таблично (табл. 1) и должна быть минимизирована.
, которая задана таблично (табл. 1) и должна быть минимизирована.
Таблица 1.
| xN | а 1 | а2 | а3 | a4 |
| J |
Для решения задачи около каждого конечного состояния х2
на диаграмме оптимальных переходов (рис. 8) записываем в соответствии с таблицей значения критерия оптимальности J.
Затем рассматриваются все возможные переходы из каждого предыдущего состояния х1 в последующие х2. Из них выбираются только те, которые оптимальны в смысле минимума J. Эти переходы отмечаются стрелками, около которых ставятся соответствующие
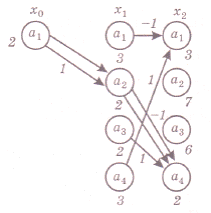
Рис. 8
значения управления, а около предшествующего состояния указывается значение J . После этого находится аналогично, оптимальный переход из начального состояния x0 в x1 Оптимальная траектория обозначена двойными стрелками и получается при управлении
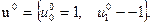
Лекция 4.
2. Дискретно-непрерывная задача МДП.
В этой задаче управляющее воздействие и управляемые величины могут иметь бесчисленное количество значений в пределах заданных ограничений. Время изменяется дискретно с малым шагом 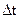 , что соответствует численным методам решения задач на ЭВМ. Задана продолжительность процесса Т, уравнение объекта управления
, что соответствует численным методам решения задач на ЭВМ. Задана продолжительность процесса Т, уравнение объекта управления
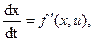 (4)
(4)
Ограничение на управление 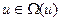 и начальное состояние x(0)=x0.
и начальное состояние x(0)=x0.
Задан в виде функционала минимизируемый критерий оптимальности
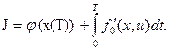 (5)
(5)
Требуется найти оптимальные управление u0(t) и траекторию x0(t).
Прежде всего от дифференциального уравнения (4) переходим к разностному уравнению, заменяя dх на хк+1- хк, dt на 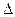 t, х и и на xk и uk, где
t, х и и на xk и uk, где 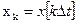 ,
, 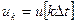 , относительное дискретное время k=0,1,2, ....
, относительное дискретное время k=0,1,2, ....
Обозначив 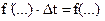 , получим из (4) разностное уравнение
, получим из (4) разностное уравнение
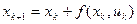 . (6)
. (6)
Критерий оптимальности (5) вместо интеграла необходимо представить в виде конечной суммы
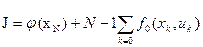 , (7)
, (7)
где 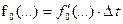 .
.
Переход к уравнениям (6) и (7) означает дискретизацию задачи по времени.
В соответствии с принципом оптимальности последовательно оптимизируем конечные отрезки процесса, начинающиеся от конечной точки t=T и постепенно увеличивающиеся на 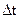 (рис.9).
(рис.9).
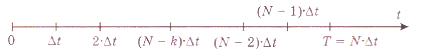
Рис. 9
Первым рассматриваем отрезок
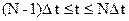 .
.
На этом отрезке из всего функционала (7) минимизируется частичная сумма
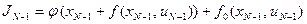
за счет изменения управления с учетом ограничений, где хN заменено согласно (6). В результате минимизации получаем следующую функцию от состояния xN-1:
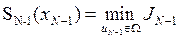 , (8)
, (8)
Данную зависимость необходимо запомнить до получения аналогичной функции на следующем шаге расчета. Кроме (8) определится и оптимальное управление
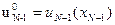 . (9)
. (9)
Функция (9) должна храниться в памяти до окончания расчета процесса. Затем переходим к отрезку 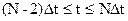 , на котором минимизируется
, на котором минимизируется
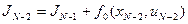 .
.
Минимум этой частичной суммы должен быть найден по двум переменным 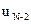 и
и 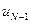 , но с учетом уже сделанной минимизации по
, но с учетом уже сделанной минимизации по 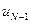 в виде (8) остается минимизировать ее только по одному аргументу
в виде (8) остается минимизировать ее только по одному аргументу 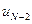 . В результате получим
. В результате получим
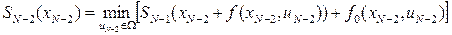 . (10)
. (10)
Функция (10) заменяет в памяти функцию (8), и находится оптимальное управление
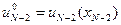 .
.
Аналогично на отрезке 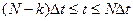 находим
находим
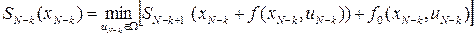 ,
,
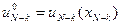 .
.
Наконец для всего процесса 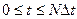 находим
находим
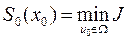 ,
,
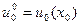 . (11)
. (11)
Таким образом, получен алгоритм расчета по рекуррентным формулам, который и называется динамическим программированием. При его применении по формуле (11) находим оптимальное управление 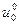 , затем по уравнению объекта (6) находим состояние объекта х1, далее находим
, затем по уравнению объекта (6) находим состояние объекта х1, далее находим 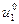 и т. д., вплоть до
и т. д., вплоть до 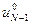 .
.
3. Непрерывная задача. Задано уравнение объекта управления
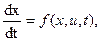 где x=[x1,…,xn]T, u=[u1,…um]T, f=[f1,…,fn]T,
где x=[x1,…,xn]T, u=[u1,…um]T, f=[f1,…,fn]T,
и краевые условия: x(t0) - закрепленный левый конец траектории, x(tf) - подвижный правый конец.
Задано ограничение на управление 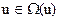 и минимизируемый функционал общего вида (функционал Больца):
и минимизируемый функционал общего вида (функционал Больца):
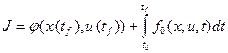 .
.
Найти оптимальное управление u0(t), траекторию x0(t) или закон оптимального управления u0=u(x, t)
Для вывода уравнения Беллмана рассмотрим две точки на искомой оптимальной траектории x(t) и x(t1) (рис. 10), причем 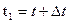 , где
, где 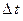 - малое приращение времени. Введем обозначение
- малое приращение времени. Введем обозначение
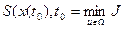 ,
,
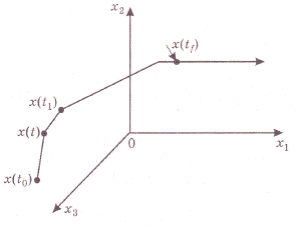
Рис. 10
которое указывает на то, что минимум критерия оптимальности зависит только от начального состояния и начального момента времени процесса. Применяя принцип оптимальности, можно выразить минимальное значение функционала для конечных отрезков траектории, начинающихся в точках х(t) и x(t1):
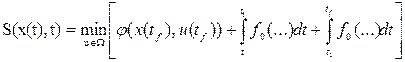 ,
,
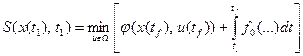 .
.
Сравнение этих равенств позволяет выразить первый минимум через второй:
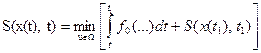 .
.
Входящий в это равенство интеграл можно заменить произведением его подынтегральной функции на 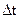 (вследствие малости последнего). Кроме того, функцию, входящую в левую часть, как независящую от управления, можно ввести под знак минимума для того, чтобы получить приращение функции S, называемой функцией Беллмана. После этого придем к следующему результату:
(вследствие малости последнего). Кроме того, функцию, входящую в левую часть, как независящую от управления, можно ввести под знак минимума для того, чтобы получить приращение функции S, называемой функцией Беллмана. После этого придем к следующему результату:
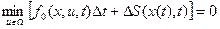 .
.
Поделив почленно равенство на 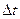 и устремив
и устремив 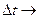 0, получим:
0, получим:
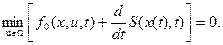 (12)
(12)
Считая функцию Беллмана S непрерывной и дифференцируемой функцией всех своих аргументов, выразим производную 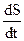 как производную сложной функции, причем производную
как производную сложной функции, причем производную 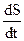 , как независящую от управления u, перенесем в правую часть равенства:
, как независящую от управления u, перенесем в правую часть равенства:
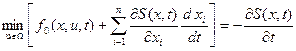 .
.
Заменив входящие сюда производные переменных состояния на соответствующие функции из уравнений объекта управления, получим уравнение Беллмана в общем виде:
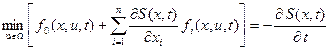 . (13)
. (13)
Применяется и другая запись уравнения Беллмана с использованием скалярного произведения, в которое входит градиент функции S:
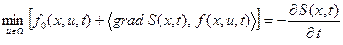 . (14)
. (14)
В частном случае, когда объект стационарен и подынтегральная функция функционала f0 не зависит от времени, искомая функция Беллмана S также не будет явно зависеть от времени.
Следовательно, 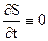 и уравнение Беллмана упрощается, что соответствует так называемой задаче Лагранжа:
и уравнение Беллмана упрощается, что соответствует так называемой задаче Лагранжа:
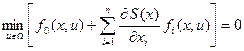 . (15)
. (15)
Для задачи максимального быстродействия 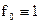 , и уравнение Беллмана (15) приобретает вид:
, и уравнение Беллмана (15) приобретает вид:
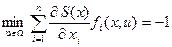 . (16)
. (16)
Из уравнения Беллмана должна быть найдена функция Беллмана S и оптимальное управление, что на практике выполняется в следующем порядке при оптимизации обобщенного квадратичного функционала.
1. В соответствии с исходными данными выбираем то или иное уравнение Беллмана (13)-(16).
2. Минимизируем по управляющему воздействию и левую часть уравнения Беллмана, выражая при этом искомое оптимальное управление через производные неизвестной функции S.
3. Подставляем в уравнение Беллмана найденное выражение для оптимального управления. При этом знак min опускается.
4. Решаем полученное уравнение относительно функции Беллмана S. Решение ищется в виде положительно определенной квадратичной формы 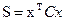 . После подстановки выражения для функции S в уравнение Беллмана элементы симметричной матрицы С могут быть найдены приравниванием к 0 всех коэффициентов квадратичной формы, образовавших левую часть уравнения Беллмана.
. После подстановки выражения для функции S в уравнение Беллмана элементы симметричной матрицы С могут быть найдены приравниванием к 0 всех коэффициентов квадратичной формы, образовавших левую часть уравнения Беллмана.
5. Подставляем функцию Беллмана, как функцию переменных состояния, в выражение для оптимального управления, найденного в п. 2. В результате получим оптимальный алгоритм управления. Соответствующая система устойчива, так как удовлетворяет требованиям прямого метода Ляпунова. Действительно, приняв функцию Беллмана за функцию Ляпунова, т. е. Считая S=V, получаем 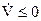 согласно (12) при положительной определенности f0(х, и, t).
согласно (12) при положительной определенности f0(х, и, t).
Лекция 5.
Принцип оптимальности. Метод динамического программирования
Принцип максимума
Это метод расчета оптимальных процессов и систем, который выражает необходимое условие оптимальности. Рассмотрим упрощенный вывод принципа максимума.
Задано уравнение управляемого объекта в векторно-матричной форме
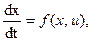
где 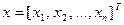 .
.
Ограничение наложено на скалярное управляющее воздействие 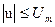 .
.
Задан минимизируемый функционал:
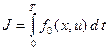 .
.
Необходимо найти оптимальные управление 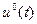 и траекторию
и траекторию 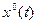 . Порядок решения поставленной задачи следующий.
. Порядок решения поставленной задачи следующий.
1. Вводим дополнительную переменную состояния
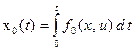 ,
,
конечное значение которой 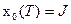 , т.е. равно критерию оптимальности. Эта переменная вместе с другими характеризует объект управления и образует обобщенный вектор состояния
, т.е. равно критерию оптимальности. Эта переменная вместе с другими характеризует объект управления и образует обобщенный вектор состояния
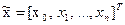 .
.
Дифференцируя по t выражение для новой переменной найдем уравнение в нормальной форме 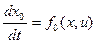 . Добавив это уравнение в систему заданных уравнений объекта управления, получим систему обобщенных уравнений:
. Добавив это уравнение в систему заданных уравнений объекта управления, получим систему обобщенных уравнений:
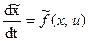 , (17)
, (17)
где 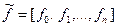 .
.
2. Производим игольчатую вариацию управляющего воздействия относительно искомого оптимального закона его изменения (рис. 12), при которой это воздействие скачком изменяется до предельного значения и затем обратно в течение бесконечно малого отрезка времени 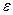 .
.
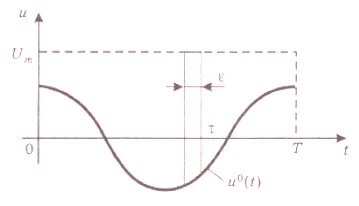
Рис. 12
Площадь игольчатой вариации бесконечно мала, поэтому она вызывает бесконечно малые отклонения (вариации) переменных состояния:
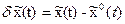 ,
,
где 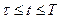 .
.
В частности, вариация
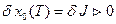 , (18)
, (18)
так как система оптимальна по минимуму критерия оптимальности.
3. Выразим вариацию траектории в момент времени 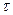 как произведение ее скорости на длительность вариации, т. е.
как произведение ее скорости на длительность вариации, т. е.
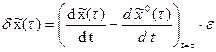 .
.
В последнем равенстве заменим скорости на соответствующие функции, взятые из (17):
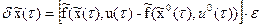 . (19)
. (19)
4. Определим вариацию критерия оптимальности в момент 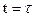 по формуле скалярного произведения:
по формуле скалярного произведения:
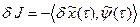 , (20)
, (20)
где 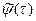 - вспомогательная вектор-функция, подлежащая определению и имеющая смысл градиента изменения критерия оптимальности при изменении переменных состояния.
- вспомогательная вектор-функция, подлежащая определению и имеющая смысл градиента изменения критерия оптимальности при изменении переменных состояния.
5. Подставляем (19) в (20) и с учетом знака вариации 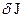 получим неравенство для
получим неравенство для 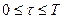 :
:
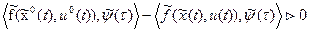 . (21)
. (21)
6. Обозначаем функцию Гамильтона (гамильтониан)
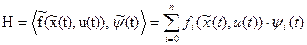 . (22)
. (22)
Сравнение (22) и (21) позволяет сформулировать принцип максимума.
Для оптимального управления объектом необходимо, чтобы гамильтониан Н имел максимальное (наибольшее) значение в любой момент процесса управления.
Если оптимальное управление находится внутри допустимой области, то гамильтониан Н достигает максимума. Если же управление 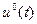 меняется по границам этой области, то Н достигает своего наибольшего значения (супремума).
меняется по границам этой области, то Н достигает своего наибольшего значения (супремума).
7. Для нахождения вспомогательных функций получены следующие уравнения:
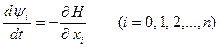 . (23)
. (23)
Для функций 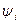 в соответствии с (20) и (18) получаются следующие граничные условия:
в соответствии с (20) и (18) получаются следующие граничные условия:
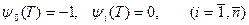 .
.
Так как гамильтониан Н от х0не зависит, то из (23) имеем 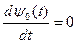 , следовательно,
, следовательно, 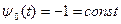 .
.
1.10. Порядок практического применения принципа максимума
1. Располагая заданным функционалом и уравнениями объекта, составляем гамильтониан Н по формуле (22). Причем, если подынтегральная функция f0 от управления и не зависит, то соответствующее слагаемое можно в гамильтониан не включать, так как это не повлияет на решение задачи. Это справедливо, в частности, для критерия максимального быстродействия, когда f0=1.
2. Исследуем гамильтониан Н на максимум по управлению и, т. е. решаем уравнение 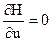 .
.
Отсюда находим в общем виде оптимальное управление через переменные 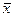 и
и 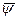 . Если это уравнение приводит к нулевым значениям хотя бы для одной функции
. Если это уравнение приводит к нулевым значениям хотя бы для одной функции 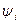 ; (тривиальное решение), то это считается неприемлемым и означает, что оптимальное управление изменяется по границам допустимой области. Соответственно гамильтониан Н имеет не максимум, а наибольшее значение (супремум). В этом случае оптимальный закон управления находится из выражения для Н в классе знаковых функций с учетом ограничений на управление.
; (тривиальное решение), то это считается неприемлемым и означает, что оптимальное управление изменяется по границам допустимой области. Соответственно гамильтониан Н имеет не максимум, а наибольшее значение (супремум). В этом случае оптимальный закон управления находится из выражения для Н в классе знаковых функций с учетом ограничений на управление.
3. Найденный оптимальный алгоритм управления подставляют в уравнения (16) и (23), и они решаются совместно. При этом решении возникают сложности с определением постоянных интегрирования, удовлетворяющих граничным условиям. Поэтому обычно ограничиваются решением качественного характера, при котором определяется лишь характер изменения оптимального управления. Дальнейшее применение метода припасовывания позволяет получить точное решение количественного характера.
Лекция 6.
1.12. Синтез оптимального по быстродействию регулятора для линейного стационарного объекта второго порядка
Этот синтез производится с использованием метода припасовывания в фазовом пространстве и теоремы об п интервалах. Объект управления задан своим дифференциальным уравнением
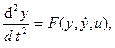 (24)
(24)
где 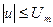 .
.
Требуется определить алгоритм оптимального управления 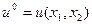 при произвольных краевых условиях.
при произвольных краевых условиях.
Порядок синтеза следующий:
1. В качестве переменных состояния целесообразно выбрать ошибку управления х1 и ее первую производную х2 по времени
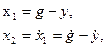
так как на фазовой плоскости этих переменных изображающая точка в конце оптимального переходного процесса приходит в начало координат.
Учитывая эти равенства и заданное уравнение объекта управления, запишем систему уравнений последнего в нормальной форме:
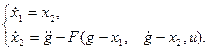 (25)
(25)
2. Определяем допустимое задающее воздействие g(t) в неко-
тором классе функций, например, в классе полиномиальных
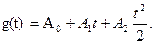 (26)
(26)
Допустимым называется такое задающее воздействие которое управляемая величина y(t) может «догнать» при заданном
ограничении на управление.
Определим, какие значения коэффициентов A0, A1 и A2 допус-
тимы при заданном ограничении. Исходим из требования, что в
конце переходного процесса ошибка и ее производные первого и
второго порядка должны равняться 0:
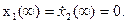 (27)
(27)
Решим эту задачу применительно к двигателю постоянного
тока как объекту регулирования угла поворота вала. Исходное
уравнение (24) и уравнения (25) примут вид:
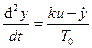 ;
;
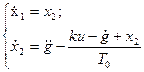 . (28)
. (28)
Требование (27) с учетом (26) и (28) можно записать в виде:
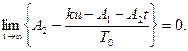
Так как функция A2t растет неограниченно, а управление и ограничено значением Um, то это равенство может быть выполнено при
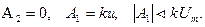
Для объектов управления с разным порядком астатизма V требования к коэффициентам А0, А1и А2сведены в табл. 2.
Таблица 2
| Порядок V | A0 | A1 | А2 |
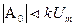 | |||
| Любое | 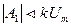 | ||
| Любое | Любое | 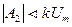 |
3. Находим дифференциальное уравнение фазовых траекторий объекта управления, решаем его и строим два семейства фазовых траекторий при 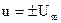 .
.
Уравнение фазовой траектории объекта при оптимальном управлении имеет общий вид
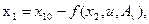 (29)
(29)
где 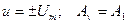 для объекта в виде двигателя постоянного тока.
для объекта в виде двигателя постоянного тока.
Постоянная интегрирования х10 имеет смысл координаты точки пересечения фазовой траектории с осью х1, так как функция f равна 0 при х2 = 0. По найденному уравнению можно построить два семейства фазовых траекторий (рис.14).
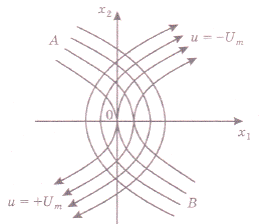
Рис. 14
4. Строим фазовый портрет оптимальной по быстродействию системы, используя теорему об п интервалах и метод припасовывания. Так как изображающая точка в конце переходного процесса должна приходить в начало координат, то второй интервал оптимального процесса должен совершаться по отрезкам нулевых полутраекторий АО или ВО.
Первый интервал того же процесса должен совершаться по полутраекториям семейства 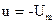 , оканчивающимся на АО, либо по полутраекториям
, оканчивающимся на АО, либо по полутраекториям 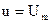 , оканчивающимся на ВО (рис.15).
, оканчивающимся на ВО (рис.15).
5. Используя построенный фазовый портрет, синтезируем алгоритм оптимального по быстродействию регулятора.
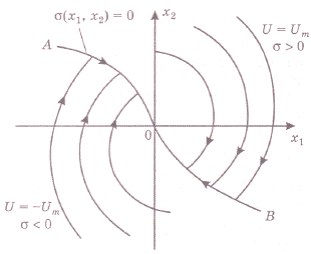
Рис.15
Из фазового портрета видно, что оптимальный регулятор является релейным двухпозиционным, и его линия переключения (ЛП) - это АОВ. Найдем ее уравнение. Для этого нужно учесть, во-первых, общее уравнение фазовых траекторий (29), во-вторых, прохождение линии АОВ через начало координат, т. е. х10 = О, в-третьих, то, что на линии АОВ управление u совпадает по знаку с переменной х2, т. е. 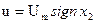 . Перенеся все члены уравнения (29) в одну часть, запишем уравнение ЛП
. Перенеся все члены уравнения (29) в одну часть, запишем уравнение ЛП
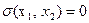 ,
,
где 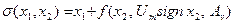 . (30)
. (30)
Функция 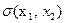 является функцией переключения регулятора, так как она совпадает по знаку с оптимальным управлением на всей фазовой плоскости, кроме линии АОВ (рис.15).
является функцией переключения регулятора, так как она совпадает по знаку с оптимальным управлением на всей фазовой плоскости, кроме линии АОВ (рис.15).
Итак, алгоритм работы оптимального регулятора на первом интервале управления
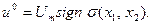 (31)
(31)
 Заметим, что равенства (30) и (31) определяют алгоритм работы оптимального регулятора приближенно, т. е. в квазиоптимальном режиме. Приближенность состоит в том, что второй интервал процесса при таком алгоритме управления будет совершаться не по отрезкам АО и ВО, а по бесконечно близким отрезкам фазовых траекторий, получающимся после пересечения ЛП изображающей точкой.
Заметим, что равенства (30) и (31) определяют алгоритм работы оптимального регулятора приближенно, т. е. в квазиоптимальном режиме. Приближенность состоит в том, что второй интервал процесса при таком алгоритме управления будет совершаться не по отрезкам АО и ВО, а по бесконечно близким отрезкам фазовых траекторий, получающимся после пересечения ЛП изображающей точкой.
В соответствии с выражениями (30) и (31) построим структурную схему оптимальной по быстродействию системы автоматического управления объектом с астатизмом первого порядка (рис.16).
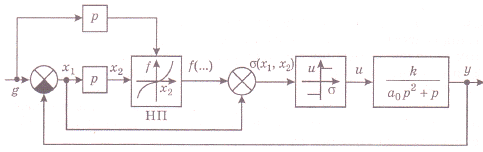
Рис.16
1.13. Оптимальные по быстродействию процессы
при ограничениях на управление
и одну из производных регулируемой величины
Рассмотрим в общем виде оптимальный по быстродействию процесс управления объектом п-го порядка с уравнением
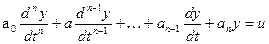
при двух ограничениях:
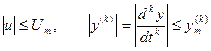 .
.
Анализ оптимального процесса показывает, что он состоит из нескольких участков:
1) участок перевода ограниченной координаты 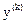 от заданного начального значения
от заданного начального значения 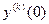 к одному из предельно допустимых значений
к одному из предельно допустимых значений 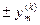 ;
;
2) участок стабилизации этой координаты на достигнутом предельно допустимом значении;
3) участок перевода ограниченной координаты от предельного допустимого значения одного знака до предельно допустимого значения противоположного знака и т. д.;
2к + 1) участок перевода 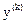 от одного из предельно допустимых значений до конечного значения
от одного из предельно допустимых значений до конечного значения 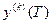 .
.
Всего в процессе имеется kучастков стабилизации и k+ 1 участок перевода. Причем каждый участок перевода математически описывается уравнением, получаемым из уравнения объекта, если выходом считать не величину у, а ее k-ю производную y(k). При этом порядок уравнения понижается и становится равным n-k. Если соответствующее характеристическое уравнение 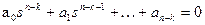 удовлетворяет теореме об n интервалах, то в соответствии с этой теоремой на каждом участке перевода имеем n-k интервалов с постоянными управляющими воздействиями на уровнях
удовлетворяет теореме об n интервалах, то в соответствии с этой теоремой на каждом участке перевода имеем n-k интервалов с постоянными управляющими воздействиями на уровнях 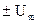 .
.
Каждый участок стабилизации описывается заданным уравнением объекта, в котором производная k-го порядка постоянна. Поэтому производные высшего порядка от k+1 до n равны 0. В результате интегрирования можно найти младшие производные и выходную величину объекта управления. Затем из уравнения объекта можно найти управляющее воздействие на участке стабилизации как функцию времени. Этот закон изменения управления 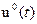 будет непрерывным и может быть обеспечен либо в разомкнутой системе заданием программы, либо в замкнутой системе за счет нелинейной отрицательной обратной связи по производной y(k) которая называется отсечкой. Такая отрицательная обратная связь не проявляет себя, пока не достигнуто ограничение, и имеет бесконечно большой коэффициент усиления в обратном случае.
будет непрерывным и может быть обеспечен либо в разомкнутой системе заданием программы, либо в замкнутой системе за счет нелинейной отрицательной обратной связи по производной y(k) которая называется отсечкой. Такая отрицательная обратная связь не проявляет себя, пока не достигнуто ограничение, и имеет бесконечно большой коэффициент усиления в обратном случае.
Лекция 7.
