Вращение твердого тела вокруг неподвижной оси

Угол поворота, угловая скорость и угловое ускорение

Вращением твердого тела вокруг неподвижной оси называ­ется такое его движение, при котором две точки тела остаются неподвижными в течение всего времени движения. При этом также остаются неподвижными все точки тела, расположенные на прямой, проходящей через его неподвижные точки. Эта прямая называется осью вращения тела.

Если А и В — неподвижные точки тела (рис. 15), то осью вращения является ось Oz, которая может иметь в пространстве любое направление, не обязательно вертикальное. Одно на­правление оси Oz принимается за положительное.

Через ось вращения проведем неподвижную плоскость П_о и подвижную П, скрепленную с вращающимся телом. Пусть в начальный момент времени обе плоскости совпадают. Тогда в момент времени t положение подвижной плоскости и самого вращающегося тела можно определить двугран­ным углом между плоскостями и соответствующим линейным углом φ между прямыми, расположенными в этих плоскостях и перпендикулярными оси вращения. Угол φ называется углом поворота тела.

Положение тела относительно выбранной системы отсчета полностью определяется в любой

момент времени, если задано уравнение φ = f(t) (5)

где f(t) — любая, дважды дифференцируемая функция времени. Это уравнение называют уравнением вращения твердого тела вокруг неподвижной оси.

У тела, совершающего вращение вокруг неподвижной оси, одна степень свободы, так как его положение определяется заданием только одного параметра — угла φ.

Угол φ считается положительным, если он откладывается против часовой стрелки, и отрицательным — в противополож­ном направлении, если смотреть с положительного направления оси Oz. Траектории точек тела при его вращении вокруг неподвижной оси являются окружностями, расположенными в плоскостях, перпендикулярных оси вращения.

Для характеристики вращательного движения твердого тела вокруг неподвижной оси введем понятия угловой скорости и углового ускорения. Алгебраической угловой скоростью тела в какой-либо момент времени называют первую производную по времени от угла поворота в этот момент, т. е. dφ/dt = φ. Она является величиной положительной при вращении тела против часовой стрелки, так как угол поворота возрастает с течением времени, и отрицательной — при вращении тела по часовой стрелке, потому что угол поворота при этом убывает.

Модуль угловой скорости обозначают ω. Тогда ω=׀dφ/dt׀=׀φ׀ (6)

Размерность угловой скорости устанавливаем в соответствии с (6)

[ω] = угол/время = рад/с = с^-1.

Втехнике угловая скорость — это частота вращения, выражен­ная в оборотах в минуту. За 1 мин тело повернется на угол 2πп, если п — число оборотов в минуту. Разделив этот угол на число секунд в минуте, получим: (7)

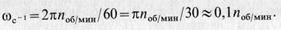
Алгебраическим угловым ускорением тела называют первую производную по времени от алгебраической скорости, т.е. вторую производную от угла поворота d²φ/dt² = ω. Модуль углового ускорения обозначим ε, тогда ε=|φ| (8)

Размерность углового ускорения получаем из (8):

[ε] = угловая скорость/время = рад/с² = с ^-2

Если φ’’>0 при φ’>0, то алгебраическая угловая скорость возрастает с течением времени и, следовательно, тело вращается ускоренно в рассматриваемый момент времени в положительную сторону (против часовой стрелки). При φ’’<0 и φ’<0 тело вращается ускоренно в отрицательную сторону. Если φ’’<0 при φ’>0, то имеем замедленное вращение в положительную сторону. При φ’’>0 и φ’<0, т.е. замедленное вращении совершается в отрицательную сторону. Угловую скорость и угловое ускорение на рисунках изображают дуговыми стрелками вокруг оси вращения. Дуговая стрелка для угловой скорости указывает направление вращения тел;

Для ускоренного вращения дуговые стрелки для угловой скорости и углового ускорения имеют одинаковые направления для замедленного — их направления противоположны.

Частные случаи вращения твердого тела

Вращение называют равномерным, если ω=const, φ= φ’t

Вращение будет равнопеременным, если ε=const. φ’= φ’₀+ φ’’t и

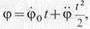
В общем случае, если φ’’ не постоянно,

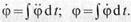
Скорости и ускорения точек тела

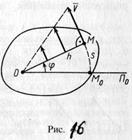
Известно уравнение вращения твердого тела вокруг непо­движной оси φ= f(t) (рис.16). Расстояние s точки М в по­движной плоскости П по дуге окружности (траектории точки), отсчитываемое от точки М_о, расположенной в неподвижной плоскости, выражается через угол φ зависимостью s=hφ, где h—радиус окружности, по которой перемещается точка. Он является кратчайшим расстоянием от точки М до оси враще­ния. Его иногда называют радиусом вращения точки. У каждой точки тела радиус вращения остается неизменным при враще­нии тела вокруг неподвижной оси.

Алгебраическую скорость точки М определяем по формуле v_τ=s’=hφ Модуль скорости точки: v=hω (9)

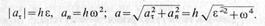
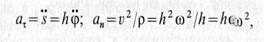
Скорости точек тела при вращении вокруг неподвижной оси пропорциональ­ны их кратчайшим расстояниям до этой оси. Коэффициентом пропорци­ональности является угловая ско­рость. Скорости точек направлены по касательным к траекториям и, сле­довательно, перпендикулярны радиу­сам вращения. Скорости точек тела, расположен­ных на отрезке прямой ОМ, в соот­ветствии с (9) распределены по линей­ному закону. Они взаимно параллельны, и их концы располагаются на одной прямой, проходящей через ось вращения. Ускорение точки разлагаем на ка­сательную и нормальную составля­ющие, т. е. a=a_τ+a _nτ Касательное и нормальное ускорения вычисляются по формулам (10)

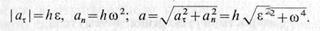
так как для окружности радиус кривизны р=h (рис. 17). Таким образом,

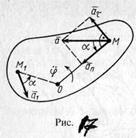Касательные, нормальные и полные ускорения точек, как и скорости, распределены тоже по линейному закону. Они линейно зависят от расстояний точек до оси вращения. Нормальное ускорение направлено по радиусу окружности к оси вращения. Направление касательного ускорения зависит от знака алгебраического углового ускорения. При φ’>0 и φ’’>0 или φ’<0 и φ’<0 имеем ускоренное вращение тела и направле­ния векторов a_τ и v совпадают. Если φ’ и φ’' имеют разные знаки (замедленное вращение), то a_τ и v направлены проти­воположно друг другу.

Обозначив α угол между полным ускорением точки и ее радиусом вращения, имеем

tgα = | a_τ |/a_n = ε/ω² (11)

так как нормальное ускорение а_п всегда положительно. Угол а для всех точек тела один и тот же. Откладывать его следует от ускорения к радиусу вращения в направлении дуговой стрелки углового ускорения независимо от направления вращения твердого тела.

Векторы угловой скорости и углового ускорения

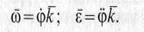
Введем понятия векторов угловой скорости и углового ускорения тела. Если К — единичный вектор оси вращения, направленный в ее положительную сторону, то векторы угловой скорости ώ и углового ускорения ε определяют выражениями (12)

Так как k—постоянный по мо­дулю и направлению вектор, то из (12) следует, что

ε=dώ/dt (13)

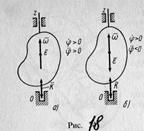
При φ’>0 и φ’’>0 направления векторов ώ и ε совпадают. Они оба направлены в положительную сторону оси вращения Oz (Рис. 18.а)Если φ’>0 и φ’’<0, то они направлены в противополож­ные стороны (рис.18.б). Вектор углового ускорения совпадает по направлению с вектором угловой скорости при ускоренном вращении и противоположен ему при замедленном. Векторы ώ и ε можно изображать в любых точках оси вращения. Они являются векторами скользящими. Это их свойство следует из векторных формул для скоростей и ускоре­ний точек тела.

Сложное движение точки

Основные понятия

Для изучения некоторых, более сложных видов движений твердого тела целесообразно рассмотреть простейшее сложное движение точки. Во многих задачах движение точки приходится рассматривать относительно двух (и более) систем отсчета, движущихся друг относительно друга. Так, движение космичес­кого корабля, движущегося к Луне, требуется рассматривать одновременно и относительно Земли и относительно Луны, которая движется относительно Земли. Любое движение точки можно считать сложным, состоящим из нескольких движений. Например, движение корабля по реке относительно Земли можно считать сложным, состоящим из движения по воде и вместе с текущей водой.

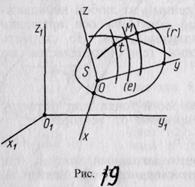
В простейшем случае сложное движение точки состоит из относительного и переносного движений. Определим эти дви­жения. Пусть имеем две системы отсчета, движущиеся друг относительно друга. Если одну из этих систем O_lx₁y₁z₁ (рис. 19) принять за основную или неподвижную (ее движение относительно других систем отсчета не рассматривается), то вторая система отсчета Oxyz будет двигаться относительно первой. Движение точки относительно подвижной системы отсчета Oxyz называется относительным. Характеристики этого движения, такие, как траектория, скорость и ускорение, назы­ваются относительными. Их обозначают индексом r; для скорости и ускорения v_r, a_r. Движение точки относительно основной или неподвижной системны системы отсчета O₁x₁y₁z₁ называется абсолютным (или сложным). Его также иногда называют составным движением. Траектория, скорость и ускорение этого движения называются абсолютными. Скорость и ускорение абсолютного движения обозначают буквами v, a без индексов.

Переносным движением точки называют движение, которое она совершает вместе с подвижной системой отсчета, как точка, жестко скрепленная с этой системой в рассматриваемый момент времени. Вслед­ствие относительного движения движущаяся точка в различные моменты времени совпадает с различными точками тела S, с которым скреплена подвижная система отсчета. Переносной скоростью и переносным ускорением являются скорость и уско­рение той точки тела S, с которой в данный момент совпадает движущаяся точка. Переносные скорость и ускорение обознача­ют v_e, а_е.

Если траектории всех точек тела S, скрепленного с подвиж­ной системой отсчета, изобразить на рисунке (рис. 20), то получим семейство линий — семейство траекторий переносного движения точки М. Вследствие относительного движения точки М в каждый момент времени она находится на одной из траекторий переносного движения. Точка М может совпадать только с одной точкой каждой из траекторий этого семейства переносных траекторий. В связи с этим иногда считают, что траекторий переносного движения нет, так как приходится считать траекториями переносного движения линии, у которых только одна точка фактически является точкой траектории.

В кинематике точки изучалось движение точки относительно какой-либо системы отсчета независимо от того, движется эта система отсчета относительно других систем или нет. Дополним это изучение рассмотрением сложного движения, в простейшем случае состоящего из относительного и перенос­ного. Одно и то же абсолютное движение, выбирая различные подвижные системы отсчета, можно считать состоящим из разных переносных и соответственно относительных движений.

Сложение скоростей

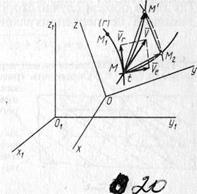
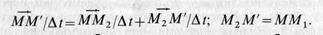Определим скорость абсолютного движения точки, если известны скорости относительного и переносного движений этой точки. Пусть точка со­вершает только одно, относи­ тельное движение по отношению к подвижной системе отсчета Oxyz и в момент времени t за­нимает на траектории относи­ тельного движения положение М (рис 20). В момент времени t+ t вследствие относительного Движения точка окажется в по­ложении М₁, совершив пере­мещение ММ₁ по траектории относительного движения. Пред­положим, что точка участвует Oxyz и относительной траекторией она переместится по некоторой кривой на ММ_2. Если точка участвует одновременно и в относительном и в переносном движениях, то за время А; она переместится на ММ' по траектории абсолютного движения и в момент времени t+At займет положение М'. Если время At мало и в дальнейшем переходят к пределу при At, стремящемся к нулю, то малые перемещения по кривым можно заменить отрезками хорд и принять их за векторы перемещений. Складывая векторные пе­ремещения, получаем

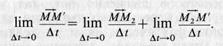В этом отношении отброшены малые величины более высокого порядка, стремящиеся к нулю при At, стремящемся к нулю. Переходя к пределу, имеем (14)

Следовательно, (14) примет форму (15)

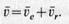
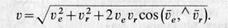Получена так называемая теорема сложения скоростей: скорость абсолютного движения точки равна векторной сумме скоростей переносного и относительного движений этой точки. Так как в общем случае скорости переносного и относительного движений не перпендикулярны, то (15’)