Многогранники і тіла обертання

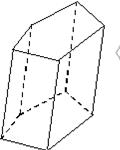Означення.п-кутна призма – многогранник, дві грані якого п-кутники, що лежать у різних площинах і суміщаються паралельним перенесенням, а інші п граней – паралелограми.

n-кутники називають основами призми, а паралелограми – бічни­ми гранями призми.

Сторони основ називають ребрами основ, інші ребра називають біч­ними ребрами.

Висота призми – відстань між площинами її основ.

Діагональ призми – відрізок, який сполучає дві вершини, що не належать одній грані.

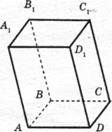
Означення. Паралелепіпед – призма, основа якої паралелограм. АВСDА₁В₁С₁D₁ – паралелепіпед.

Протилежні грані паралелепіпеда – грані паралелепіпеда, які не мають спільних вершин

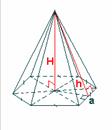
Означення.n-кутна піраміда – многогранник, у якого одна грань – довільний n-кутник, а останні n граней – трикутники, що мають спільну вер­шину, n-кутник називають основою, трикутники – бічними граня­ми, а спільну вершину бічних граней – вершиною піраміди.

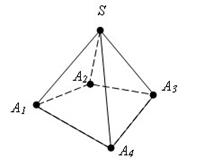
SA₁A₂A₃A₄– піраміда, A₁A₂A₃A₄ – основа; SA₁A₂, SA₂A₃, SA₃A₄, SA₁A₄ – бічні грані; S – вершина піраміди. Висота – перпендикуляр, опущений з вершини піраміди

на площину основи.

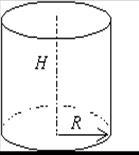Означення. Циліндром називається тіло, що складається з двох кругів, які не лежать в одній площині і суміщаються паралельним перенесенням, і всіх відрізків, що сполучають відповідні точки цих кругів. Круги називаються основами циліндра, а відрізки, що сполучають точки кіл кругів, – твірними циліндра. Відстань між площинами основ називається висотою циліндра.

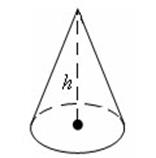
Означення. Конусом називається тіло, яке складається з круга – основи конуса, точки, яка не лежить у площині цього круга – вершини конуса і всіх відрізків, що сполучають вершину конуса з точками кола основи. Відрізки, що сполучають вершину конуса з точками кола основи, називаються твірними конуса.

Висота - перпендикуляр, опущений з вершини конуса на

площину основи.

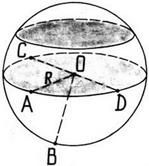
Означення. Кулею називається тіло, що складається з усіх точок простору, які знаходяться від даної точки на відстані, не більшій за дану. Ця точка називається центром кулі, а дана відстань радіусом кулі.

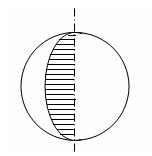
Куля є тілом обертання. Вона утворюється під час обертання півкруга навколо його діаметра як осі.

Межа кулі називається кульовою поверхнею або сферою.

Питання для самоконтролю

1. Дайте означення прямої, відрізка, променя, кута. Як вони позначаються?

2. Назвіть види кутів і дайте їм означення.

3. Якими одиницями вимірюються довжина відрізка, величина кута? Поясніть співвідношення між одиницями вимірювання.

4. Що називається многокутником? Назвіть його складові частини і дайте їм означення.

5. Дайте означення трикутника. Що називається висотою, медіаною трикутника і бісектрисами його кутів?

6. Назвіть види трикутників і їх властивості.

7. Що називається чотирикутником? Назвіть його складові.

8. Дайте означення прямокутника, паралелограма, ромба, квадрата. Назвіть спільне і відмінне цих фігур.

9. Сформулюйте властивості прямокутника, паралелограма, ромба, квадрата.

10. Що називається кругом і колом? В чому їх відмінність? Назвіть елементи і властивості цих фігур.

11. Що називається призмою? Назвіть складові елементи призми.

12. Що називається паралелепіпедом? Порівняйте паралелепіпед з призмою.

13. Що називається пірамідою? Назвіть складові елементи піраміди.

14. Назвіть відомі вам тіла обертання і дайте їм означення?

Система вправ

1. Дайте означення прямого кута. Знайдіть у підручнику математики для початкових класів вправу, в якій учні знайомляться з прямим кутом. Порівняйте означення.

2. Знайдіть у підручнику математики для початкових класів вправу, де учні знайомляться з кругом і колом. На що треба звернути увагу учнів, що вони не плутали ці поняття?

3. Дайте означення паралелограма і прямокутника. Вкажіть родове поняття і видову відмінність у кожному з означень і порівняйте їх.

4. Знайдіть у підручнику математики для початкових класів вправи, в яких розглядаються просторові тіла. Назвіть їх.

5. Побудуйте різні прямокутники, в кожному з яких периметр дорівнює 20 см (довжини сторін – натуральні числа). Скільки розв’язків має задача?

6. У підручнику математики для початкових класів знайдіть вправи, в яких геометричні фігури використовуються як об’єкти для перелічування.

7. Побудуйте чотирикутник і відрізком розбийте його на частини, щоб утворились: а) два трикутника, б) трикутник і чотирикутник, в) два чотирикутника, г) трикутник і п’ятикутник.

Література

1. Боровик В.Н., Вивальнюк Л.М., Мурач М.М., Соколенко О.І. Курс Математики. – К.: Вища школа, 1995. – 392 с.

2. Вивальнюк Л.М., Григоренко В.К., Левищенко С.С. Числові системи. – К.: Вища школа, 1988. – 272 с.

3. Кужель О.В. Елементи теорії множин і математичної логіки. –К.: Рад. шк., 1977. – 160 с.

4. Кухар В.М., Білий Б.М. Теоретичні основи початкового курсу математики. – К.: Вища школа, 1987. – 319 с.

5. Лаврова Н. Н., Стойлова Л.П. Задачник-практикум по математике. – М.: Просвещение, 1985. – 184 с.

6. Погорєлов О.В. Геометрія: Стереометрія: Підручник для 10-11 кл. серед. Шк.. – К.: Освіта, 2001. – 128с.

7. Стойлова Л.П., Пышкало А.М. Основы начального курса математики. – М.: «Просвещение», 1988. – 320 с.

Джерела інформації

1. http://uk.wikipedia.org/wiki/

2. http://testportal.if.ua/subjekt.php?tutor =196

3. http://www. terver.ru/maththeoryGeometry.php

4. http://www.pm 298. ru/mgeom.php

5. http://ru.wikipedia.org/wiki/