Основные вероятностные характеристики простейшего потока

Получим некоторые, наиболее используемые, вероятностные характеристики:

– вероятность того, что в течение времени t не произойдет ни одного события, равна .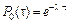

– вероятность того, что за промежуток времени tв потоке наступит хотя бы одно событие, равна .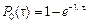

Математическое ожидание числа событий, наступивших за время t

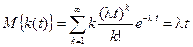
Дисперсия числа событий, наступивших за время t

.

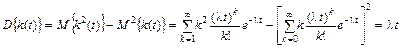Рассмотрим случайную величину, характеризующую длину интервала между моментами наступления событий простейшего потока.

Пусть t=t_k–t_k–1 есть длина интервала между двумя произвольными соседними моментами наступления событий.

По определению функция распределения F(t)=P(t<t). Эта вероятность вычисляется с помощью вероятности противоположного события, то есть

, .

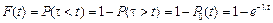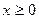Плотность распределения промежутка времени между двумя последовательными событиями получим, продифференцировав F(t) по времени.

, .

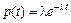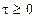Пользуясь полученной функцией плотности распределения, можно получить числовые характеристики случайной величины t: математическое ожидание M(t), дисперсию D(t) и среднеквадратическое отклонение s(t)

, , .

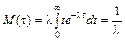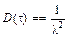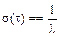Для малых Dt можно получить приближенную формулу, получаемую заменой функции e^–lDt, только двумя членами разложения в ряд по степеням Dt, тогда вероятность попадания на малый промежуток времени Dt хотя бы одного события составляет:

.

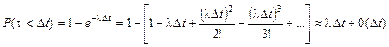Отсюда можно сделать следующий вывод: средний интервал времени t между любыми двумя соседними событиями в простейшем потоке в среднем равен 1/l и его среднеквадратическое отклонение также равно 1/l, где l – интенсивность потока, т.е. среднее число событий, происходящих в единицу времени. Закон распределения случайной величины, обладающей такими свойствами, называется показательным (или экспоненциальным), а величина l является параметром этого показательного закона. Таким образом, для простейшего потока математическое ожидание интервала времени между соседними событиями равно его среднеквадратическому отклонению.

Пример. Пусть клиенты, которые хотят получить консультацию, образуют простейший поток с параметром 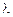. Клиентов обслуживает один работник социальной сферы, если он занят, образуется очередь. Считается, что длина очереди не ограничена. Время обслуживания одного клиента является экспоненциально распределенной случайной величиной с параметром 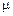. Пусть 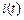– число клиентов, находящихся в системе в момент 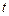. Найти финальные вероятности числа клиентов в системе.

Пусть 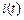есть число клиентов, находящихся в системе в момент времени 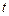. Граф вероятностей переходов для процесса 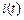изображен на рис.6.

рис.6.

Прямая система дифференциальных уравнений Колмогорова имеет вид:

,

, .

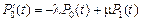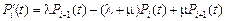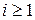Очевидно, что система уравнений для финальных вероятностей примет вид

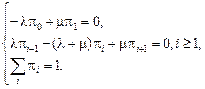
Из первого уравнения получаем .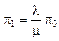

Из уравнения для : ,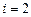

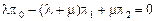получаем .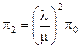

Аналогично, .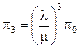

Можно показать, что .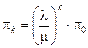

Тогда из условия нормировки получаем, что .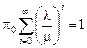

Так как ряд сходится при 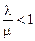, то и стационарный режим существует лишь при 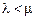. В этом случае 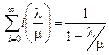, следовательно, .

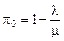Окончательно, финальные вероятности числа клиентов в системе определяются по формуле .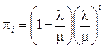

Рассмотрим пример на применение производящих функций при решении систем дифференциальных уравнений Колмогорова.

Пример. Поток клиентов, пришедших открыть счет (депозит) в банке, является простейшим с параметром 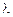, будем считать, что случайная величина, характеризующая продолжительность обслуживания счета, является экспоненциально распределенной с параметром 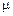. Найти распределение вероятностей числа счетов в банке в момент времени 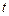, если в начальный момент времени в банке не было ни одного счета.

Пусть 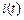есть число клиентов, счета которых обслуживаются в банке, в момент времени 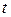. Граф вероятностей переходов для процесса 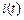изображен на рис.7

рис.7

Составляем прямую систему дифференциальных уравнений Колмогорова для распределения вероятностей :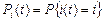

.

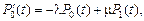
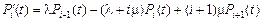Очевидно, начальные условия имеют вид:

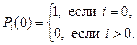
Чтобы решить систему дифференциальных уравнений, определим производящую функцию .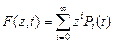

Домножим каждое уравнение системы на 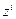и просуммируем: .

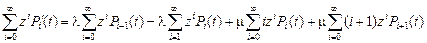При этом учитываем, что , .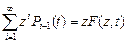

,

.

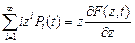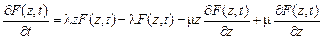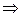
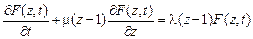Полученное уравнение является дифференциальным уравнением в частных производных первого порядка, система обыкновенных дифференциальных уравнений для характеристик которого имеет вид:

.

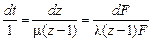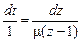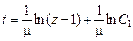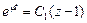Рассмотрим первое равенство . Решение этого уравнения имеет вид: , или . Отсюда .

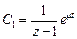Из второго равенства получим: 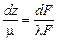, откуда следует 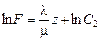. Тогда 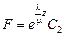, где .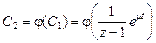

Следовательно, общее решение уравнения имеет вид: 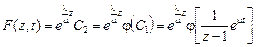, где 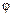– произвольная дифференцируемая функция.

Найдем ее вид, используя начальное условие :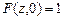

.

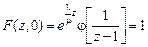Отсюда 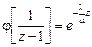. Выполнив замену 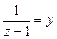, получим 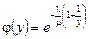. Следовательно, .

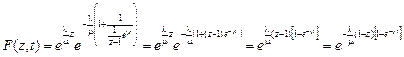Разлагая эту функцию в ряд по степеням 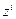, найдем вероятности 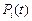следующим образом:

.

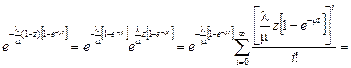
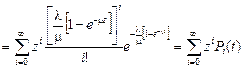Следовательно, распределение является пуассоновским с параметром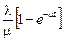

.

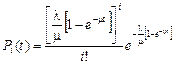Отсюда можно определить финальное распределение

.

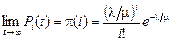Распределение 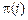является пуассоновским с параметром .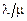