Информация в непрерывных сообщениях при наличии шумов

Рассмотрим модель источника непрерывных сообщений, представленную на рис. 1.4,

где: 1 — источник непрерывных зашумленных сообщений;

2 — идеальный источник непрерывных сообщений;

3 — сумматор.

Выходное сообщение такого устройства (у) представляет собой смесь идеального непрерывного сообщения (х) и шума (n). Будем рассматривать частный случай, когда шумы и помехи носят аддитивный характер, то есть когда выходное сообщение (у) есть сумма идеального сообщения (х) и шума (n) т.е. y = x + n

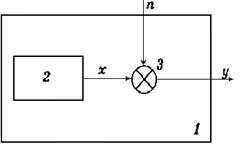
Рис. 1.4 Модель источника непрерывных сообщений.

Для определения качества информации, содержащегося в каком-либо конкретном символе непрерывного сообщения (I), можно воспользоваться основным соотношением теории информации (1.3):

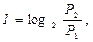(1.18)

где 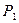— априорная вероятность появления символа сообщения;

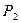— апостериорная вероятность появления того же символа сообщения.

В случае непрерывного сообщения х(t)под априорной вероятностью 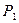следует подразумевать вероятность того, что символ сообщения х(t) заключен в интервале значений между х и 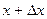. Если известна функция плотности распределения вероятности символов исходного сообщения (р(х)), то априорная вероятность 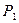имеет вид:

,

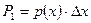а апостериорную вероятность сообщения 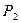можно представить в виде:

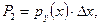
где 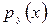— условная плотность распределения вероятностей символов сообщения х(t), когда известен конкретный символ у.

Следует отметить, что условная плотность распределения 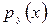представляет собой не что иное, как плотность распределения вероятностей шума 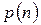. Действительно, если на выходе зашумлённого источника непрерывных сообщений зафиксирован какой-либо определённый символ y₀, то в сообщении х(t) ему соответствует символ x = y₀ – n, который имеет плотность распределения тождественную плотности распределения шума n.

Подставляя в формулу (1.18) значения вероятносте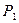й и 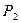и переходя к пределу при 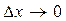, получим следующие соотношения:

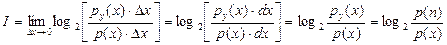(1.19)

Предельный переход в этой формуле необходим, т.к. непрерывные сообщения обладают бесконечным алфавитом.

Определяемое формулой(1.19) количество информации (I)соответствует только одной паре возможных значений непрерывного сообщения х и шума n. Так как и сообщение и помеха могут принимать бесконечное число различных, не связанных между собой, значений, то для оценки среднего количества информации, получаемой при приеме сообщения на фоне аддитивного шума, необходимо усреднить выражение (1.19) по всем возможным значениям х и n.

Для этого используются известные соотношения теории вероятностей. Так, совместная плотность распределения вероятностей событий x и y (p(x,y)) представляется в виде:

p(x,y)=p_y(x)∙p(y)= p_x(y)∙p(x),(1.20)

где p_x(y) - плотность распределения вероятности символов в сообщении y=x+n, когда переданное сообщение есть x ;

p_y(x) - условная плотность распределения вероятности символов в сообщении x , когда принятое сообщение есть y.

Известны так же следующие соотношения:

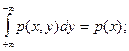
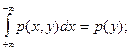(1.21)

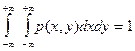
Кроме того, из (1.20) следует

.

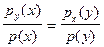Подставляя это отношение в формулу (1.19) получаем:

,

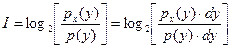С учетом того, что p_x(y)∙dy = P_x(y) есть условная вероятность появления сообщения y в интервале 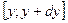, когда передаваемое сообщение есть x, а p(y)∙dy = P(y) - вероятность того, что сообщение y содержится в интервале 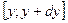при неизвестном x, предыдущее выражение преобразуется к виду

(1.22)

Это соотношение определяет количество информации, получаемой при передаче символа сообщения x, когда при приеме наблюдателю известен символ в виде суммы y = x + n.

Заметим, что p_x(y)∙по существу есть не что иное, как плотность распределения вероятностей шума n. Действительно, если задан конкретный символ сообщения x₀, то сумма y=x₀+n распределена по закону распределения шума n, который наложен на символ сообщения x₀, а следовательно,

p_x(y)∙= p(n). (1.23)

Учитывая (1.23), выражение(1.22) примет вид:

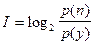. (1.24)

Для оценки среднего количества информации при приеме сообщения на фоне шума ( 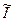) необходимо путем интегрирования по всем значениям x и y усреднить количество информации (I), приходящееся на каждое распределение вероятностей p(x,y).

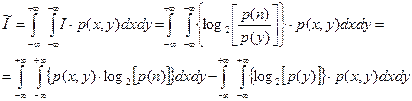. (1.25)

Очевидно, что плотность распределения вероятностей шума (n) не зависит от x и y по отдельности, а определяется только их разностью, т.к. n= y - x. Кроме того, учитывая (1.23), соотношение (1.20) можно преобразовать к виду

P(x,y)= p_x(y)∙p(y)=p(n)∙p(x), (56)

тогда первое слагаемое в (1.25) можно записать в следующем виде:

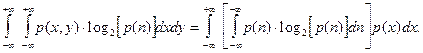
Во внутреннем интеграле dy заменено на dn , т.к. y=x + n, а при интегрировании по y величина x рассматривается как постоянная.

В такой записи внутренний интеграл, в соответствии с (1.16), представляет собой взятую со знаком минус энтропию шума (H(n)).

При стационарном шуме энтропия шума является величиной постоянной и может быть вынесена за знак интеграла, тогда первое слагаемое в выражении (1.25) преобразуется к виду:

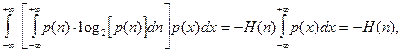
т.к.

.

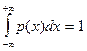Используя известное равенство (1.21), второе слагаемое выражения (1.25) легко привести к виду:

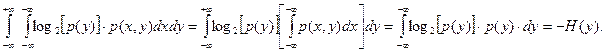(59)

Окончательно получаем:

.

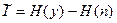Таким образом, среднее количество информации в символе непрерывного сообщения x, которую можно извлечь из зашумлённого символа y (y= x+ n) равно разности энтропий принятого сообщения y и шума n.