Заряженная сфера
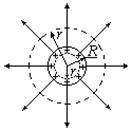 |
Пусть q — заряд, равномерно распределенный на сфере радиуса R. Очевидно, из соображений симметрии направление вектора 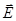 в любой точке проходит через центр сферы, а модуль вектора
в любой точке проходит через центр сферы, а модуль вектора 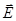 должен зависеть только от расстояния r до центра сферы. Такое поле является центрально-симметричным, силовые линии идут радиально от поверхности сферы. В качестве замкнутой поверхности надо взять концентрическую сферу. Пусть ее радиус
должен зависеть только от расстояния r до центра сферы. Такое поле является центрально-симметричным, силовые линии идут радиально от поверхности сферы. В качестве замкнутой поверхности надо взять концентрическую сферу. Пусть ее радиус 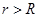 , тогда по теореме Гаусса
, тогда по теореме Гаусса 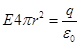 , откуда
, откуда
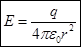 .
.
Вне заряженной поверхности поле убывает с расстоянием r по такому же закону, как у точечного заряда.
Если 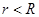 , то замкнутая поверхность не содержит внутри зарядов, поэтому в этой области всюду
, то замкнутая поверхность не содержит внутри зарядов, поэтому в этой области всюду 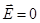 , т. е. внутри равномерно заряженной сферической поверхности электрическое поле отсутствует.
, т. е. внутри равномерно заряженной сферической поверхности электрическое поле отсутствует.
