Низкочастотные фильтры

ФНЧ, собранные по П- или Т- схеме представлены на рис.3.10.

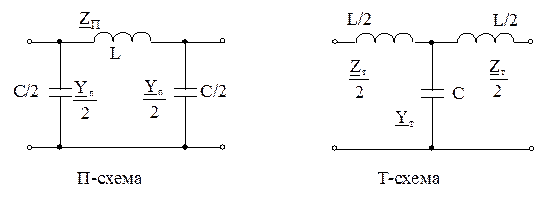
Рис. 3.10. Схемы фильтров низких частот

Из теории четырехполюсников записанных в А- форме записи

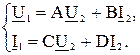(3.26)

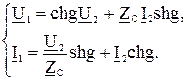(3.27)

Из сравнения (3.26) и (3.27)

A=chg=ch(a+jb). (3.28)

Для П- и Т- схем:

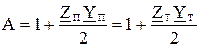, (3.29)

где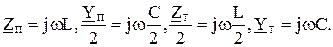

В соответствии с этим для П- и Т- схем:

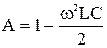. (3.30)

Из (3.30) видно, что А – положительное или отрицательное действительное число.

Из (3.28)

A=ch(a+jb)=chacosb+jshasinb. (3.31)

Уравнение (3.31) распадается на два уравнения:

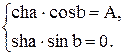(3.32)

Определим границы области пропускания. При а=0, cha=1, тогда

+1³А=cos b³ -1, (3.33)

или

, (3.34)

следовательно фильтр пропускает без затухания частоты от w=0 до граничной частоты

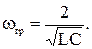(3.35)

Найдём изменение коэффициентов фазы ”b” в области пропускания фильтра.

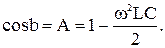
Введём 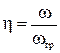, тогда

cos b=1-2h². (3.36)

Для области затухания h=1¸¥

Из (3.32) sha×sin b=0 – так как в области затухания а¹0, то

sin b=0; b=p (рис.3.11).

Для области затухания из первого равенства (3.32):

cha = -A=2h²-1. (3.37)

Из (3.37) подставляя h от 1 до ¥ определяем cha, а затем “a” (рис.3.11).

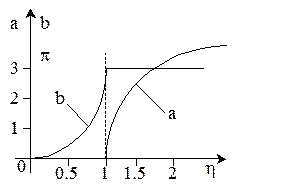
Рис.3.11. График коэффициентов затухания и фазы для ФНЧ

Рассмотрим поведение характеристического сопротивления Z_c для ФНЧ, собранных по Т и П - схеме.

Для симметричного четырёхполюсника ,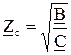

для Т-схемы - , ,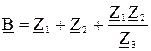

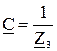для П-схемы - , .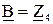

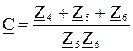Подставляя выражения для коэффициентов В и С в уравнение характеристического сопротивления и вводя относительную частоту h, получим уравнения характеристического сопротивления для ФНЧ, собранного по П-схеме- Z_сп и Т-схеме - Z_ст.

, (3.38)

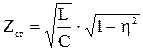. (3.39)

В уравнениях (3.38), (3.39) при большой h единицей можно пренебречь (область затухания) и тогда

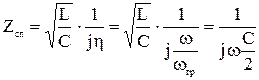-имеет емкостной характер (рис.3.12)

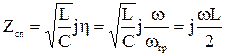-имеет индуктивный характер (рис.3.12)

В области пропускания 0 £ h £ 1 поэтому Z_ст и Z_сп носят чисто активный характер (рис.3.12).

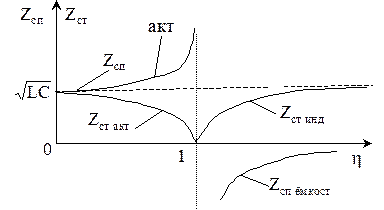
Рис. 3.12. Графики изменения характеристического сопротивления ФНЧ, собранных по Т и П –схеме

Применение той или иной схемы ФНЧ определяется условиями его работы и предъявляемыми к нему требованиями.