Электромагнитное поле в диэлектрике

Нагрев диэлектрика, помещённого в переменное электрическое поле между электродами конденсатора, происходит за счет процессов поляризации и протекание токов сквозной проводимости. Эти процессы обусловлены движением электрических зарядов в веществе под действием сил электрического поля.

Свободные заряды, т. е. заряды, которые могут перемещаться сквозь объем тела, переходя от электрода к электроду, или хотя бы перемещаются на микроскопические расстояния создают ток проводимости. Наличие структурных зарядов в структуре диэлектрика характеризуется электрической проводимостью. В зависимости от величины g различают диэлектрические материалы (g <10^-8 См/м) проводники (g <10^-8 См/м) и полупроводники.

Если электрические материалы могут смещаться только на микроскопические расстояния, то они называются связанными и их движение приводит к поляризации вещества. Каждый элемент структуры вещества: атом, молекула или элементарная ячейка кристаллической решётки состоит из связанных электрических зарядов разного знака. Такая микросистема заряда в целом электрически нейтральная, т. е. алгебраическая сумма положительных и отрицательных зарядов, входящих в микросистему, равна нулю.

Связанные заряды в микросистемах вещества - это в конечном итоге заряды элементарных частиц – протонов и электронов, входящих в состав атомов вещества. Структура атомов и взаимодействие элементов этой структуры с внешним электромагнитным полем подчиняются сложным законам квантовой механики и электродинамики, но в рамках классической теории поля Максвелла Лоренца можно использовать приближённые модели микросистем вещества. Одна из возможных моделей представляет собой совокупность связанных точечных зарядов q_{св.микро} разного знака, локализованных в микрообъёме вещества. Положительные заряды находятся в ядрах атомов, а отрицательные – в геометрических центрах электронных оболочек. Наряду с такой дискретной моделью микросистем вещества используется и непрерывная модель, где допускается существование объёмной плотности связанных зарядов r_{св.микро} как функции координат в пределах микрообъёма вещества V_микро.

Характеристикой электрических свойств системы зарядов служит электрический момент р. Для дискретной системы зарядов

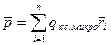(1)

для непрерывной системы

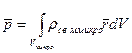(2)

где r - расстояние от заданного заряда или элемента объёма до полюса системы (см. рис. 1).

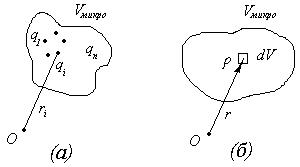
Рис.1 Дискретная (а) и непрерывная (б) система связанных зарядов

Суммирование в формуле (1) производится по всем зарядам микросистемы.

Электрический момент нейтральной системы зарядов однозначно характеризует её свойства, т. е. не зависит от выбора полюса, если только система нейтральна, то

или

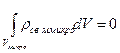(3)

Т. к. суммарные отрицательный и положительный заряды нейтральной системы равны по абсолютной величине, то такая система при р¹0 подобна диполю, т. е. совокупности равных положительного и отрицательного точечных зарядов q, разнесенных на некоторое расстояние. Если полюс системы совместить с местом нахождения отрицательного заряда, то по формуле (1) дипольный момент 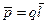, где l - плечо диполя, и векторы 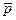и 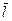направлены от отрицательного заряда к положительному.

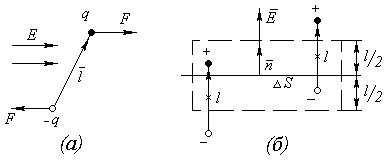
Рис. 2 Диполь в электрическом поле (а) и образование связанных зарядов на элементе поверхности (б).

Применение микроскопических характеристик поля в диэлектрике для количественного исследования процесса поляризации практически невозможно, т. к. величины r_{св.микро} и 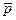недоступны непосредственному измерению. Практически используя макроскопические характеристики поля в диэлектрике, которые получается из соответствующих микроскопических величин путём усреднения поля физически бесконечно малому объёму ΔV. Этот объём в отличие от бесконечно малого математического объёма должен быть чрезвычайно велик по сравнению с расстоянием между молекулами вещества. Одновременно ΔV должен быть мал по сравнению с макроскопическими неоднородностями среды и поля. Это обеспечивает плавное изменение всех усреднённых величин при переходе в смежные элементы объёма.

Если дипольные моменты всех микросистем вещества, находящихся в объёме ΔV , геометрически сложить и вычислить предел

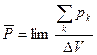(4)

то получится вектор поляризации 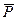. Его физический смысл – он является электрическим моментом молекул диэлектрика в единице объёма.

Скалярная величина плотности связанных зарядов усредняется по формуле

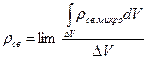(5)

здесь ΔV стремится к 0, сохраняя свой макроскопический характер.

При отсутствии внешнего электрического поля 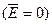- ориентация дипольных моментов микросистем диэлектрика имеет хаотический характер и вектор поляризации равен нулю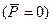

Ели в диэлектрике существует электрическое поле напряжённостью Е, то на каждый заряд диполя действует сила 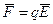, стремящееся развернуть диполь по направлению поля (рис. 2,а). Преимущественная ориентация диполей в одну сторону приводит к тому, что их геометрическая сумма в единице объёма отлична от нуля и в соответствии с формулой (4) вектор поляризации .

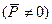Поместим внутрь диэлектрика участок поверхности ΔS и ориентируем его перпендикулярно направлению электрического поля (рис. 2). Около этого участка выделим малый цилиндрический объём, высота которого равна плечу диполя l . В таком случае все диполи числом N, попавшие внутрь цилиндрического объёма, окажутся «перерезанными» поверхностью ΔS так, что их положительные и отрицательные заряды окажутся по разные стороны поверхности. На внутренней стороне поверхности ΔS, считая по направлению нормали, окажется отрицательный связанный заряд, поверхностная плотность которого

Вектор поляризации в рассматриваемом объеме имеет только одну нормальную

составляющую Р_n. В соответствии с формулой (4) находим

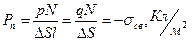(6)

т. к. модуль дипольного момента p=ql.

Дополняя участок поверхности ΔS до замкнутой поверхности S, лежащей целиком внутри диэлектрика, и используя равенство (6), вычислим поток вектора поляризации

где Q_св - суммарный связанный заряд в объёме V, ограниченном поверхностью S.