Дисперсия. Среднее квадратическое отклонение
Пусть имеется случайная величина 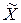 с математическим ожиданием M[X]. Отклонение случайной величины
с математическим ожиданием M[X]. Отклонение случайной величины 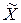 от ее математического ожидания,называется центрированной случайной величиной
от ее математического ожидания,называется центрированной случайной величиной 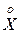 , соответствующей величине
, соответствующей величине 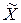 :
:
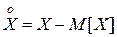 (I.6)
(I.6)
Таким образом, математическое ожидание центрированной случайной величины равно нулю.
Дисперсиейслучайной величины 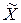 называется математическое ожидание квадрата соответствующей центрированной случайной величины.
называется математическое ожидание квадрата соответствующей центрированной случайной величины.
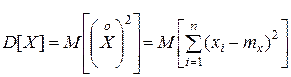 (I.7)
(I.7)
Дисперсия вычисляется по следующим формулам:
· для дискретной случайной величины
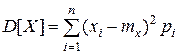 (I.8)
(I.8)
· для непрерывной случайной величины
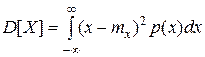 . (I.8)
. (I.8)
Дисперсия случайной величины является характеристикой рассеивания значений случайной величины около ее математического ожидания. Она имеет размерность квадрата случайной величины. В практических расчетах для оценки рассеивания удобнее пользоваться величиной, размерность которой совпадает с размерностью самой случайной величины. Такую величину называют средним квадратическим отклонением (иначе – «стандартом») случайной величины 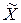 :
:
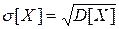 (I.9)
(I.9)
Для упрощения записи можно пользоваться сокращенными обозначениями для математического ожидания, дисперсии и среднего квадратического отклонения соответственно: mx , Dx, 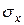 .
.
