Динамические и статистические закономерности

Молекулярная физика или молекулярно-кинетическая теория является статистической теорией, т. е. теорией, которая рассматривает поведение систем, состоящих из огромного числа частиц (атомов, молекул), на основе вероятностных моделей. Она стремится на основе статистического подхода установить связь между экспериментально измеренными макроскопическими величинами (давление, объем, температура и т.д.) и микроскопическими характеристиками частиц, входящих в состав системы (масса, импульс, энергия и т.д.).

В отличие от молекулярно-кинетической теории, термодинамика при изучении свойств макроскопических систем не опирается ни на какие представления о молекулярной структуре вещества. Термодинамика является наукой феноменологической. Она делает выводы о свойствах вещества на основе законов, установленных на опыте, таких, как закон сохранения энергии. Термодинамика оперирует только с макроскопическими величинами (давление, температура, объем и т.п.), которые вводятся на основе физического эксперимента.

Оба подхода – термодинамический и статистический – не противоречат, а дополняют друг друга. Только совместное использование термодинамики и молекулярно-кинетической теории может дать наиболее полное представление о свойствах систем, состоящих из большого числа частиц.

Основное уравнение кинетической теории газов.

, где k является постоянной Больцмана (отношение универсальной газовой постоянной R к числу Авогадро N_A), i — число степеней свободы молекул (i = 3 в большинстве задач про идеальные газы, где молекулы предполагаются сферами малого радиуса, физическим аналогом которых могут служить инертные газы), а T - абсолютная температура.

Основное уравнение МКТ связывает макроскопические параметры (давление, объём, температура) газовой системы с микроскопическими (масса молекул, средняя скорость их движения).

Уравнение Клайперона-Менделеева

уравнение состояния идеального газа (его также называют уравнением Клапейрона-Менделеева):

PV = nRT где n – число молей газа;P – давление газа (например, в атм;V – объем газа (в литрах);T – температура газа (в кельвинах);R – газовая постоянная (0,0821 л·атм/моль·K).

Закон Бойля-Мариотта

Закон является частным случаем уравнения состояния идеального газа.

Закон Бойля — Мариотта гласит:

При постоянной температуре и массе идеального газа произведение его давления и объёма постоянно.

В математической форме это утверждение записывается следующим образом

pV = const,где p — давление газа; V — объём газа.

Важно уточнить, что в данном законе газ рассматривается, как идеальный. На самом деле, все газы в той или иной мере отличаются от идеального. Чем выше молярная масса газа, тем больше это отличие.

Закон Гей-Люссака

Изобарический закон, открытый Гей-Люссаком в 1802 году утверждает, что при постоянном давлении объём постоянной массы газа пропорционален абсолютной температуре. Математически закон выражается следующим образом:

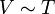или где V — объём газа, T — температура.

Если известно состояние газа при неизменном давлении и двух разных температурах, закон может быть записан в следующей форме:

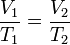или .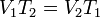

Закон Шарля

Формулировка закона Шарля следующая:

Давление газа фиксированной массы и фиксированного объёма прямо пропорционально абсолютной температуре газа.

Проще говоря, если температура газа увеличивается, то и его давление тоже увеличивается, если при этом масса и объём газа остаются неизменными.Закон имеет особенно простой математический вид, если температура измеряется по абсолютной шкале, например, в градусах Кельвина. Математически закон записывают так:

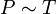Или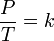 гдеP — давление газа,

T — температура газа (в градусах Кельвина),

k — константа.

Этот закон справедлив, поскольку температура является мерой средней кинетической энергии вещества. Если кинетическая энергия газа увеличивается, его частицы сталкиваются со стенками сосуда быстрее, тем самым создавая более высокое давление.

Для сравнения того же вещества при двух различных условиях, закон можно записать в виде:

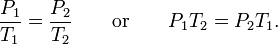
Закон Дальтона

или закон парциальных давлений. Он основан на том, что в смеси газов каждый газ оказывает такое же давление, какое он оказывал бы, если бы в сосуде присутствовал один.

Давление компонентов газовой смеси зависит только от числа молей каждого из них, так как температура и объем для всех газов в смеси одинаковы.

Давление каждого из газов называют парциальным давлением. Согласно закону парциальных давлений Дальтона, общее давление газовой смеси равно сумме парциальных давлений:

Pобщ= P1+ P2+ P3+ ... + PN. (1.20)

Если V – общий объем, а n1, n2, n3и т.д. – число молей каждого компонента, то

PV=n1RT+n2RT+n3RT+...+nNRT=RT(n1+n2+n3+...+nN). (1.21)

Парциальное давление одного из газов, допустим 1, будет равно

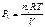. (1.22)

Понятно, что отношение парциального давления газа к его общему давлению равно отношению числа молей этого компонента к числу молей всех газов в смеси:

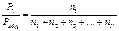. (1.23)

Это отношение называют молярной долей и обозначают символом Х. Для газа 1 молярная доля равна Х1и т.д. Парциальное давление учитывается во многих расчетах. Например, операции по измерению объемов, включающих сбор газов над поверхностью воды, требуют учета парциального давления паров воды в газовой смеси. По сравнению с водяными парами пары ртути имеют значительно более низкое давление, и это создает ощутимые преимущества при использовании ртути в качестве вытесняемой жидкости, так как парциальным давлением паров ртути в таких расчетах вполне можно пренебречь.

С другой стороны, хорошо известно, что вдыхаемый нами воздух является смесью газов. Выдыхаемый воздух отражает происходящий в легких процесс газового обмена. Он насыщен парами воды. Парциальное давление водяного пара достаточно заметно и равно приблизительно 48 мм.р.с. Поэтому, если общее давление выдыхаемого воздуха равно 760 мм, то давление, обусловленное смесью газов О₂ + СО₂ + N₂, будет равно не 760, а 760 – 48 = 712 мм.р.с.

Закон Авогадро