Определение 6

Прямая называется асимптотой графика функции у = f (х) (кривой f (х)), если расстояние δ от переменной точки М кривой до этой прямой при удалении точки М в бесконечность стремится к нулю.

Различают асимптоты вертикальные (т.е. параллельные оси ординат) и наклонные (т.е. не параллельные оси ординат).

1. Вертикальные асимптоты.

Если асимптота параллельна оси ординат, то она имеет уравнение х = а и называется вертикальной асимптотой. Из определения следует, что прямая х= а - асимптота кривой f (х) в том и только том случае, когда хотя бы один из пределов 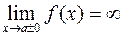. Таким образом, а - точка бесконечного разрыва функции f (x).

Следовательно, для отыскания вертикальных асимптот нужно найти такие значения х=а, при приближении к которым функция y = f (x) стремится к бесконечности. Тогда прямая х=а будет вертикальной асимптотой.

2. Наклонные асимптоты.

Пусть кривая y=f (x) имеет асимптоту не параллельную оси ординат, уравнение которой запишем в виде

y = kx + b

Для нахождения чисел k и b воспользуемся следующими соотношениями

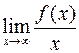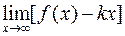k = , b = (1)

Итак, если прямая y = kx + b есть асимптота кривой f (x) , то k и b находятся как выше приведенные пределы. Обратно, если существуют рассмотренные пределы, то прямая y = kx + b есть асимптота функции f (x). Если не существует хотя бы один из пределов, то кривая наклонной асимптоты не имеет. При этом указанные пределы могут быть различными при х ® + ¥ ( для правой наклонной асимптоты) и при х ® - ¥ (для левой наклонной асимптоты). При вычислении пределов удобно использовать правило Лопиталя.

Частный случай наклонной асимптоты у = b (при k = 0) носит название горизонтальной асимптоты. Для координат точки М (х,f (х)) имеем: в случае вертикальной асимптоты х ® а, у = f (х) ® ¥, в случае горизонтальной асимптоты х ® ¥, у = f (х) ® b и в случае произвольной наклонной асимптоты х ® ¥, у = f (х) ® ¥.