Метод решения транспортной задачи
Задача (3.1.1), (3.1.6), (3.1.7), (3.1.4) является задачей ЛП. В силу условия (3.1.5) одно из уравнений (3.1.6), (3.1.7) оказывается зависимым, т.е. транспортная модель содержит 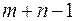 независимых уравнений. Поэтому начальное БДР должно иметь
независимых уравнений. Поэтому начальное БДР должно иметь 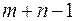 базисных переменных. Опишем основные шаги алгоритма решения ТЗ.
базисных переменных. Опишем основные шаги алгоритма решения ТЗ.
1) Найти начальное БДР.
2) Найти из числа небазисных переменных вводимую в базис. Если все небазисные переменные удовлетворяют условию оптимальности (симплекс-метода), закончить вычисления; иначе перейти на п.3.
3)Выбрать выводимую из базиса переменную (используя условие допустимости) из числа переменных текущего базиса. Затем найти новое базисное решение. Перейти на п.2.
Исходные данные ТЗ записывают в виде таблицы:
| Пункты | пункты назначения | производство | ||||
| Отправления | 1 | j | n | |||
| 1 |  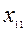 | 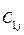 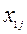 | 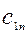 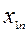 | 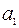 | ||
| i | 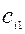 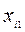 | 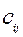 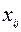 | 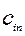 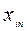 | 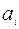 | ||
| m | 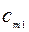 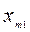 | 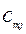 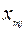 | 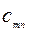 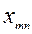 | 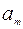 | ||
| Потребление | 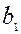 | 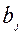 | 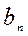 |
Метод решения ТЗ рассмотрим на примере. В таблицу внесем данные ТЗ: 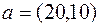 ,
, 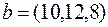 ,
, 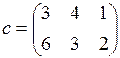 .
.
| пункты | Пункты назначения |  | ||
| Отправления |  |  | 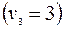 | |
 | 4 -  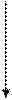 10 10 |  1 + 1 + | ||
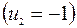 | 3 +  2 2 | 2 - | ||
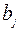 |
Определение БДР.Начальное БДР можно найти, например, по правилу северо-западного угла.
1. Определить перевозку для левого верхнего угла, определяемую величиной исчерпания либо пункта потребления, либо пункта производства.
2. В зависимости от исчерпания пункта производства ( потребления ) удалить строку ( столбец ) из таблицы, задав ненулевыми объемы перевозок удаляемых клеток. В случае исчерпания как пункта потребления, так и пункта производства удаляется произвольно либо строка, либо столбец, а на следующем шаге будет получена нулевая базисная переменная.
3. Повторить действия для оставшейся части таблицы.
В таблицу вносятся значения объемов перевозок только для базисных переменных.
Вычисление критерия оптимальности.В ТЗ вычисление критерия оптимальности (2.8.1) осуществляется по схеме (2.8.2), а коэффициенты p вычисляются посредством решения системы (2.8.3).
Обозначим 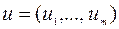 ,
, 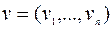 , коэффициенты
, коэффициенты 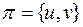 соответственно для уравнений (3.1.7), (3.1.6). Поскольку одно из уравнений (3.1.6), (3.1.7) лишнее, произвольно полагают одно из значений
соответственно для уравнений (3.1.7), (3.1.6). Поскольку одно из уравнений (3.1.6), (3.1.7) лишнее, произвольно полагают одно из значений 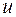 либо
либо 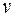 заданным, например,
заданным, например, 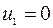 . Уравнения (2.8.3) для базисных переменных приобретают вид
. Уравнения (2.8.3) для базисных переменных приобретают вид
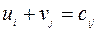 . (3.2.1)
. (3.2.1)
Условие оптимальности (2.4.7) в форме (2.8.2), с учетом представления вектора 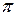 записываются в виде
записываются в виде
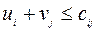 (3.2.2)
(3.2.2)
Для ввода в базис выбирается переменная xij с наибольшим положительным значением величины 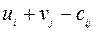 . Решение получено, если выполняются неравенства (3.2.2).
. Решение получено, если выполняются неравенства (3.2.2).
Для таблицы запишем уравнения (3.2.1) и их решение, полагая 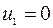 .
.
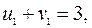
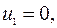
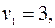
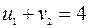 ,
, 
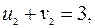
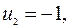
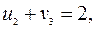
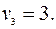
Вычислим значения критерия для небазисных переменных
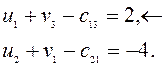
Отсюда следует, что переменную x13 следует вводить в базис.
Выбор переменной, выводимой из базиса.В симплекс-методе при вводе переменной в базис изменяются только базисные переменные, одна, или несколько из которых обращаются в нуль. В ТЗ строится замкнутый цикл, состоящий из горизонтальных и вертикальных линий, узлы которого находятся в клетках таблицы, соответствующих базисным переменным и переменной, вводимой в базис. Для каждого базисного решения и соответствующей небазисной переменной можно построить лишь один цикл.
Небазисная переменная цикла будет возрастать. Для сохранения объемов перевозок в соседних к ней узлах цикла клетках значения 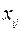 должны убывать. Клетки, в которых переменные убывают, помечаются знаком ‘-‘, в других - знаком ‘+’.
должны убывать. Клетки, в которых переменные убывают, помечаются знаком ‘-‘, в других - знаком ‘+’.
Общая величина убывания определяется минимальным значением базисных переменных, которые убывают. Обозначим эту величину 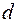 . После определения величины
. После определения величины 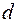 производится изменение переменных в соответствии со знаком, поставленным при обходе цикла. После этого одна из нулевых базисных переменных удаляется из базиса. Результаты сводятся в новую таблицу:
производится изменение переменных в соответствии со знаком, поставленным при обходе цикла. После этого одна из нулевых базисных переменных удаляется из базиса. Результаты сводятся в новую таблицу:
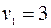 | 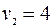 | 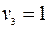 | |
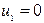 | |||
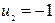 |
Процесс заканчивается, когда будут выполнены условия (3.2.2).
