Винтовые зубчатые механизмы

При помощи винтовых зубчатых механизмов легко осуществляется передача вращения между скрещивающимися осями. Известно, что аксоидами (начальными поверхностями) относительного движения в этом случае являются однополосные гиперболоиды, имеющие линейный контакт по прямой Т–Т (рис. 58).

б)

а)

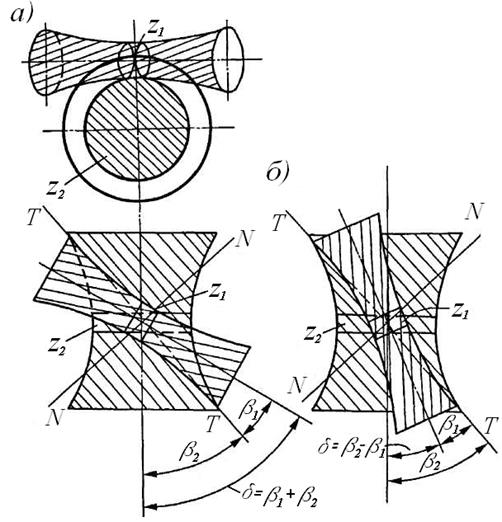
Рис. 58. Винтовой зубчатый механизм

Если на таких поверхностях нарезать зубья (z₁и z₂) с одинаковым шагом (модулем) в направлении общей нормали 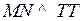, то получим гиперболоидное зацепление с постоянным передаточным отношением. Существенными недостатками такого зацепления являются большое скольжение, низкий КПД, сложность изготовления.

Из-за сложности изготовления зубьев практически используется лишь узкая горловая часть начальных гиперболоидов, которая, в свою очередь, заменяется вписанными в горловины гиперболоидов цилиндрами. В результате замены получаем касание начальных цилиндров в точке, а не по линии.

Образование таких винтовых зубьев можно представить себе следующим образом. Если в плоскости Q, касательной к основному цилиндру r_b (рис. 59, а), взять прямую АВ под некоторым углом 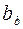и обкатывать (наматывать) плоскость вокруг неподвижного цилиндра, то все точки прямой АВ будут описывать эвольвенты в плоскостях, перпендикулярных оси цилиндра – торцевых сечениях.

а) 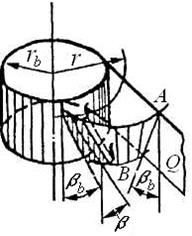б)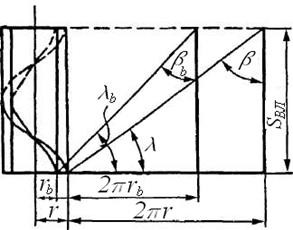

Рис. 59. Образование винтовых зубьев

В целом образуется линейчатая винтовая поверхность зуба, легко получаемая в производстве методом обкатки, подобно производству прямозубых цилиндрических колес. В любом торцевом сечении имеем обычный эвольвентный зуб с обычными геометрическими зависимостями. Начала всех эвольвент образуют на поверхности основного цилиндра винтовую линию с углом наклона 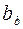. При пересечении поверхности зуба цилиндром некоторого радиуса r образуется также винтовая поверхность с углом наклона 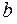. Соотношение между ходом винтовой линии и углом наклона устанавливается из принципа образования винтовой линии (рис. 59, б): . В частности,

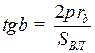. (8.1)

Отсюда

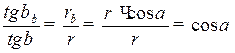. (8.2)

В сечении винтового зубчатого колеса делительным цилиндром r принято различать три шага и соответственно им – три модуля (рис. 60): нормальный 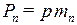; осевой 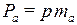; торцевой .

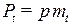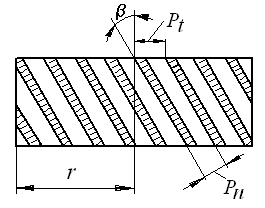
Рис. 60. К определению зависимости 9.3.

т. е.

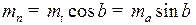. (8.3)

Условием сопряженности двух винтовых эвольвентных колес является равенство их нормальных модулей m_n, которые чаще всего являются модулями зуборезных инструментов.

Углы наклона зубьев по начальным цилиндрам могут быть любыми (следовательно, торцевые и осевые модули разными). На рис. 61, 62 показано зацепление двух винтовых зубчатых колес с углами наклона зубьев ₁ и ₂.

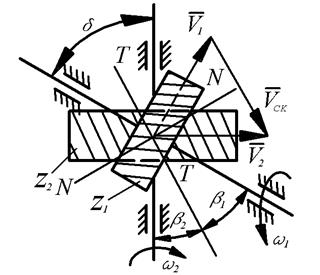
Рис. 61. Зацепление двух винтовых зубчатых колес
при одинаковом направлении наклона зубьев

Угол скрещивания осей 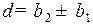. Знак «плюс» берется при одинаковом направлении наклона зубьев, а «минус» – при разном.

Обычно принимают одинаковое направление винтовой линии (рис. 61) и только при малых углах 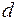возможно применение разного направления наклона зубьев (рис. 62).

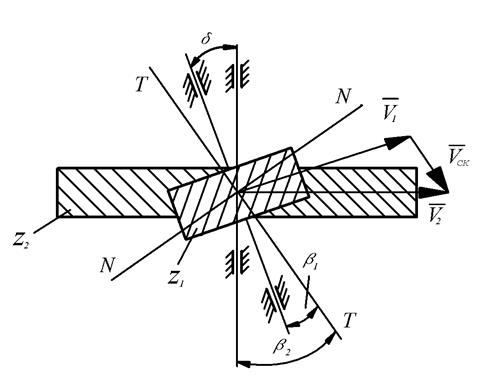
Рис. 62. Зацепление двух винтовых зубчатых колес
при разном направлении наклона зубьев

В полюсе зацепления проекции скоростей на общую нормаль NN должны быть равны, т. е.:

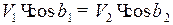или .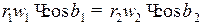

Отсюда

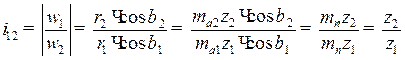. (8.4)

Последнее уравнение показывает, что даже при равных радиусах (r₁и r₂) можно получить передаточное отношение 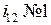за счет разных углов ₁ и ₂.

Для обеспечения коэффициента перекрытия 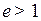принимают ширину зубчатых колес равной:

.

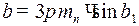Скорость скольжения:

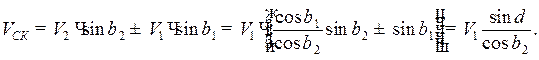(8.5)

С увеличением окружных скоростей и угла скрещивания осей скорость скольжения растет, вызывая усиленный износ поверхностей зубьев и потери на трение.

Без учета потерь на трение сила Р_н, действующая по общей нормали винтовых зубчатых колес, лежит в нормальной плоскости NN и может быть представлена в виде трех составляющих: окружной Р, радиальной Р_r и осевой Р_а (рис. 63).

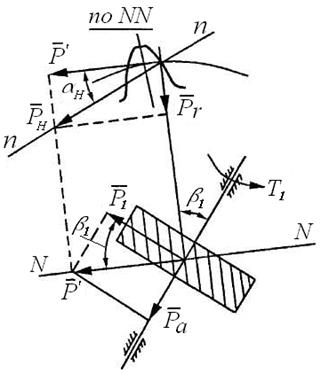
Рис. 63. К определению силы Р_H

При этом:

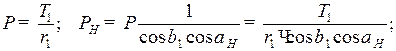
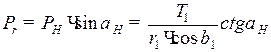; (8.6)

.

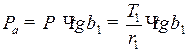Винтовые, а точнее, гиперболоидные зубчатые колеса можно рассматривать как общий случай зацепления при произвольном расположении осей в пространстве. Другие зацепления являются его частными случаями.

Если при одинаковом направлении зубьев (рис. 58, а) уменьшить угол 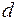до нуля, то образуется прямозубое цилиндрическое зацепление ( ).

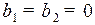Если углы наклона зубьев двух винтовых колес равны ( 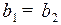), а направления винтовых линий разные, образуется винтовое зацепление при параллельных осях 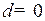(рис. 58, б), называемое обычно косозубым зубчатым зацеплением. В таком зацеплении контакт линейный, а расчет проводится для эквивалентных им прямозубых цилиндрических колес, у которых

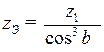. (8.7)

При большом угле наклона зубьев на одном из винтовых зубчатых колес образуется червячное зацепление.

ЧЕРВЯЧНЫЕ МЕХАНИЗМЫ

Увеличивая угол наклона 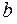(рис. 59, б), можно получить винтовую шестерню с малым числом зубьев (вплоть до одного зуба).

Если 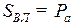(рис. 64, а), то образуется винтовое зубчатое колесо, имеющее в торцевом сечении только один зуби отличающееся от обычного болта только формой профиля.

а) 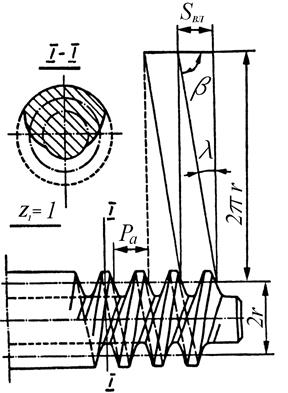б)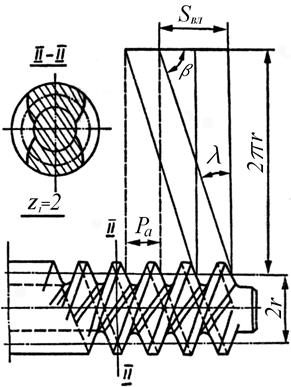

Рис. 64. Червяк:

а) однозаходный; б) двухзаходный

Если 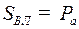(рис. 64, а), то образуется винтовое зубчатое колесо, имеющее в торцевом сечении только один зуб и отличающееся от обычного болта только формой профиля. Если S_BJl = 2Р_а (рис. 64, б), то образуется винтовое зубчатое колесо с число зубьев z₁ = 2. Очевидно, в общем виде S_BЛ = z₁P_a, т. е. число зубьев такого зубчатого колеса есть не что иное, как число заходов винтовой линии на поверхности цилиндра колеса. Такое малозубое винтовое колесо получило название червяка. Обычно число заходов червяка z_Ч = z₁ = 1 – 4.

Из условия образования винтовой линии следует:

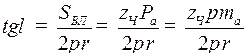, (9.1)

где 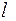– угол подъема винтовой линии червяка.

Отсюда

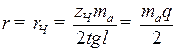, (9.2)

где – число модулей в диаметре делительной окружности червяка.

Червяк входит в зацепление с винтовым колесом в большинстве случаев при прямом угле скрещивания осей ( 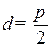), образуя червячный механизм (рис. 65).

б)

а)

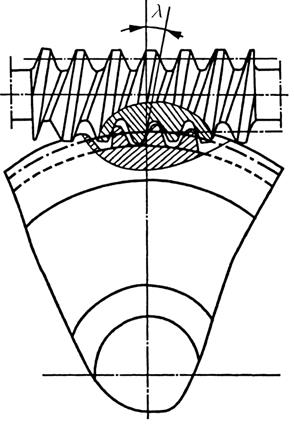
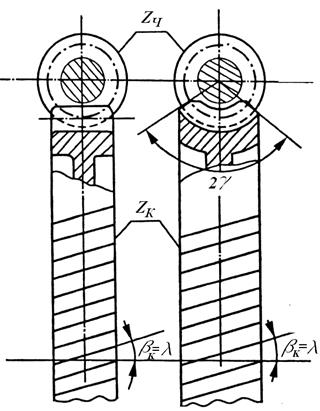
Рис. 65. Червячный механизм

Угол наклона зубьев 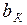на колесе при 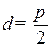равен углу подъема винтовой линии на червяке .

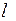Для червяка:

.

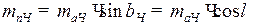Для червячного колеса:

.

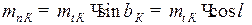Торцевой модуль червячного колеса принимается стандартным.

Передаточное отношение червячного механизма находим из выражения (9.3):

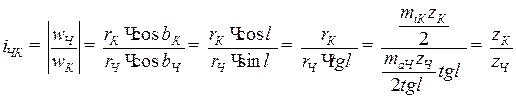. (9.3)

Чтобы избежать точечного контакта и, следовательно, повысить нагрузочную способность, червячное колесо часто выполняется с зубьями, охватывающими червяк на некотором угле 2 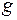= 60÷110° (рис. 65). Нарезаются такие зубья при помощи червячной фрезы, копирующей по основным размерам червяк. Поэтому величина q с целью уменьшения типоразмеров червячных фрез стандартизована (ГОСТ 9672-74).

Достоинства червячных механизмов:

- возможность осуществления большого передаточного числа в одном зацеплении (в приборных механизмах i_ЧK достигает 1000);

- компактность и малые габариты;

- плавность и бесшумность в работе;

- возможность самоторможения при 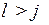, где 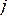– угол трения ( );

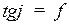- малые величины мертвого хода.

Недостатки червячных механизмов:

- большие потери на трение и, следовательно, малый коэффициент полезного действия, чтобы уменьшить потери на трение, приходится применять дорогую высококачественную бронзу для зубьев червячного колеса;

- высокие требования к точности изготовления и сборки для обеспечения контакта по линии (рис. 65);

- высокая стоимость инструмента для нарезания червячного колеса.

ВОЛНОВАЯ ПЕРЕДАЧА

Волновые зубчатые передачи (ВЗП) применяются в приводах лучших зарубежных и отечественных роботов и имеют следующие достоинства: постоянное передаточное отношение, небольшие габариты и малую массу при высокой нагрузочной способности.

Принципиальное отличие этих передач от других зубчатых передач заключается в том, что в их состав входят гибкие звенья. Благодаря деформации звеньев появляется возможность передавать движение через герметичную стенку. Это определяет области применения волновых передач, среди которых, например, электронная, химическая промышленность, космические исследования и т. п.

Кинематическая схема ВЗП изображена на рис. 66.

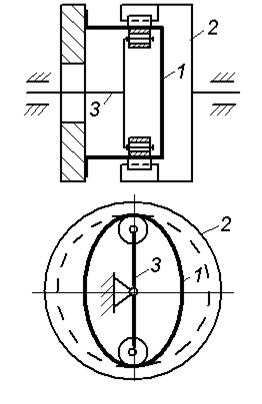
Рис. 66. Волновая зубчатая передача

Генератор колебаний 3 оснащен двумя роликами (т. е. за один оборот генерирует две волны зацеплений).

Гибкое колесо 1 представляет собой тонкостенную цилиндрическую оболочку, с одной стороны которой имеется зубчатый венец, а другая сторона герметично закреплена на неподвижной стенке. Под действием генератора волн гибкое колесо в торцевом сечении зубчатого венца становится некруглым, и в местах расположения роликов зубчатый венец гибкого колеса входит в зацепление с зубьями жесткого колеса 2. Контур деформированного колеса получает две волны деформации.

Чаще всего применяют двухволновые генераторы, у которых числа зубьев гибкого и жесткого колес связаны соотношением:

z₂ – z₁ = 2. (10.1)

При вращении двухволнового генератора каждая волна деформации перемещается по периметру гибкого колеса. В результате каждый зуб гибкого колеса за один оборот генератора волн дважды входит в зацепление с жестким колесом.

Передаточное отношение определяют следующим образом.

Если остановить гибкое колесо, то при повороте генератора волн на угол 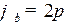жесткое колесо повернется в том же направлении, что и генератор волн, на угол :

,

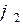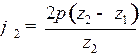где 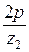– угловой шаг жесткого колеса;

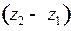– число волн деформации.

Тогда передаточное отношение от генератора волн к жесткому колесу

. (10.2)

Если остановить жесткое колесо, то за один оборот генератора волн 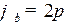вал гибкого колеса повернется в противоположном направлении на угол :

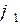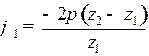, (10.3)

где 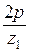– угловой шаг гибкого колеса;

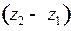– число волн деформации.

Следовательно, передаточное отношение от генератора волн к гибкому колесу

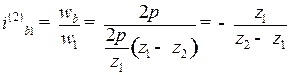. (10.4)

КУЛАЧКОВЫЕ МЕХАНИЗМЫ