Марковские сети массового обслуживания
До сих пор рассматривались марковские системы, в которых каждое требование проходило одну операцию обслуживания. Такие системы можно называть однофазными. Далее рассматриваются системы с многофазным обслуживанием, в которых требование получает обслуживание более чем о водном приборе (узле). Таким образом, можно говорить о сети узлов, каждый из которых представляет собой СМО (некоторые узлы могут иметь несколько обслуживающих приборов) с накопителем для образования очереди. Требования поступают в систему в различных точках, ждут в очередях обслуживания и, покинув один узел, поступают в другой для дальнейшего обслуживания.
При исследовании сетей возникает много новых аспектов. Например, важной становится топологическая структура сети, так как она определяет возможные переходы между узлами. Требуется также каким-нибудь способом описать пути отдельных требований. Большое значение имеет описание природы вероятностных потоков с помощью основных вероятностных процессов; например, в случае последовательной цепочки СМО, при которой требование, покидающее i-й узел, сразу поступает на обслуживание в 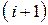 -й узел; очевидно, что промежутки времени между последовательными уходами требований из предыдущего узла равны промежуткам времени между последовательными поступлениями в следующий узел.
-й узел; очевидно, что промежутки времени между последовательными уходами требований из предыдущего узла равны промежуткам времени между последовательными поступлениями в следующий узел.
Рассмотрим простейшую последовательную систему с двумя узлами, показанную на рис. 1.
 |
Рис. 1. Система с двумя последовательными узлами
Каждый овал на этом рисунке изображает СМО, состоящую из очереди и обслуживающего прибора; внутри каждого овала указан номер узла (важно не путать такие схемы физических сетей с абстрактными диаграммами интенсивностей переходов, которые были использованы ранее). Предположим, что входящий поток является пуассоновским с интенсивностью 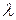 , причем каждое требование поступает сначала в узел 1; предположим также, что этот узел содержит единственный обслуживающий прибор, время обслуживания которого распределено по показательному закону с интенсивностью
, причем каждое требование поступает сначала в узел 1; предположим также, что этот узел содержит единственный обслуживающий прибор, время обслуживания которого распределено по показательному закону с интенсивностью 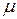 . Таким образом, узел 1 представляет собой в точности СМО типа M/M/1. Предположим, далее, что узел 2 также состоит из единственного обслуживающего прибора с показательным временем обслуживания с интенсивностью
. Таким образом, узел 1 представляет собой в точности СМО типа M/M/1. Предположим, далее, что узел 2 также состоит из единственного обслуживающего прибора с показательным временем обслуживания с интенсивностью 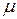 . Основная задача состоит в вычислении распределения промежутков времени между последовательными требованиями, поступающими в узел 2; это естественно, эквивалентно задаче вычисления распределения промежутков времени между последовательными требованиями, уходящими из узла 1.
. Основная задача состоит в вычислении распределения промежутков времени между последовательными требованиями, поступающими в узел 2; это естественно, эквивалентно задаче вычисления распределения промежутков времени между последовательными требованиями, уходящими из узла 1.
Пусть 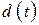 означает плотность распределения вероятностей промежутков между последовательными требованиями на выходе узла 1 и, как обычно, пусть
означает плотность распределения вероятностей промежутков между последовательными требованиями на выходе узла 1 и, как обычно, пусть 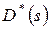 означает ее преобразование Лапласа. Перейдем к вычислению
означает ее преобразование Лапласа. Перейдем к вычислению 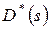 в момент, когда требование покидает узел 1. Возможно одно из двух событий: либо в очереди имеется второе требование, готовое немедленно поступить на обслуживание в узел 1, либо требования нет (накопитель пуст). В первом случае промежуток времени, через которое это следующее требование покинет узел 1, распределен точно также, как и время обслуживания
в момент, когда требование покидает узел 1. Возможно одно из двух событий: либо в очереди имеется второе требование, готовое немедленно поступить на обслуживание в узел 1, либо требования нет (накопитель пуст). В первом случае промежуток времени, через которое это следующее требование покинет узел 1, распределен точно также, как и время обслуживания 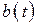 , и в этом случае получаем
, и в этом случае получаем
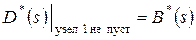 .
.
С другой стороны, если при уходе рассматриваемого первого требования узел оказывается пустым, то приходится ожидать в течение двух промежутков времени: первый промежуток – время до поступления следующего требования и второй – время обслуживания этого требования. Так как эти два промежутка распределены независимо, то плотность распределения вероятностей их суммы равна свертке плотностей распределения суммируемых величин. Соответственно преобразование Лапласа плотности распределения суммы равно произведению преобразований исходных плотностей распределения, и следовательно,
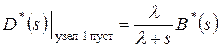 ,
,
где для преобразования Лапласа плотности распределения промежутков между поступающими требованиями уже известно явное выражение. Так как время обслуживания является показательно распределенной случайной величиной, то можно записать 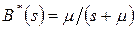 ; кроме того, как было показано ранее, вероятность того, что требование покинет систему пустой, а именно, равна
; кроме того, как было показано ранее, вероятность того, что требование покинет систему пустой, а именно, равна 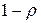 . Это позволяет записать следующее безусловное преобразование Лапласа для плотности распределения промежутков времени между уходящими требованиями:
. Это позволяет записать следующее безусловное преобразование Лапласа для плотности распределения промежутков времени между уходящими требованиями:
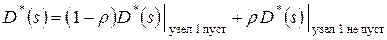 .
.
Используя проделанные ранее вычисления, получаем
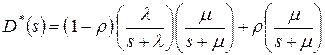 .
.
Простые алгебраические преобразования дают
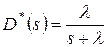 (1)
(1)
и, следовательно, распределение промежутков времени между уходящими требованиями
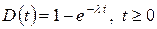 .
.
В самом деле 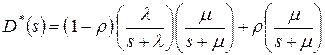 =
=
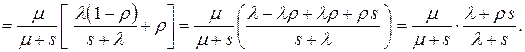
Делая подстановку 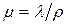 , получаем
, получаем
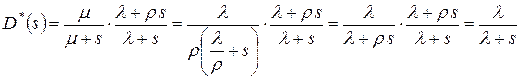 .
.
Таким образом, приходим к замечательному выводу о том, что промежутки времени между уходящими требованиями, так же как и промежутки времени между поступающими требованиями, распределены по показательному закону с тем же самым параметром. Иначе говоря (в случае стационарной СМО), входящий поток, протекая через обслуживающий прибор с показательным распределением времени обслуживания, порождает выходящий пуассоновский поток. Этот основополагающий результат обычно называют теоремой Берке.
Фактически теорема Берке говорит больше, а именно, что исходящий поток стационарной СМО типа M/M/m с пуассоновским входящим потоком с параметром 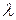 и показательным распределением времени обслуживания с параметром
и показательным распределением времени обслуживания с параметром 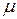 в каждом из m приборов является пуассоновским с тем же параметром
в каждом из m приборов является пуассоновским с тем же параметром 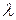 .
.
 Доказано также, что система M/M/mявляется единственной системой с обслуживанием в порядке поступления, обладающей таким свойством. Возвращаясь к рис. 1, видим, что в узел 2 поступает независимый пуассоновский поток, и, следовательно, этот узел также представляет собой систему M/M/1, что позволяет рассматривать его независимо от узла 1. Тем самым теорема Берке говорит о том, можно соединить последовательно[1] несколько узлов, состоящих из многолинейных СМО (с показательным распределением времени обслуживания для каждого прибора), и при этом будет сохраняться описанное свойство разложения на отдельные узлы.
Доказано также, что система M/M/mявляется единственной системой с обслуживанием в порядке поступления, обладающей таким свойством. Возвращаясь к рис. 1, видим, что в узел 2 поступает независимый пуассоновский поток, и, следовательно, этот узел также представляет собой систему M/M/1, что позволяет рассматривать его независимо от узла 1. Тем самым теорема Берке говорит о том, можно соединить последовательно[1] несколько узлов, состоящих из многолинейных СМО (с показательным распределением времени обслуживания для каждого прибора), и при этом будет сохраняться описанное свойство разложения на отдельные узлы.
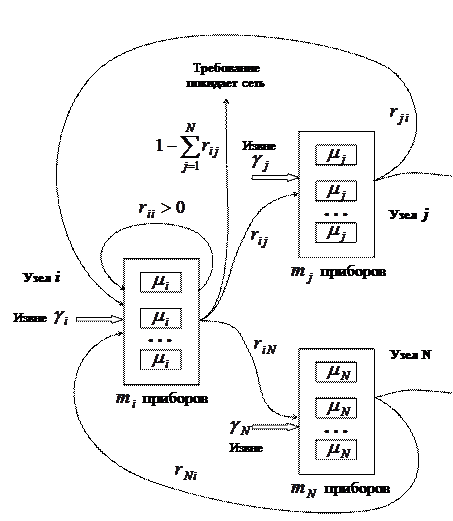
Этот вопрос для произвольной сети массового обслуживания исследовал Джексон. Он рассматривал сеть, содержащую N узлов, причем каждый i-й узел состоит из 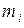 обслуживающих приборов с показательным временем обслуживания с параметром
обслуживающих приборов с показательным временем обслуживания с параметром 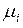 ; в каждый i-й узел извне поступает пуассоновский поток требований с интенсивностью
; в каждый i-й узел извне поступает пуассоновский поток требований с интенсивностью 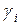 . Таким образом, при
. Таким образом, при 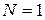 получаем обычную систему M/M/m. Покидая i-й узел, требование с вероятностью
получаем обычную систему M/M/m. Покидая i-й узел, требование с вероятностью 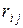 поступает в j-й узел, причем в формулировке задачи допускается, что
поступает в j-й узел, причем в формулировке задачи допускается, что 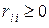 . С другой стороны, вероятность того, что после обслуживания в i-м узле требование покинет сеть (и никогда не вернется обратно), равна
. С другой стороны, вероятность того, что после обслуживания в i-м узле требование покинет сеть (и никогда не вернется обратно), равна 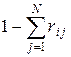 . Необходимо вычислить полную интенсивность потока требований в заданный узел. Для этого нужно просуммировать (пуассоновские) потоки, поступающие извне, и потоки требований (необязательно пуассоновские), поступающие от других узлов сети. Обозначая через
. Необходимо вычислить полную интенсивность потока требований в заданный узел. Для этого нужно просуммировать (пуассоновские) потоки, поступающие извне, и потоки требований (необязательно пуассоновские), поступающие от других узлов сети. Обозначая через  полную интенсивность потока, входящего в i-й узел, легко показать, что это множество параметров должно удовлетворять следующей системе уравнений:
полную интенсивность потока, входящего в i-й узел, легко показать, что это множество параметров должно удовлетворять следующей системе уравнений:
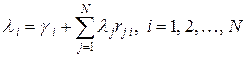 . (2)
. (2)
Для того, чтобы все узлы сети описывались эргодическими цепями Маркова, для всех i должно выполняться требование 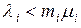 . Нужно снова предостеречь читателя от путаницы между понятием узла, используемом в данном обсуждении, и понятием состояния системы, которое ранее изображалось узлом графа. Самое удивительное состоит в том, что Джексон доказал, что каждый узел (скажем i-й) ведет себя в сети так, как если бы он был независимой системой M/M/m с входящим пуассоновским потоком с параметром
. Нужно снова предостеречь читателя от путаницы между понятием узла, используемом в данном обсуждении, и понятием состояния системы, которое ранее изображалось узлом графа. Самое удивительное состоит в том, что Джексон доказал, что каждый узел (скажем i-й) ведет себя в сети так, как если бы он был независимой системой M/M/m с входящим пуассоновским потоком с параметром  . В общем случае полный входящий поток не является пуассоновским.
. В общем случае полный входящий поток не является пуассоновским.
Выражение (1) получено с использованием преобразования Лапласа-Стилтьеса. Напомним, что существуют тесно связанные между собой преобразования для непрерывных случайных величин: характеристическая функция, производящая функция моментов и преобразование Лапласа-Стилтьеса.
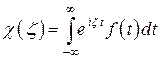 , (2)
, (2)
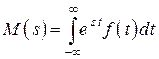 , (3)
, (3)
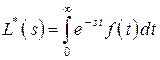 . (4)
. (4)
Характеристическая функция и производящая функция моментов связаны соотношением 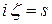 , производящая функция моментов отличается от преобразования Лапласа-Стилтьеса знаком у переменной s, а также пределами интегрирования, то есть преобразование Лапласа-Стилтьеса связывается только с положительными случайными величинами. Аналогом преобразования
, производящая функция моментов отличается от преобразования Лапласа-Стилтьеса знаком у переменной s, а также пределами интегрирования, то есть преобразование Лапласа-Стилтьеса связывается только с положительными случайными величинами. Аналогом преобразования
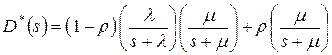
является эквивалентная производящая функция моментов
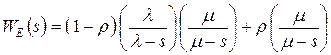 , (5)
, (5)
отражающая следующую GERT-сеть.
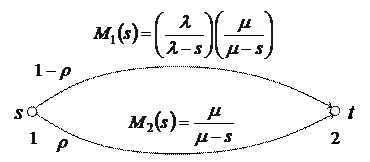 |
Логика получения этого выражения точно такая же, как и при получении формулы (1). В результате мы получаем
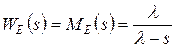 ,
,
а это эквивалентная производящая функция моментов экспоненциального распределения с параметром 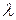 .
.
Но как убедиться в справедливости утверждения «исходящий поток стационарной СМО типа M/M/m с пуассоновским входящим потоком с параметром 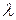 и показательным распределением времени обслуживания с параметром
и показательным распределением времени обслуживания с параметром 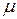 в каждом из m приборов является пуассоновским с тем же параметром
в каждом из m приборов является пуассоновским с тем же параметром 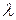 »?
»?
Рассмотрим стационарный режим СМО M/M/mс пуассоновским входящим потоком с параметром 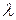 . Тогда выходной поток равен
. Тогда выходной поток равен 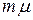 . Условием стационарности будет
. Условием стационарности будет 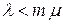 и по определению
и по определению 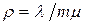 или
или  . Тогда стационарного режима СМО M/M/mполучаем следующую GERT-сеть
. Тогда стационарного режима СМО M/M/mполучаем следующую GERT-сеть
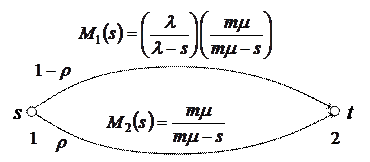 |
с эквивалентной W-функцией
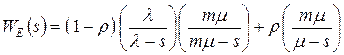 .
.
Преобразования выполняются аналогично ранее проделанным.
В самом деле 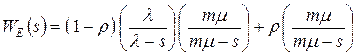 =
=
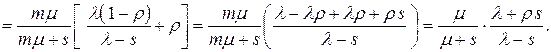
Выполняя подстановку 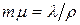 , получаем
, получаем
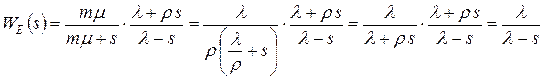 .
.
Или 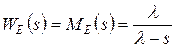 , что доказывает справедливость сделанного утверждения.
, что доказывает справедливость сделанного утверждения.
Теперь рассмотрим типовой случай, когда входной поток не является пуассоновским, но отдельный узел ведет себя как СМО M/M/mс пуассоновским входящим потоком с параметром 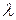 , о чем говорится в теореме Джексона.
, о чем говорится в теореме Джексона.
Рассмотрим СМО с обратной связью, в которой заявка, поступившая на выход системы с вероятностью 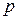 покидает ее, и с вероятностью
покидает ее, и с вероятностью 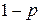 снова поступает на вход СМО (см. рисунок).
снова поступает на вход СМО (см. рисунок).
 |
Если интенсивность поступления заявок 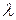 существенно меньше интенсивности обслуживания
существенно меньше интенсивности обслуживания 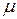 , тогда поведение системы достаточно хорошо описывается теоремой Джексона. Для объяснения поведения системы воспользуемся вспомогательной GERT-сетью, изображенной на рис. ниже.
, тогда поведение системы достаточно хорошо описывается теоремой Джексона. Для объяснения поведения системы воспользуемся вспомогательной GERT-сетью, изображенной на рис. ниже.
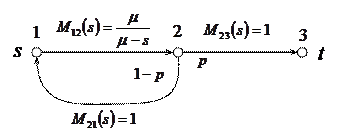 |
Дуга (1, 2) характеризует время обработки заявки в обслуживающем приборе (с интенсивностью 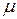 ). Дуга (2, 3) отражает передачу заявки на выход системы, а дуга (2, 1) отражает повторное поступление заявки на ее вход. Отметим, что эти действия чисто логические, то есть заявки передаются без задержки (с нулевым временем задержки) и поэтому дуги (1, 2) и (2, 3) характеризуются производящей функцией моментов
). Дуга (2, 3) отражает передачу заявки на выход системы, а дуга (2, 1) отражает повторное поступление заявки на ее вход. Отметим, что эти действия чисто логические, то есть заявки передаются без задержки (с нулевым временем задержки) и поэтому дуги (1, 2) и (2, 3) характеризуются производящей функцией моментов 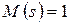 .
.
Необходимостью отражения задержек и объясняется переход от преобразований Лапласа-Стилтьеса к аппарату GERT-сетей с применением производящих функций моментов. Для нормального распределения не определено преобразование Лапласа-Стилтьеса, так как случайная величина, характеризующаяся нормальным распределением, может принимать и отрицательные значения. В то же время преобразование Лапласа-Стилтьеса существует только для положительных случайных величин. Производящая функция моментов нормального распределения 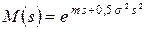 , где
, где 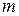 - математическое ожидание случайной величины, а
- математическое ожидание случайной величины, а 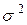 - ее дисперсия. Если мы имеем дело с постоянной величиной (в нашем случае с постоянной задержкой), то ее дисперсия равна 0 и
- ее дисперсия. Если мы имеем дело с постоянной величиной (в нашем случае с постоянной задержкой), то ее дисперсия равна 0 и 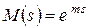 . Тогда при нулевой задержке
. Тогда при нулевой задержке 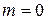 и
и 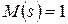 .
.
Упростим представленную GERT-сеть путем замены ее на эквивалентную сеть дублированием узла 2 (смотри рисунок ниже).
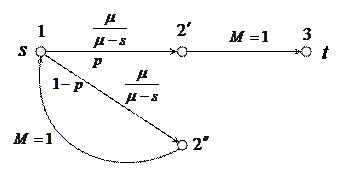 |
Заменяя последовательно соединенные дуги на эквивалентные, получаем более простую сеть.
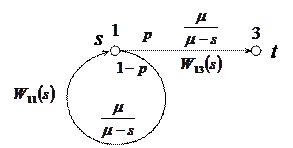 |
Найдем ее эквивалентную W-функцию.
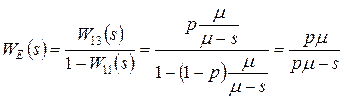 .
.
Среднее время обслуживания заявки
 .
.
Несмотря на то, что время обслуживания характеризовалось графовой структурой типа «дуга-петля», время обслуживания есть экспоненциальная случайная величина с параметром  . Напомним еще раз, что введено предположение о том, что
. Напомним еще раз, что введено предположение о том, что 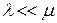 , для математической модели это можно интерпретировать, что все циклы по дуге (1,1) закончатся до прихода следующей заявки.
, для математической модели это можно интерпретировать, что все циклы по дуге (1,1) закончатся до прихода следующей заявки.
Если мы имеем простейший входной поток с интенсивностью 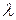 , а среднее время обслуживания заявки
, а среднее время обслуживания заявки 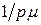 . При выполнении условия стационарного режима
. При выполнении условия стационарного режима 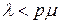 мы получаем модель для нахождения задержек
мы получаем модель для нахождения задержек
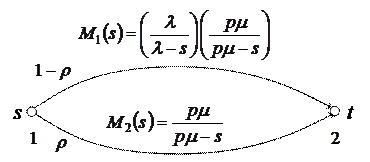 |
аналогичную модели для определения задержек в системе M/M/mс пуассоновским входящим потоком с параметром 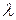 . Отличаются они только тем, что число обслуживающих устройств
. Отличаются они только тем, что число обслуживающих устройств 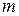 заменяется на вероятность выхода заявки из системы
заменяется на вероятность выхода заявки из системы 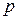 . Следует еще заметить, что последняя рассматриваемая нами СМО содержит в отличие от СМО M/M/mпетлю обратной связи.
. Следует еще заметить, что последняя рассматриваемая нами СМО содержит в отличие от СМО M/M/mпетлю обратной связи.
После замены 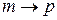 получаем выражение для эквивалентной W-функции интервала выхода заявок в рассматриваемой системе с обратной связью
получаем выражение для эквивалентной W-функции интервала выхода заявок в рассматриваемой системе с обратной связью
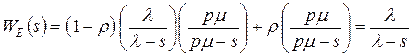 .
.
Это случайная величина с экспоненциальным распределением с параметром 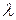 . И это притом, что, строго говоря, среднее время обслуживания не отвечает марковскому свойству (стационарности, ординарности и отсутствию последействия).
. И это притом, что, строго говоря, среднее время обслуживания не отвечает марковскому свойству (стационарности, ординарности и отсутствию последействия).
Рассмотрим процесс обслуживания более внимательно. Представим фрагмент «дуга-петля» в виде эквивалентного ациклического графа
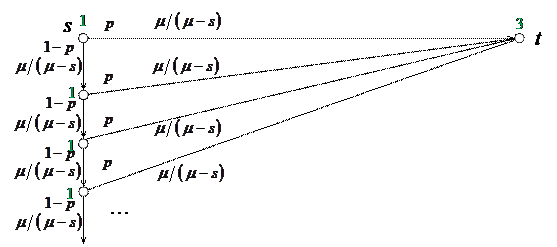 |
Дальнейшие эквивалентные преобразования заключаются в выделении параллельных ветвей
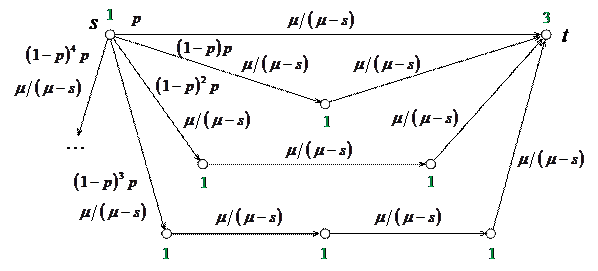 |
Следующий этап упрощений заключается в замене последовательно соединенных дуг на эквивалентные дуги.
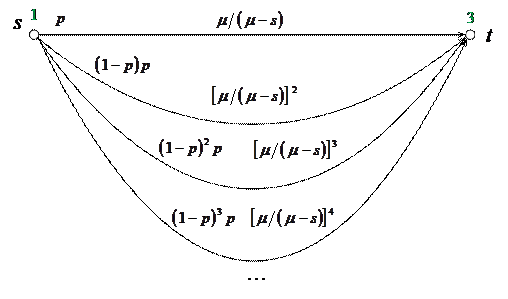 |
Теперь выполняется последнее эквивалентное преобразование – замена параллельных дуг на единственную эквивалентную
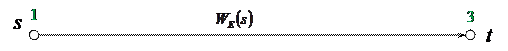 |
с эквивалентной W-функцией
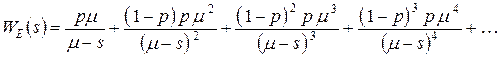 .
.
Так как отдельные слагаемые есть эквивалентные W-функции последовательно соединенных дуг, то они по абсолютной величине меньше 1. Тогда последнее выражение можно представить как геометрическую прогрессию
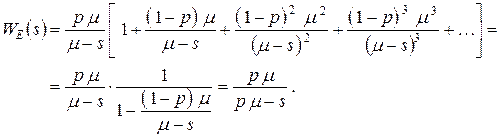
Таким образом, из приведенных выше ациклических диаграмм мы видим, что процесс обслуживания зависит от множества случайных величин, находящихся между собой в функциональной зависимости (суммы случайных величин и их вероятностные смеси). Из этого следует, что процесс обслуживания заявки свойством отсутствия последействия (марковским свойством) не обладает.
Тем не менее, если рассматривать данную СМО с обратной связью как «черный ящик», и анализировать ее поведение только в моменты ухода заявок из системы (при условии, что на нее поступает простейший поток заявок с интенсивностью 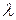 ), то мы видим, что интервалы меду выходами заявок заданы экспоненциальным распределением с параметром
), то мы видим, что интервалы меду выходами заявок заданы экспоненциальным распределением с параметром  . Тогда мы можем говорить о том, что процесс передачи заявок через данную СМО характеризуется вложенной марковской цепью.
. Тогда мы можем говорить о том, что процесс передачи заявок через данную СМО характеризуется вложенной марковской цепью.
Нужно помнить еще и о том, что должно выполняться условие стационарности 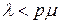 , а также то, что теорема Джексона будет удовлетворительно описывать систему только тогда, когда
, а также то, что теорема Джексона будет удовлетворительно описывать систему только тогда, когда 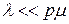 .
.
Состояние рассматриваемой системы с N узлами описывается вектором 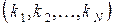 , где
, где 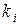 означает число требований в i-м узле (включая обслуживаемые требования). Обозначим через
означает число требований в i-м узле (включая обслуживаемые требования). Обозначим через 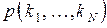 стационарную вероятность этого состояния. Аналогично, через
стационарную вероятность этого состояния. Аналогично, через 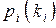 обозначим маргинальное (частное) распределение вероятностей того, что в состоянии равновесия в i-м узле будет находиться
обозначим маргинальное (частное) распределение вероятностей того, что в состоянии равновесия в i-м узле будет находиться 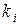 требований. Джексону удалось доказать, что совместное распределение по всем узлам разлагается в произведение маргинальных распределений, т. е. что
требований. Джексону удалось доказать, что совместное распределение по всем узлам разлагается в произведение маргинальных распределений, т. е. что
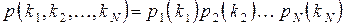 (3)
(3)
и что 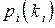 представляют собой стационарные вероятности для классической системы M/M/m.Этот последний результат обычно называют теоремой Джексона.
представляют собой стационарные вероятности для классической системы M/M/m.Этот последний результат обычно называют теоремой Джексона.
Модификация сети Джексона была исследована Гордоном и Ньюэллом. Исследованная ими модификация представляет собой замкнутую марковскую сеть в том смысле, что в системе рассматривается конечное и фиксированное число K требований, которые задерживаются в сети так, что ни одно из них не может покинуть сеть и ни одно другое требование не может поступить в нее; это соответствует теореме Джексона, в которой 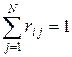 и
и 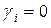 для всех i (интересный пример систем этого класса, известных под названием циклических, был рассмотрен Кенигсбергом; в циклической сети узлы последовательно связаны друг с другом, причем последний связан с первым). В общем случае, рассмотренном Гордоном и Ньюэллом, не приходится надеяться на решение в виде произведения, так как между компонентами вектора состояний
для всех i (интересный пример систем этого класса, известных под названием циклических, был рассмотрен Кенигсбергом; в циклической сети узлы последовательно связаны друг с другом, причем последний связан с первым). В общем случае, рассмотренном Гордоном и Ньюэллом, не приходится надеяться на решение в виде произведения, так как между компонентами вектора состояний 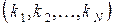 имеется следующая зависимость:
имеется следующая зависимость:
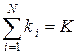 . (4)
. (4)
В этой модели множество состояний систем конечно: в частности, нетрудно видеть, что число различных состояний системы равно числу способов размещения K требований по N узлам.
