Постановка задачи. Для приближенной оценки изучаемых параметров будем использовать формулы классической и квантовой теорий свободных электронов

Для приближенной оценки изучаемых параметров будем использовать формулы классической и квантовой теорий свободных электронов.

Для определения средней длины свободного пробега электронов в металле используем упрощенную формулу, которая выводится на основе классических и квантовых представлений:

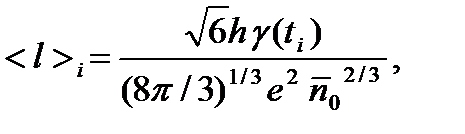(13)

где h – постоянная Планка, е – заряд электрона, 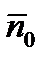- среднее число электронов в единице объема металла.

Средняя скорость теплового движения электрона <u>:

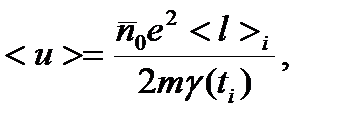(14)

Полученные значения 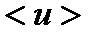и 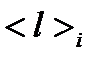дают возможность оценить время свободного пробега <τ>_i и частоту столкновений электронов <z>_i из следующих соотношений:

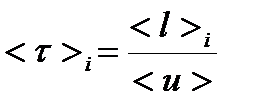, (15)

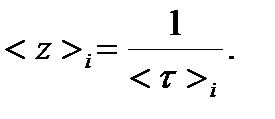(16)

Полное электрическое сопротивление складывается из идеального (чистый металл) и остаточного (примесного). Поэтому очень чувствительной характеристикой чистоты металла и совершенства кристаллической решетки является относительное остаточное сопротивление. На практике в паспортах указывается ρ₁₀₀/ρ₀ .

В данной части работы Вам следует ввести в ЭВМ исходные данные по прилагаемому образцу.

А. Входные величины: массивы измеренных сопротивлений R_i и соответствующих им температуры t_i .

Выходные величины:

1. Массивы оценок температурных зависимостей ρ(t_i), γ(t_i), <l>_i , <τ>_i, <z>_i , R(t_i)/R₀ .

2. Оценки средних значений физических величин для изучаемого интервала температур <u>, α, R₀ .

Модель «электронного газа» имеет ряд недостатков. В частности, эта модель не может объяснить электропроводность полупроводников. Последовательная теория электропроводности полупроводниковых материалов создана на основе квантовой механики – зонной теорией.

Рассмотрим собственный (беспримесный) полупроводник IV группы (Ge или Si). В кристаллической решетке атомы германия образуют ковалентную связь (рис. 2) – четыре валентных электрона осуществляют двойную связь со своими соседями. Так как все внешние электроны связаны, свободных электронов нет, поэтому при температуре Т = 0 К кристалл Ge является диэлектриком.

С увеличением температуры тепловые колебания решетки приводят к разрыву валентных связей, в результате часть электронов становятся потенциальными носителями электрического тока. Но когда электрон «отрывается» от кристаллической решетки и становится самостоятельным, то нарушается нейтральность решетки в том месте, откуда электрон «ушел». Появляется дефектное место – «дырка» (рис. 3а). «Дырка» определяется как квантовое состояние, не занятое электроном. Она ведет себя как положительный заряд, который может перемещаться по кристаллу (рис. 3б).

Таким образом, при температуре, отличной от абсолютного нуля, в кристалле беспримесного полупроводника появляется два типа носителей заряда – электроны и дырки. Концентрации этих носителей, очевидно, равны.

Проводимость химически чистых полупроводников называется собственной проводимостью, а сами полупроводники – собственными. Примером таких полупроводников могут служить химически чистый германий, кремний, селен, теллур и ряд химических соединений: арсенид галлия (GaAs), арсенид индия (InAS), карбид кремния (SiC) и т.д.

На рис. 4а показана упрощенная схема зонной структуры собственного полупроводника. При абсолютном нуле его валентная зона полностью (попарно) заполнена электронами в соответствии с принципом Паули, зона проводимости является пустой. С повышением температуры вследствие термического возбуждения электронов валентной зоны часть из них приобретает энергию, достаточную для преодоления запрещенной зоны и перехода в зону проводимости (рис. 4б).

Это приводит к появлению в зоне проводимости свободных электронов, а в валентной зоне – свободных уровней, на которые могут переходить электроны этой зоны. При приложении к такому кристаллу внешнего поля в нем возникает направленное движение электронов зоны проводимости и валентной зоны, приводящие к появлению электрического тока. Кристалл становится проводящим.

Чем уже запрещенная зона и выше температура кристалла, тем больше электронов переходит в зону проводимости, поэтому тем большую электропроводность приобретает кристалл. Так у германия, имеющего ΔЕ₀ = 0,66 эВ уже при комнатной температуре концентрация электронного газа в зоне проводимости достигает величины n_i = 10¹⁰ м^-3 и удельное сопротивление составляет ρ_i ≈ 0,48 Ом·м.

Температурная зависимость сопротивления полупроводника, обладающего собственной проводимостью, определяется формулой:

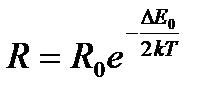, (17)

где k – постоянная Больцмана, ΔE₀ – ширина запрещенной зоны, Т – абсолютная температура, R₀ – постоянная, характерная для данного полупроводника.

После логарифмирования (17) получаем уравнение прямой линии в координатах lnR и 1/T :

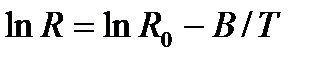, (18)

где 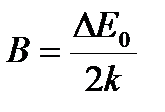. Из (18) следует:

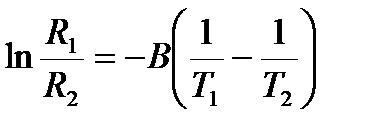. (19)

Тогда 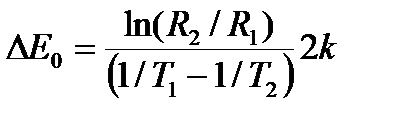. (20)

Температурный коэффициент сопротивления материала терморезистора определяется по формуле:

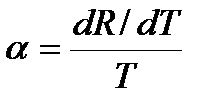. (21)