Динамика переходных процессов ненагруженных машин

Переходные процессы (пуск и остановка) многих машин (прокатные станы, ножницы, металлургические станки и т.п.) проходят при отсутствии внешних сопротивлений. Однако в момент пуска и остановки холостой машины её элементы испытывают динамические нагрузки.

Дифференциальные уравнения движения двухмассовой системы (рис. 16) запишем в виде

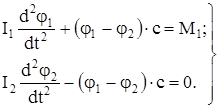(122)

Здесь ;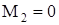

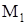– момент, создаваемый двигателем в период пуска или тормозной – в период остановки.

Умножим первое уравнение на I₂, а второе на I₁ и вычтем второе из первого. После преобразований получим одно уравнение

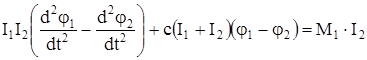. (123)

Заменяя 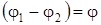и преобразуя, найдем

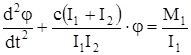, (124)

или

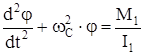. (125)

Общее решение этого уравнения имеет вид

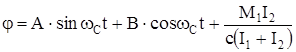. (126)

Примем начальные условия: при .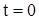

Тогда

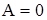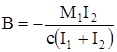, . (127)

После подстановки значений коэффициентов A и B в (126) получим

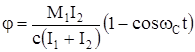. (128)

Текущее значение момента в упругой связи

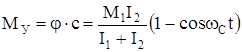. (129)

Максимальная деформация упругого звена будет в момент времени, соответствующий значению 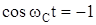, т.е.

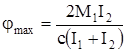, (130)

а максимальный динамический момент в упругом звене

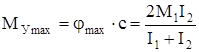. (131)

Формула (131) справедлива для разгона и торможения системы, если тормозной момент прикладывается к ведущей массе (например, вал электродвигателя). В случае, когда момент торможения приложен к ведомой массе, формула имеет вид

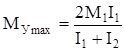. (132)

Динамика переходных процессов нагруженных машин

Пуск и остановка многих машин (мостовые краны, различные грузоподъемные устройства, скиповые подъемники и т.п.) осуществляются при наличии внешних нагрузок. Рассмотрим несколько случаев, характеризующихся разным характером приложения внешних нагрузок.

Мгновенное приложение нагрузки

Примером такого приложения нагрузки является подъем груза «с подрывом» (рис. 17).

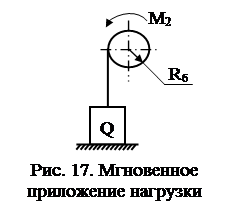Дифференциальные уравнения движения системы при пуске

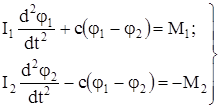. (133)

В результате решения системы уравнений (133) для начальных условий 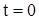, 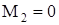получим

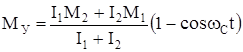, (134)

где

,

.

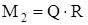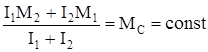Тогда

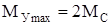, (135)

а коэффициент динамичности

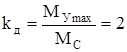. (136)

Пуск при постоянной нагрузке

Примером такого характера приложения нагрузки является подъем груза из промежуточного положения (рис. 18).

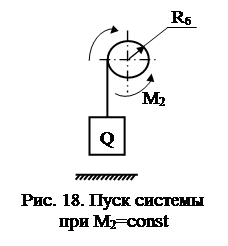Решая систему уравнений (133) получим

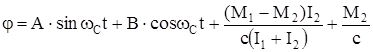. (137)

Отсчитывая время от начала движения обеих масс системы, т.е. полагая, что пр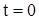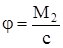и и 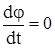, и подставляя эти условия в уравнение (137), получим

; .

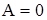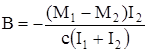Тогда

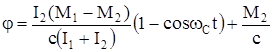. (138)

Момент, воспринимаемый упругим звеном

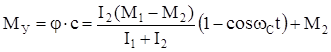, (139)

а его максимальное значение

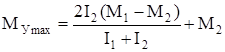. (140)

При торможении системы тормозящий момент может быть приложен к ведущей или ведомой массам.

В первом случае момент торможения и момент нагрузки M₂ имеют одинаковый знак. Поэтому в начальных условиях следует принять, что для 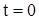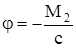. Тогда

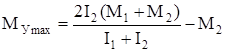. (141)

Во втором случае в первом из уравнений (133) следует правую часть приравнять нулю, а во втором уравнении правая часть будет .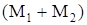

При этом

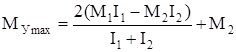. (142)