Низшие уровни описания систем

Высшие уровни описания систем.

Лингвистический уровень описания - наиболее высокий уровень абстрагирования. Из него как частные случаи можно получить другие уровни абстрактного описания систем более низкого ранга. Предназначен для формализации объекта, т.е. на этом уровне выбирается язык описания объекта, а так же построение модели реального объекта для дальнейших манипуляций с ней.

Ценность лингвистического описания системы состоит в установлении неформализованных структурных элементов системы и связей между ними. Все высказывания делят обычно на два типа. К первому причисляют «термы» (имена предметов, члены предложения и т. д.) – высказывания, с помощью которых обозначают объекты исследования, а ко второму – «функторы» – высказывания, определяющие отношения между термами (например А=В).

С помощью термов и функторов можно показать, как из лингвистического уровня абстрактного описания (уровня высшего ранга) как частный случай возникает теоретико-множественный уровень абстрагирования (уровень более низкого ранга).

Элементы при формализации называются конституэнтами, которые только при определенном значении делают высказывания верными.

На теоретико-множественном уровне абстракции можно получить только общие сведения о реальных системах, а для более конкретных целей необходимы другие абстрактные модели.

Если связи между элементами рассматриваемых множеств устанавливаются с помощью некоторых однозначных функций, отображающих элементы множества в само исходное множество, то приходим к абстрактно-алгебраическому уровню описания систем. В таких случаях говорят, что между элементами множеств установлены бинарные (двойственные) отношения.

Если же на элементах рассматриваемых множеств определены некоторые топологические структуры, то в этом случае приходим к топологическому уровню абстрактного описания систем.

Низшие уровни описания систем.

Логико-математический уровень описания систем нашел широкое применение для: формализации функционирования автоматов; задания условий функционирования автоматов; изучения вычислительной способности автоматов.

Понятие «автомат» имеет следующие значения:

1) устройство, выполняющее некоторый процесс без непосредственного участия человека. Применение автоматов значительно повышает производительность труда, скорость и точность выполнения операций. Освобождает человека от утомительного однообразного труда, для защиты человека от условий, опасных для жизни или вредных для здоровья. Автоматы используются там, где невозможно присутствие человека (высокая температура, давление, ускорение, вакуум и т. д.);

2) математическое понятие, математическая модель реальных (технических) автоматов. Абстрактно автомат можно представить как некоторое устройство («черный ящик»), имеющее конечное число входных и выходных каналов и некоторое множество внутренних состояний. На входные каналы извне поступают сигналы, и в зависимости от их значения и от того, в каком состоянии он находился, автомат переходит в следующее состояние и выдает сигналы на свои выходные каналы. С течением времени входные сигналы изменяются, соответственно изменяются и состояние автомата, и его выходные каналы. Таким образом, автомат функционирует во времени;

3) в узком смысле автомат употребляется для обозначения так называемых синхронных дискретных автоматов. Такие автоматы имеют конечные множества значений входных и выходных сигналов, называемых входным и выходным алфавитом. Время разбивается на промежутки одинаковой длительности (такты): на протяжении всего такта входной сигнал, состояние и выходной сигнал не изменяются. Изменения происходят только на границах тактов. Следовательно, время можно считать дискретным t=1,2,...,n.

При любом процессе управления или регулирования, осуществляемом живым организмом или автоматически действующей машиной либо устройством, происходит переработка входной информации в выходную. Поэтому при теоретико-информационном уровне абстрактного описания систем информация выступает как свойство объектов и явлений (процессов) порождать многообразие состояний, которые посредством отражения передаются от одного объекта к другому и запечатлеваются в его структуре (возможно, в измененном виде).

Динамический уровень абстрактного описания систем связан с представлением системы как некоторого объекта, куда в определенные моменты времени можно вводить вещество, энергию и информацию, а в другие моменты времени – выводить их, т. е. динамическая система наделяется свойством иметь «входы» и «выходы», причем процессы в них могут протекать как непрерывно, так и в дискретные моменты времени. Кроме этого, для динамических систем вводится понятие «состояние системы», характеризующее ее внутреннее свойство.

Эвристический уровень абстрактного описания систем предусматривает поиски удовлетворительного решения задач управления в связи с наличием в сложной системе человека. Эврика – это догадка, основанная на общем опыте решения родственных задач. Изучение интеллектуальной деятельности человека в процессе управления имеет очень важное значение.

Эвристика вообще – это прием, позволяющий сокращать количество просматриваемых вариантов при поиске решения задачи. Причем этот прием не гарантирует наилучшее решение.

Большое внимание сейчас уделяется созданию искусственного и гибридного интеллекта. При этом важное значение имеет решение проблемы иерархически организованного перебора, создание и разработка методов отсечения заведомо невыгодных путей.

Таким образом, обзор уровней абстрактного описания систем показывает, что выбор подходящего метода формального описания при изучении той или иной реальной системы является всегда наиболее ответственным и трудным шагом в теоретико-системных построениях. Эта часть исследования почти не поддастся формализации и во многом зависит от эрудиции исследователя, его профессиональной принадлежности, целей исследования и т. д.

Наибольшее значение в настоящее время в абстрактной теории систем придается теоретико-множественному, абстрактно-алгебраическому и динамическому уровням описания систем.

Кибернетический подход к описанию систем. Управление как процесс.

Кибернетический подход к описанию систем состоит в том, что всякое целенаправленное поведение рассматривается как управление. Управление — в широком, кибернетическом смысле — это обобщение приемов и методов, накопленных разными науками об управлении искусственными объектами и живыми организмами. Язык управления — это использование понятий «объект», «среда», «обратная связь», «алгоритм» и т.д.

Под управлением будем понимать процесс организации такого целенаправленного воздействия на некоторую часть среды, называемую объектом управления, в результате которого удовлетворяются потребности субъекта, взаимодействующего с этим объектом.

Анализ управления заставляет выделить тройку — среду, объект и субъект, внутри которой разыгрывается процесс управления. В данном случае субъект ощущает на себе воздействие среды Х и объекта У. Если состояние среды Х он изменить не может, то состоянием объекта У он может управлять с помощью специально организованного воздействия U. Это и есть управление. 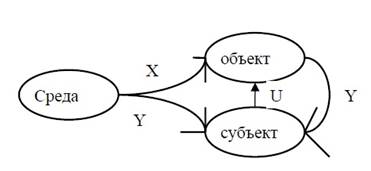Рис 2.1

Состояние объекта Y влияет на состояние потребностей субъекта. Потребности субъекта где — состояние i-й потребности субъекта, которая выражается неотрицательным числом, характеризующим насущность, актуальность этой потребности. Свое поведение субъект строит так, чтобы минимизировать насущность своих потребностей, т. е. решает задачу многокритериальной оптимизации (A_k=( α…α1), α_i - состояние i-й потребности субъекта), которая выражается неотрицательным числом, характеризующим насущность, актуальность этой потребности. Свое поведение субъект строит так, чтобы минимизировать насущность своих потребностей.

Пусть U_x^* решение задачи (2.1), т. е. оптимальное поведение субъекта, минимизирующее его потребности А. Способ решения задачи (2.1), позволяющий определить U_x^*, называется алгоритмом управления.

U_x^*=ϕ ( At, X), (2.2)

где ϕ — алгоритм, позволяющий синтезировать управление по состоянию среды Х и потребностей А_t,. Потребности субъекта изменяются не только под влиянием среды или объекта, но и самостоятельно, отражая жизнедеятельность субъекта, что отмечается индексом t.

Алгоритм управления ϕ₁, которым располагает субъект, и определяет эффективность его функционирования в данной среде. Алгоритм имеет рекуррентный характер:

U_N+1=ϕ(U_N, A_t, X), т. е. позволяет на каждом шаге улучшать управление.

Процесс управления как организация целенаправленного воздействия на объект может реализовываться как на интуитивном, так и на осознанном уровне. Первый используют животные, второй — человек. Осознанное удовлетворение потребностей заставляет декомпозировать алгоритм управления и вводить промежуточную стадию — формулировку цели управления, т.е. действовать по схеме Потребность – Цель – Оптимальное управление (П-Ц 1 этап, Ц-ОУ 2 этап). Именно на втором этапе синтезируется ϕ_2, который и является объектом изучения кибернетики как науки.

Процесс управления — это информационный процесс, заключающийся в сборе информации о ходе процесса, передаче ее в пункты накопления и переработки, анализе поступающей, накопленной и справочной информации, принятии решения на основе выполненного анализа, выработке соответствующего управляющего воздействия и доведении его до объекта управления. Каждая фаза процесса управления протекает во взаимодействии с окружающей средой при воздействии различного рода помех. Цели, принципы и границы управления зависят от сущности решаемой задачи.

Система управления — совокупность взаимодействующих между собой объекта управления и органа управления, деятельность которых направлена заданной цели управления

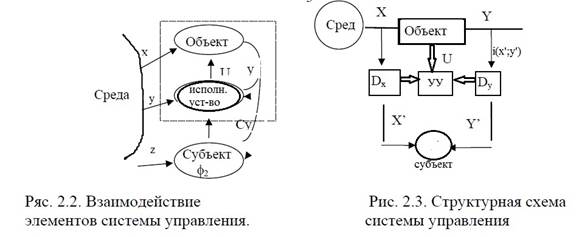
Dx,Dy – датчики состояния среды и объекта, x’,y’ – результаты измерения i(x’,y’) – исходная информация для принятия решений.

Этапы управления информационным процессом:

1. Формирование цепей. Множество целей управления, которое должно реализовать СУ определяется как внешними по отношению к системе, так и внутренними факторами и, в частности, потребностям субъекта А. Сложность формализации учета влияния на цели очевидна.

2. Определение объекта управления. Этот этап связан с выделением той части среды субъекта, состояние которой он может изменить и тем самым воздействовать на свои потребности. В ряде случаев, когда границы объекта очевидны, проблемы выделения объекта из среды не возникает. Это бывает, когда объект достаточно автономен (самолет, телефонная станция и т. д.). Однако в других случаях связи объекта со средой настолько сильны и разнообразны, что порой очень трудно понять, где кончается объект и начинается среда. Именно это и заставляет вводить специальный этап — определение объекта управления. Объект должен быть в определенном смысле минимальным, т. е. иметь наименьший объем. Это необходимо с целью минимизации трудоемкости его изучения при синтезе модели.

3. Структурный синтез модели. Последующие три этапа управления сложными системами связаны с решением задачи создания ее модели, которая нужна для синтеза управления U.

4. Идентификация параметров модели объекта. Этот этап связан с определением числовых значений параметров С в режиме нормального функционирования объекта. Делается это стандартными приемами идентификации. Для выяснения зависимости выхода объекта от управляемых входов

5. Планирование эксперимента. На данном этане главным является синтез плана эксперимента, позволяющего с максимальной эффективностью определить искомые параметры модели объекта управления. Для статического объекта этот план представляет собой набор состояний управляемого выхода объекта, а для динамического — план-функцию, т. е. программу изменения во времени входа объекта. Эксперимент на объекте дает возможность определить реакцию объекта на это воздействие.

6. Синтез управления. На этом этапе принимается решение о том, каково должно быть управление, чтобы достигнуть заданной цели управления в объекте. Это решение опирается на имеющуюся модель объекта (F), заданную цель (Z*), полученную информацию о состоянии среды (Х) и выделенный ресурс управления (R), который представляет собой ограничения, накладываемые на управление (U) в связи со спецификой объекта и возможностями СУ. Достижение цели Z* возможно соответствующим выбором управления U (состояние среды Х изменяется независимо от нас).

7. Реализация управления или отработка в объекте оптимального решения U*, полученного на предыдущем этапе. Реализовав управление и убедившись, что цель управления не достигнута, возвращаются к одному из предыдущих этапов. Даже в лучшем случае, когда поставленная цель достигнута, необходимость обращения к предыдущему этапу вызывается изменением состояния среды Х или сменой цели управления U*. Таким образом, при благоприятном стечении обстоятельств обращаются к этапу синтеза управления, где определяется новое состояние, которое отражает новую ситуацию, сложившуюся в среде. Так функционирует стандартный контур управления простым объектом.

8. Адаптация. Специфика управления сложной системой состоит в том, что благодаря зашумленности и нестационарности информация, полученная на предыдущих этапах, приближенно отражает состояние системы лишь в предыдущие моменты времени. Это и вызывает необходимость коррекции.

Очевидно, что не все из описанных выше восьми этапов управления присутствуют при синтезе СУ. В ряде случаев некоторые из них выпадают. Например, объект управления может быть выделен из среды и тогда нет необходимости в этапе планирования эксперимента, так как модель объекта проста и все ее параметры можно определить без специально организованного эксперимента.

Классификация видов моделирования систем

Моделирование–процесс исследования реальной системы, включающий построение модели, изучение ее свойств и перенос полученных сведений на моделируемую систему.

Модель – это некоторый материальный или абстрактный объект, находящийся в определенном объективном соответствии с исследуемым объектом, несущий о нем определенную информацию и способный его замещать на определенных этапах познания.

В соответствии с классификационным признаком полноты моделирование делится на: полное, неполное, приближенное.

При полном моделировании модели идентичны объекту во времени и пространстве.

Для неполного моделирования эта идентичность не сохраняется.

В основе приближенного моделирования лежит подобие, при котором некоторые стороны реального объекта не моделируются совсем. Теория подобия утверждает, что абсолютное подобие возможно лишь при замене одного объекта другим точно таким же. Поэтому при моделировании абсолютное подобие не имеет места. Исследователи стремятся к тому, чтобы модель хорошо отображала только исследуемый аспект системы. Например, для оценки помехоустойчивости дискретных каналов передачи информации функциональная и информационная модели системы могут не разрабатываться. Для достижения цели моделирования вполне достаточна событийная модель, описываемая матрицей условных вероятностей переходов i-го символа алфавита в j-й.

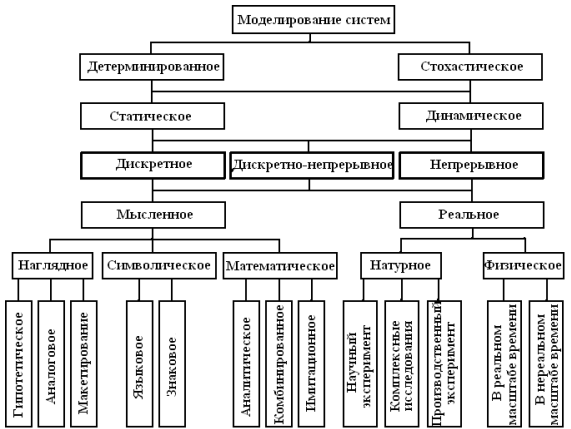
В зависимости от типа носителя и сигнатуры модели различаются следующие виды моделирования: детерминированное и стохастическое, статическое и динамическое, дискретное, непрерывное и дискретно-непрерывное.

Детерминированное моделирование отображает процессы, в которых предполагается отсутствие случайных воздействий.

Стохастическое моделирование учитывает вероятностные процессы и события.

Статическое моделирование служит для описания состояния объекта в фиксированный момент времени, а динамическое — для исследования объекта во времени. При этом оперируют аналоговыми (непрерывными), дискретными и смешанными моделями.

В зависимости от формы реализации носителя и сигнатуры моделирование классифицируется на мысленное и реальное.

Мысленное моделирование применяется тогда, когда модели не реализуемы в заданном интервале времени либо отсутствуют условия для их физического создания (например, ситуация микромира). Мысленное моделирование реальных систем реализуется в виде наглядного, символического и математического. Для представления функциональных, информационных и событийных моделей этого вида моделирования разработано значительное количество средств и методов.

При наглядном моделировании на базе представлений человека о реальных объектах создаются наглядные модели, отображающие явления и процессы, протекающие в объекте. Примером таких моделей являются учебные плакаты, рисунки, схемы, диаграммы.

В основу гипотетического моделирования закладывается гипотеза о закономерностях протекания процесса в реальном объекте, которая отражает уровень знаний исследователя об объекте и базируется на причинно-следственных связях между входом и выходом изучаемого объекта. Этот вид моделирования используется, когда знаний об объекте недостаточно для построения формальных моделей. Аналоговое моделирование основывается на применении аналогий различных уровней. Для достаточно простых объектов наивысшим уровнем является полная аналогия. С усложнением системы используются аналогии последующих уровней, когда аналоговая модель отображает несколько (или только одну) сторон функционирования объекта.

Макетирование применяется, когда протекающие в реальном объекте процессы не поддаются физическому моделированию или могут предшествовать проведению других видов моделирования. В основе построения мысленных макетов также лежат аналогии, обычно базирующиеся на причинно-следственных связях между явлениями и процессами в объекте.

Символическое моделирование представляет собой искусственный процесс создания логического объекта, который замещает реальный и выражает его основные свойства с помощью определенной системы знаков и символов.

В основе языкового моделирования лежит некоторый тезаурус, который образуется из набора понятий исследуемой предметной области, причем этот набор должен быть фиксированным. Под тезаурусом понимается словарь, отражающий связи между словами или иными элементами данного языка, предназначенный для поиска слов по их смыслу.

Традиционный тезаурус состоит из двух частей: списка слов и устойчивых словосочетаний, сгруппированных по смысловым (тематическим) рубрикам; алфавитного словаря ключевых слов, задающих классы условной эквивалентности, указателя отношений между ключевыми словами, где для каждого слова указаны соответствующие рубрики. Такое построение позволяет определить семантические (смысловые) отношения иерархического (род/вид) и неиерархического (синонимия, антонимия, ассоциации) типа.

Между тезаурусом и обычным словарем имеются принципиальные различия. Тезаурус — словарь, который очищен от неоднозначности, т.е. в нем каждому слову может соответствовать лишь единственное понятие, хотя в обычном словаре одному слову может соответствовать несколько понятий.

Если ввести условное обозначение отдельных понятий, т.е. знаки, а также определенные операции между этими знаками, то можно реализовать знаковое моделирование и с помощью знаков отображать набор понятий — составлять отдельные цепочки из слов и предложений. Используя операции объединения, пересечения и дополнения теории множеств, можно в отдельных символах дать описание какого-то реального объекта.

Математическое моделирование — это процесс установления соответствия данному реальному объекту некоторого математического объекта, называемого математической моделью. В принципе, для исследования характеристик любой системы математическими методами, включая и машинные, должна быть обязательно проведена формализация этого процесса, т.е. построена математическая модель. Вид математической модели зависит как от природы реального объекта, так и от задач исследования объекта, от требуемой достоверности и точности решения задачи. Любая математическая модель, как и всякая другая, описывает реальный объект с некоторой степенью приближения. При реальном моделировании используется возможность исследования характеристик либо на реальном объекте целиком, либо на его части. Такие исследования проводятся как на объектах, работающих в нормальных режимах, так и при организации специальных режимов для оценки интересующих исследователя характеристик (при других значениях переменных и параметров, в другом масштабе времени и т.д.). Реальное моделирование является наиболее адекватным, но его возможности ограничены.

Натурным моделированием называют проведение исследования на реальном объекте с последующей обработкой результатов эксперимента на основе теории подобия.

Другим видом реального моделирования является физическое, отличающееся от натурного тем, что исследование проводится а установках, которые сохраняют природу явлений и обладают физическим подобием. В процессе физического моделирования задаются некоторые характеристики внешней среды и исследуется поведение либо реального объекта, либо его модели при заданных или создаваемых искусственно воздействиях внешней среды.

Имитационное моделирование систем

Одним из методов исследования сложных систем, в том числе, и систем массового обслуживания является метод имитационного моделирования, когда модель имитирует работу реальной системы, т.е. модель воспроизводит процесс функционирования реальной системы во времени.

Любая система, как известно, представляет собой совокупность взаимосвязанных элементов и, следовательно, построение ее адекватной имитационной модели предполагает имитацию процесса функционирования каждого отдельного элемента системы с обязательным сохранением логики и правил взаимодействия и развития составляющих систему элементов, как во времени, так и в пространстве (в том числе последовательность и параллелизм их во времени).

Основное преимущество имитационного моделирования перед другими видами моделирования (например, аналитическим) состоит в универсальности в смысле возможности исследования любых достаточно сложных систем, с учетом таких факторов и условий, которые трудно или вообще невозможно учитывать при аналитическом моделировании. Поэтому во многих случаях имитационное моделирование становится наиболее эффективным, а часто и практически единственно доступным методом исследования систем. Например, результативный анализ систем массового обслуживания аналитическими методами невозможен, в то время как такой анализ методами имитационного моделирования не представляет особой сложности.

При исследовании систем со стохастическим характером функционирования (системы массового обслуживания являются системами такого типа) результаты, полученные при единичном "прогоне" имитационной модели (при единичном воспроизведении на имитационной модели процесса функционирования системы), носят частный характер. Следовательно, для того, чтобы найти одну оценку (одно значение) какой-либо характеристики функционирования системы необходимо многократно "прогонять" имитационную модель (необходимо получить множество результатов) с последующей статистической обработкой полученных данных. Поэтому в имитационной модели должны быть предусмотрены средства сбора и средства последующей статистической обработки данных, полученных в ходе моделирования по интересующим характеристикам системы. Например, моделирование случайной величины Y, распределенной по экспоненциальному закону с параметром l, предполагает выполнение следующих действий:

1) розыгрыш равномерно распределенного случайного числа xÎ[0,w];

2) определение соответствующего значения .

Единичная реализация этой элементарной имитационной модели из двух действий дает одно значение случайной величины Y. Если задача (цель) моделирования состоит в оценке среднего значения , то необходимо добавить в модель дополнительное (третье) действие S = S + y для накопления суммы случайных величин (средство сбора) и многократно реализовать полученную модель. В конце моделирования в качестве оценки для принять отношение S/N (средство обработки), где N — общее число реализаций модели.

Если необходимо построить (найти) функциональную зависимость среднего значения, например, от параметра l, то для множества точек этой зависимости нужно проделать каждый раз всю описанную выше процедуру моделирования, сбора и обработки данных. Даже в такой простой задаче очевидным образом проявляется присущий имитационному моделированию недостаток — это его трудоемкость.

Ситуационное моделирование систем

Ситуационное моделирование относится к математическому моделированию

Математическое моделирование — это процесс установления соответствия данному реальному объекту некоторого математического объекта, называемого математической моделью. В принципе, для исследования характеристик любой системы математическими методами, включая и машинные, должна быть обязательно проведена формализация этого процесса, т.е. построена математическая модель. Вид математической модели зависит как от природы реального объекта, так и от задач исследования объекта, от требуемой достоверности и точности решения задачи. Любая математическая модель, как и всякая другая, описывает реальный объект с некоторой степенью приближения.

Ситуационное моделирование опирается на модельную теорию мышления, в рамках которой можно описать основные механизмы регулирования процессов принятия решений. В центре модельной теории мышления лежит представление о формировании в структурах мозга информационной модели объекта и внешнего мира. Эта информация воспринимается человеком на базе уже имеющихся у него знаний и опыта. Целесообразное поведение человека строится путем формирования целевой ситуации и мысленного преобразования исходной ситуации в целевую. Основой построения модели является описание объекта в виде совокупности элементов, связанных между собой определенными отношениями, отображающими семантику предметной области. Модель объекта имеет многоуровневую структуру и представляет собой тот информационный контекст, на фоне которого протекают процессы управления. Чем богаче информационная модель объекта и выше возможности манипулирования ею, тем лучше и многообразнее качество принимаемых решений при управлении.

Системно-структурное моделирование систем

Структурное моделирование системного анализа базируется на некоторых специфических особенностях структур определенного вида, которые используются как средство исследования систем или служат для разработки на их основе специфических подходов к моделированию с применением других методов формализованного представления систем (теоретико-множественных, лингвистических, кибернетических и т.п.).

Структурное моделирование системного анализа включает:

· методы сетевого моделирования;

· сочетание методов структуризации с лингвистическими;

· структурный подход в направлении формализации построения и исследования структур разного типа (иерархических, матричных, произвольных графов) на основе теоретико-множественных представлений и понятия номинальной шкалы теории измерений.

При этом термин «структура модели» может применяться как функциям, так и к элементам системы. Соответствующие структуры называются функциональными и морфологическими. Объектно-ориентированное моделирование объединяет структуры обоих типов в иерархию классов, включающих как элементы, так и функции.

В структурном моделировании за последнее десятилетие сформировалась новая технология CASE. Аббревиатура CASE имеет двоякое толкование, соответствующее двум направлениям использования CASE-систем. Первое из них — Computer-Aided Software Engineering — переводится как автоматизированное проектирование программного обеспечения. Соответствующие CASE-системы часто называют инструментальными средами быстрой разработки программного обеспечения. Второе — Computer-Aided System Engineering — подчеркивает направленность на поддержку концептуального моделирования сложных систем, преимущественно слабоструктурированных. Такие CASE-системы часто называют системами BPR (Business Process Reengineering). В целом CASE-технология представляет собой совокупность методологий анализа, проектирования, разработки и сопровождения сложных автоматизированных систем, поддерживаемую комплексом взаимосвязанных средств автоматизации. CASE — это инструментарий для системных аналитиков, разработчиков и программистов, позволяющий автоматизировать процесс проектирования и разработки сложных систем, в том числе и программного обеспечения.

Информационное моделирование систем

Информационное (кибернетическое) моделирование связано с исследованием моделей, в которых отсутствует непосредственное подобие физических процессов, происходящих в моделях, реальным процессам. В этом случае стремятся отобразить лишь некоторую функцию, рассматривают реальный объект как «черный ящик», имеющий ряд входов и выходов, и моделируют некоторые связи между выходами и входами. Таким образом, в основе информационных (кибернетических) моделей лежит отражение некоторых информационных процессов управления, что позволяет оценить поведение реального объекта. Для построения модели в этом случае необходимо выделить исследуемую функцию реального объекта, попытаться формализовать эту функцию в виде некоторых операторов связи между входом и выходом и воспроизвести данную функцию на имитационной модели, причем на совершенно другом математическом языке и, естественно, иной физической реализации процесса. Так, например, экспертные системы являются моделями ЛПР.

Для более подробного ответа смотри на схему и описание «Классификации видов методов моделирования систем»

Математическое моделирование систем

Математическое моделирование — это процесс установления соответствия данному реальному объекту некоторого математического объекта, называемого математической моделью. В принципе, для исследования характеристик любой системы математическими методами, включая и машинные, должна быть обязательно проведена формализация этого процесса, т.е. построена математическая модель. Вид математической модели зависит как от природы реального объекта, так и от задач исследования объекта, от требуемой достоверности и точности решения задачи. Любая математическая модель, как и всякая другая, описывает реальный объект с некоторой степенью приближения.

Для более подробного ответа смотри на схему и описание «Классификации видов методов моделирования систем»

Описание системы в теоретико-множественных терминах

Вводятся основные понятия теории систем на теоретико-множественном уровне и устанавливаются взаимосвязи между ними. Система определяется прежде всего как некоторое отношение на абстрактных множествах, а затем дается оценивание временных и динамических систем как систем на множествах абстрактных функций времени. Для того чтобы иметь возможность определять системы различных типов более конкретно, вводятся вспомогательные функции и объекты, такие, как состояние, глобальное состояние, глобальная реакция системы.

Желая получить математическую модель процесса функционирования системы, чтобы она охватывала широкий класс реальных объектов, в общей теории систем исходят из общих предположений о характере функционирования системы:

1) система функционирует во времени; в каждый момент времени система может находиться в одном из возможных состояний;

2) на вход системы могут поступать входные сигналы;

3) система способна выдавать выходные сигналы;

4) состояние системы в данный момент времени определяется предыдущими состояниями и входными сигналами, поступившими в данный момент времени и ранее;

5) выходной сигнал в данный момент времени определяется состояниями системы и входными сигналами, относящимися к данному и предшествующим моментам времени.

Первое из перечисленных предположений отражает динами­ческий характер процесса функционирования в пространстве и времени. При этом процесс функционирования протекает как последовательная смена состояний системы под действием внешних и внутренних причин.

Второе и третье предположения отражают взаимодействие системы с внешней средой.

В четвертом и пятом предположениях отражается реакция системы на внутренние факторы и воздействия внешней среды:

Последний принцип физической реализуемости. Многим явлениям и процессам свойственно последействие, вследствие которого тенденции, определяющие поведение системы в буду­щем, зависят не только от того, в каком состоянии находится система в настоящий момент времени, но в той или иной степени от ее поведения в предыдущие моменты времени (например, усвоение студентом сложных дисциплин — теории систем, те­ории построения АСУ, исследования операций, теории массового обслуживания и др. — зависит от степени усвоения курса теории вероятностей и математической статистики, а еще дальше — от знания курса высшей математики).

Принцип физической реализуемости заключается в следу­ющем: система не реагирует в данный момент времени на «буду­щие» факторы и воздействия внешней среды.

Одним из центральных понятий теории систем является поня­тие системы, определенное в теоретико-множественных терминах:

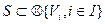где V, — вес компоненты; iÎI — декартова произведения ÄV_i , называемые объектами системы S; I — множество индексов. В кибернетике наибольший интерес представляют системы с дву­мя объектами — входным объектом X и выходным объектом Y:

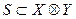Основными причинами определения системы как теоретико-множественного отношения являются следующие:

1. Система определяется в терминах ее наблюдаемых свойств или, точнее говоря, в терминах взаимосвязей между этими свой­ствами, а не тем, что они на самом деле собой представляют (т. е. не с помощью физических, химических, биологических, социа­льных или других явлений). Это вполне согласуется с природой системных исследований, направленных на выяснение организа­ции и взаимосвязи элементов системы, а не на изучение конкрет­ных механизмов в системе.

2. Определение системы как отношения вида (3.1) является предельно общим. Конечно, различным системам отвечают и различные способы задания описания (дифференциальные урав­нения, булева алгебра, графы и т. д.), но все они есть не более чем отношения вида (3.1). В условиях предельно нечеткой инфор­мации, когда систему удается описать лишь качественно, все словесные утверждения в силу их лингвистических функций определяют отношения типа (3.1). Действительно, каждое высказыва­ние содержит две основные лингвистические категории: термы (денотаты) и функторы. Напомним, что термы используются для обозначения объектов, а функторы — для обозначения отноше­ния между ними. И для каждого правильного множества словес­ных утверждений существует отношение (в математическом смы­сле слова), описывающее формальную взаимосвязь между объектами. Таким образом, система всегда является отношением в смысле (3.1), а уже более узкие классы систем определяются более точно своими специфическими средствами.

3. Системы часто задаются с помощью некоторых уравнений относительно соответствующих переменных. Каждой такой пере­менной можно поставить в соответствие некоторый объект систе­мы, описывающей область значений соответствующей перемен­ной. Утверждая, что система описывается системой уравнений относительно некоторого множества переменных, в сущности считают, что система есть отношение над соответствующими объектами, порожденными этими переменными (по одному объекту на каждую переменную, область значений которой он представляет). При этом любая комбинация элементов этих объектов, принадлежащая этому отношению, удовлетворяет ис­ходной системе уравнений.