Лекция 10. Моды оптических резонаторов
Конфокальный резонатор и его свойства. Расчет поля и определение собственных колебаний в резонаторе произвольной конфигурации могут быть выполнены аналогично тому, как это было сделано для резонатора с плоскими зеркалами, поскольку соотношения (6.51) - (6.54) справедливы для общего случая.
В отличие от плоского резонатора, для конфокального резонатора интегральное уравнение (6.53) с ядром (6.54) имеет аналитическое решение. Интерес к конфокальному резонатору обусловлен удобством его юстировки, в отличие от плоскопараллельного резонатора Фабри-Перо не требующей строгой параллельности отражателей друг другу. Конфокальный резонатор может быть образован сферическими или параболическими зеркалами. Мы ограничимся только случаем сферических зеркал.
В резонаторе со сферическими зеркалами существуют те же типы колебаний, что и в плоскопараллельном резонаторе. Однако распределение амплитуды и фазы поля на поверхности его зеркал для одних и тех же типов колебаний отлично от распределения в плоскопараллельном резонаторе. Оказывается, что в конфокальном резонаторе поверхности зеркал являются поверхностями равных фаз, т.е. распределение фазы по поверхности каждого зеркала однородно. Поле в конфокальном резонаторе сильнее сконцентрировано у оси и падает на краях зеркал до гораздо меньшей величины, чем в плоскопараллельном резонаторе. Очень важным обстоятельством является то, что потери мощности в таких резонаторах могут быть на несколько порядков меньше, чем в плоскопараллельном резонаторе.
Рассмотрим конфокальный резонатор более подробно.
1. Пространственное распределение интенсивности мод. Пусть все размеры резонатора велики по сравнению с длиной волны. Тогда моды резонатора, распределение полей в нем и дифракционные потери можно получить на основе принципа Гюйгенса-Френеля путем решения соответствующего интегрального уравнения (6.53) с ядром (6.54). Для сферических зеркал с прямоугольной или круглой апертурой это интегральное уравнение допускает разделение переменных относительно поперечных координат и сводится к одномерным интегральным уравнениям. Если отражатели симметричного конфокального резонатора имеют квадратное сечение со стороной 2а, которая мала по сравнению с расстоянием между зеркалами L, равным их радиусу кривизны R, а числа Френеля велики, то собственные функции интегрального уравнения типа Фокса и Ли аппроксимируются произведениями полиномов Эрмита 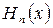 на гауссову функцию
на гауссову функцию 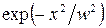 .
.
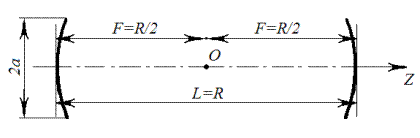 |
 В декартовой системе координат, начало которой помещено в центр резонатора, т. е. в конфокальную точку, а ось z совпадает с осью резонатора (см. рис. 6.13), поперечное распределение поля дается выражением
В декартовой системе координат, начало которой помещено в центр резонатора, т. е. в конфокальную точку, а ось z совпадает с осью резонатора (см. рис. 6.13), поперечное распределение поля дается выражением
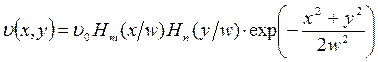 , (6.56)
, (6.56)
где w определяет размер той области поперечного сечения, при выходе из которой интенсивность поля в резонаторе, пропорциональная 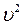 , падает в е раз. Другими словами, величина w является шириной распределения интенсивности. В пятне площадью
, падает в е раз. Другими словами, величина w является шириной распределения интенсивности. В пятне площадью 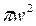 сосредоточена в основном энергия волны, проходящей в направлении z через плоскость ху.
сосредоточена в основном энергия волны, проходящей в направлении z через плоскость ху.
Полиномы Эрмита нескольких первых степеней имеют вид
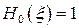 ,
, 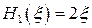 ,
, 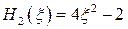 ,
, 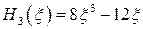 . (6.57)
. (6.57)
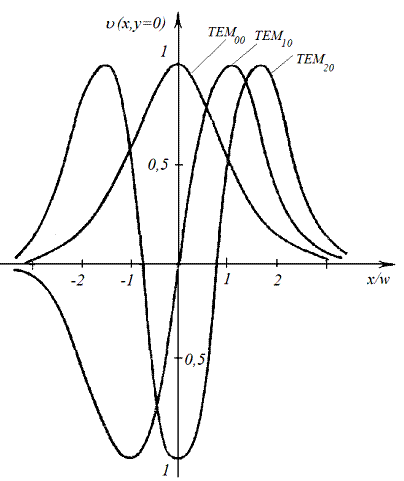
Выражение (6.56) описывает поперечные распределения поля для 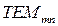 -мод в конфокальном резонаторе. На рис. 6.14 показаны эти распределения для первых трех мод. Эти графики наглядно показывают характер изменения поперечного распределения поля с увеличением поперечного индекса m.
-мод в конфокальном резонаторе. На рис. 6.14 показаны эти распределения для первых трех мод. Эти графики наглядно показывают характер изменения поперечного распределения поля с увеличением поперечного индекса m.
Для основной 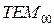 -моды наблюдается гауссово распределение интенсивности
-моды наблюдается гауссово распределение интенсивности
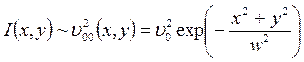 . (6.58)
. (6.58)
Для последующих мод характерно более сложное распределение с симметричным чередованием максимумов и нулевых минимумов. Число минимумов в распределении равно соответствующему индексу моды, а число максимумов – на единицу больше. Периферийные максимумы распределения больше центральных.
Если зеркала конфокального резонатора круглые, то распределение интенсивности в поперечном сечении имеет иной вид:
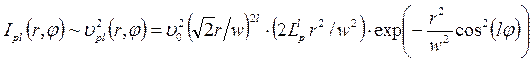 , (6.59)
, (6.59)
где 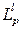 – полиномы Лагерра;
– полиномы Лагерра; 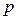 и
и 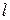 – соответственно радиальный и угловой индексы моды. Для мод низших радиальных порядков полиномы Лагерра равны:
– соответственно радиальный и угловой индексы моды. Для мод низших радиальных порядков полиномы Лагерра равны:
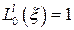 ,
, 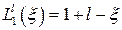 ,
, 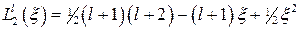 . (6.60)
. (6.60)
 |
 Рассматривая выражение (6.59), нетрудно видеть, что распределение в основной моде при центральной симметрии резонатора также описывается функцией Гаусса и, стало быть, не отличается от случая прямоугольной симметрии. Однако для типов колебаний высших порядков распределение интенсивности имеет более сложный характер с периодическим чередованием экстремумов. Число минимумов при изменении радиальной координаты от
Рассматривая выражение (6.59), нетрудно видеть, что распределение в основной моде при центральной симметрии резонатора также описывается функцией Гаусса и, стало быть, не отличается от случая прямоугольной симметрии. Однако для типов колебаний высших порядков распределение интенсивности имеет более сложный характер с периодическим чередованием экстремумов. Число минимумов при изменении радиальной координаты от 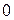 до
до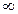 равно
равно 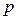 , а число минимумов при изменении угловой координаты от
, а число минимумов при изменении угловой координаты от 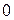 до
до 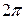 равно
равно 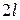 .
. 2. Частотный спектр. Собственным функциям уравнения, дающим поперечное распределение поля для случая сферических зеркал с квадратной апертурой (6.56), соответствуют собственные частоты, определяемые условием:
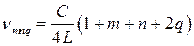 . (6.61)
. (6.61)
Видно, что спектр мод конфокального резонатора вырожден. Действительно, поперечные моды, индексы которых удовлетворяют условию
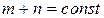 (6.62)
(6.62)
имеют одинаковые частоты, хотя их пространственные конфигурации будут различными. Аналогично, увеличение 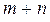 на две единицы и уменьшение q
на две единицы и уменьшение q
на единицу тоже дает одинаковое значение частоты.
Легко заметить также, что взаимное расположение мод конфокального резонатора на шкале частот (т.е. спектр мод) существенно отличается от спектра мод плоскопараллельного резонатора.
Действительно, частотные интервалы между различными модами равны
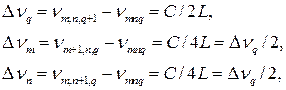 (6.63)
(6.63)
откуда следует, что все невырожденные поперечные моды расположены эквидистантно по спектру, причем расстояние между соседними модами в этом спектре равно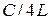 . С другой стороны, в каждой поперечной моде соответствующие ей продольные моды также расположены эквидистантно, но с интервалом в два раза большим, т.е.
. С другой стороны, в каждой поперечной моде соответствующие ей продольные моды также расположены эквидистантно, но с интервалом в два раза большим, т.е. 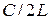 .
.
3. Характеристики гауссова пучка. Симметричный конфокальный резонатор. Как отмечалось выше, в конфокальном резонаторе основной является мода 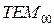 , поперечное распределение интенсивности в которой определяется простой гауссовой функцией
, поперечное распределение интенсивности в которой определяется простой гауссовой функцией 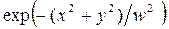 . Ширина распределения интенсивности (ширина пучка) в симметричном конфокальном резонаторе меняется вдоль оси z по закону
. Ширина распределения интенсивности (ширина пучка) в симметричном конфокальном резонаторе меняется вдоль оси z по закону
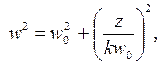 (6.64)
(6.64)
где 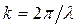 , a w0 имеет смысл радиуса пучка в фокальной плоскости резонатора, т. е. при z = 0, и обычно называется радиусом перетяжки или радиусом шейки каустики. Величина w0 определяется длиной резонатора и составляет
, a w0 имеет смысл радиуса пучка в фокальной плоскости резонатора, т. е. при z = 0, и обычно называется радиусом перетяжки или радиусом шейки каустики. Величина w0 определяется длиной резонатора и составляет
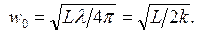 (6.65)
(6.65)
На поверхности зеркала, т. е. при z = L/2, площадь пятна основной моды, как это видно из (6.64) и (6.65), вдвое больше, чем площадь сечения шейки каустики.
Следует пояснить понятие каустики пучка. Поверхность равной относительной интенсивности излучения представляет собой поверхность гиперболоида вращения, ось которого совпадает с осью резонатора. Линии, образующиеся при осевом сечении этой поверхности плоскостью, называются каустикой пучка (рис. 6.15). Она описывается выражением (6.64), которое по сути есть уравнение второго порядка.
Поверхности равных фаз для гауссова пучка представляют собой сферические поверхности. Радиус кривизны синфазной поверхности, пересекающей оптическую ось резонатора в точке z (напомним, что начало отсчета совпадает с общим фокусом зеркал), определяется соотношением
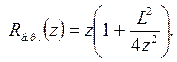 (6.66)
(6.66)
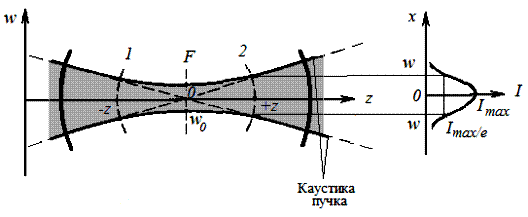 |
 След этой поверхности изображен на рис. 6.15 пунктирными линиями. С приближением к центру резонатора радиусы кривизны синфазных поверхностей увеличиваются. При z = 0
След этой поверхности изображен на рис. 6.15 пунктирными линиями. С приближением к центру резонатора радиусы кривизны синфазных поверхностей увеличиваются. При z = 0 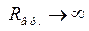 , т. е. синфазная поверхность в плоскости симметрии резонатора является плоской. Это означает, что в фокальной перетяжке волна является плоской, но пространственно ограниченной эффективным размером w0. При
, т. е. синфазная поверхность в плоскости симметрии резонатора является плоской. Это означает, что в фокальной перетяжке волна является плоской, но пространственно ограниченной эффективным размером w0. При 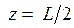 радиус
радиус 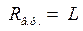 , т.е. на поверхности зеркала волновой фронт совпадает со сферической поверхностью зеркала. На больших расстояниях от начала координат (
, т.е. на поверхности зеркала волновой фронт совпадает со сферической поверхностью зеркала. На больших расстояниях от начала координат ( 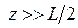 ) радиус кривизны сферического волнового фронта совпадает с расстоянием от резонатора до фронта волны: Rв.ф. ≈ z. Это означает, что в дальней зоне волновой фронт гауссова пучка приближается к волновому фронту сферической волны, распространяющейся из точки, расположенной на оси пучка в месте его фокальной перетяжки. Размер перетяжки w0 определяет расходимость основной моды
) радиус кривизны сферического волнового фронта совпадает с расстоянием от резонатора до фронта волны: Rв.ф. ≈ z. Это означает, что в дальней зоне волновой фронт гауссова пучка приближается к волновому фронту сферической волны, распространяющейся из точки, расположенной на оси пучка в месте его фокальной перетяжки. Размер перетяжки w0 определяет расходимость основной моды 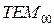 .
. Распределение амплитуды по волновому фронту гауссового пучка (6.58) обладает осевой симметрией и шириной w (6.64). На большом расстоянии от резонатора ( 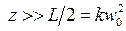 ) ширина
) ширина 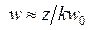 , чему соответствует угловая расходимость
, чему соответствует угловая расходимость
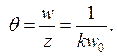 (6.67)
(6.67)
В результате основная часть энергии гауссова пучка сосредоточена в телесном угле
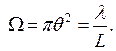 (6.68)
(6.68)
Обратим внимание, что расходимость пучка в основной моде конфокального резонатора определяется не поперечным, а продольным размером L резонатора. Аналогично, поперечный размер w пучка, определяемый выражением (6.64), не зависит от поперечного размера зеркала 2а. Это является следствием сделанных выше предположений о малости значения отношения 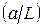 и о большом значении числа Френеля
и о большом значении числа Френеля 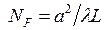 .
.
Решения (6.56) и (6.59) получены для поля внутри резонатора. Но когда одно из зеркал частично прозрачно, как это и бывает в случае активных лазерных резонаторов, то выходящая наружу волна является бегущей волной с тем же поперечным тем же распределением.
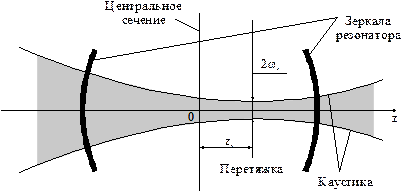
4. Несимметричный конфокальный резонатор. В конфокальном резонаторе с одинаковыми зеркалами положение перетяжки совпадает с центральным сечением резонатора. Если зеркала имеют различную кривизну поверхности, то перетяжка не совпадает с центральном сечением, а отстоит от него на некотором расстоянии, величину которого можно рассчитать по формуле
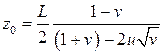 , (6.69)
, (6.69)
где u и ν – параметры конфигурации резонатора:
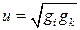 ,
, 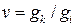 , где
, где 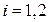 ,
, 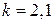 . (6.70)
. (6.70)
В общем случае перетяжка смещена от центрального сечения в сторону зеркала меньшей кривизны. Если одно из зеркал является плоским (полуконфокальный резонатор), то перетяжка совпадает с ним. Для выпукло-вогнутой конфигурации зеркал она располагается вне резонатора.
 |
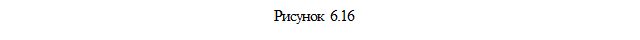
Размер перетяжки определяется параметрами резонатора (6.70) и длиной волны излучения генерации лазера:
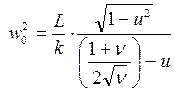 , (6.71)
, (6.71)
где 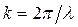 . Размер пятна по обе стороны от перетяжки увеличивается по закону
. Размер пятна по обе стороны от перетяжки увеличивается по закону
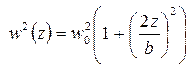 , (6.72)
, (6.72)
где 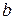 – конфокальный параметр резонатора.
– конфокальный параметр резонатора.
Конфокальный параметр резонатора определяется как высота гиперболоида, поверхность которого образована каустикой пучка, а площадь торцов больше площади сечения перетяжки в два раза. Конфокальный параметр симметричного конфокального резонатора совпадает с его длиной 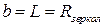 .
.
Интересно то, что на торцах такого гиперболоида сферический волновой фронт пучка имеет максимальную кривизну. При удалении в обе стороны от торцов кривизна уменьшается, и в плоскости перетяжки, а также на бесконечности волновой фронт становится плоским. Изменение радиуса кривизны волнового фронта вдоль оси пучка определяется формулой
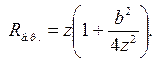 (6.73)
(6.73)
Неустойчивые резонаторы и их особенности. В лазерах повышенной мощности, в частности, в технологических лазерах, в последнее время широкое распространение получили неустойчивые резонаторы со сферическими металлическими зеркалами. Причины, по которым они привлекают к себе столь пристальное внимание, состоят в следующем.
1. Для достижения высоких уровней мощности излучения моды лазерного резонатора должны иметь достаточно большой объем, чтобы снимать инверсию со всего активного элемента лазера. Поскольку в устойчивом резонаторе излучение стремится сосредоточиться вблизи его оси, то поперечное сечение (а значит и объем) его мод мало, в результате чего инверсия снимается лишь с части объема активного элемента. Напротив, в неустойчивом резонаторе излучение стремится покинуть его через боковую поверхность и как бы "размывается" по всей активной среде, снимая инверсию полностью со всего ее объема.
2. Поскольку в неустойчивом резонаторе излучение теряется через его боковую поверхность, то это обстоятельство можно использовать для вывода лазерного пучка. При этом появляется возможность применять вместо обычных полупрозрачных зеркал с диэлектрическим покрытием зеркала из различных металлов, что существенно повышает надежность лазеров и уровень их мощности.
3. Характер связи неустойчивого резонатора со свободным пространством таков, что излучаемый пучок имеет большую апертуру и хорошо коллимируется без применения телескопической оптики.
4. В неустойчивом резонаторе значительно легче осуществить селекцию поперечных мод.
Рассмотрим самый распространенный тип неустойчивого резонатора –телескопический конфокальный резонатор.
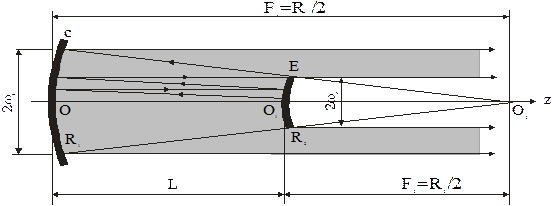
Неустойчивый телескопический конфокальный резонатор. Его схема представлена на рис. 6.17. Он состоит из двух металлических сферических зеркал, одно из которых – вогнутое с радиусом отражающей поверхности 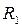 , а второе – с радиусом отражающей поверхности
, а второе – с радиусом отражающей поверхности 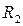 – выпуклое. Конфокальность для такого резонатора имеет место при выполнении условия
– выпуклое. Конфокальность для такого резонатора имеет место при выполнении условия
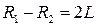 . (6.74)
. (6.74)
В лазере с таким неустойчивым резонатором генерация возникает в приосевой зоне. Многократно отражаясь от зеркал, излучение усиливается и покидает приосевую зону, смещаясь к периферии резонатора. Относительная величина смещения луча на выпуклом зеркале за один проход резонатора называется коэффициентом увеличения резонатора. Из рисунка видно, что треугольники 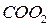 и
и 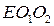 подобны друг другу, поэтому коэффициент увеличения можно представить в виде
подобны друг другу, поэтому коэффициент увеличения можно представить в виде
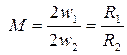 , (6.75)
, (6.75)
где 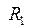 и
и 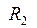 – радиусы зеркал. Нетрудно видеть, что пятно выходного излучения лазера с таким резонатором будет иметь форму кольца.
– радиусы зеркал. Нетрудно видеть, что пятно выходного излучения лазера с таким резонатором будет иметь форму кольца.
В отличие от устойчивого резонатора прозрачность неустойчивого определяется не пропусканием выходного зеркала, а отношением площади кольца выходного излучения к площади сечения, занятого излучением:
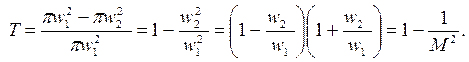 (6.76)
(6.76)
 |
Из-за геометрического расширения излучения в резонаторе его интенсивность падает на одном проходе в
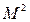 раз. Однако в стационарных условиях генерации и при малых внутрирезонаторных потерях усиление излучения на одном проходе также составляет
раз. Однако в стационарных условиях генерации и при малых внутрирезонаторных потерях усиление излучения на одном проходе также составляет 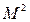 . Таким образом, весь резонатор заполнен излучением с практически равной интенсивностью, что и обеспечивает полное и равномерное использование всей активной среды, и каустика пучка имеет вид прямой линии.
. Таким образом, весь резонатор заполнен излучением с практически равной интенсивностью, что и обеспечивает полное и равномерное использование всей активной среды, и каустика пучка имеет вид прямой линии.  Естественно, неустойчивые резонаторы обладают и рядом недостатков, к которым можно отнести следующее.
Естественно, неустойчивые резонаторы обладают и рядом недостатков, к которым можно отнести следующее.
1. Поперечное сечение пучка, выходящего из резонатора, имеет форму кольца, т.е. в его центре находится темное пятно. Однако этот недостаток для многих приложений легко устраним. Можно показать, что если для фокусировки пучка использовать сферическую линзу, то в ее фокальной плоскости (в дальней волновой зоне) это темное пятно исчезает.
2. Распределение интенсивности в пучке излучения, выходящего, из неустойчивого, резонатора, является неоднородным: оно имеет несколько дифракционных колец.
