Напряжения и перемещения бруса круглого поперечного сечения
Необходимость расчета брусьев при кручении связана с проверкой прочности и жесткости бруса.
Прочность бруса при кручении обеспечивают касательные напряжения 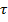 в плоскости поперечного сечения бруса. Эти напряжения приводят к своей равнодействующей – крутящему моменту в сечении
в плоскости поперечного сечения бруса. Эти напряжения приводят к своей равнодействующей – крутящему моменту в сечении 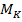 (рис. 6.3, а).
(рис. 6.3, а).
Теория кручения бруса круглой формы основана на таких гипотезах и допущениях:
а) поперечное сечение бруса, плоское и перпендикулярное к его оси до деформации кручения, остается плоским и нормальным к его оси после деформации (гипотеза плоских сечений);
б) радиусы поперечных сечений при деформации не искривляются;
в) материал бруса подчиняется закону Гука между напряжениями и деформациями.
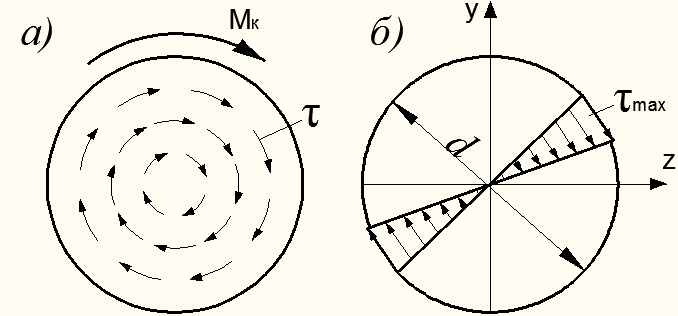
Рисунок 6.3 – Касательные напряжения в сечении бруса
Максимальные касательные напряжения 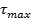 , по которым проверяется прочность при кручении, вычисляются в опасном сечении бруса, где действует наибольший по абсолютной величине крутящий момент
, по которым проверяется прочность при кручении, вычисляются в опасном сечении бруса, где действует наибольший по абсолютной величине крутящий момент 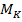 . Касательные напряжения распределяются по сечению по линейному закону; опасной точкой будет наиболее удаленная от центра сечения точка на поверхности бруса (рис. 6.3, б). По этим напряжениям проверяется прочность при кручении бруса. Тогда для бруса (вала) круглого сплошного или кольцевого поперечного сечения:
. Касательные напряжения распределяются по сечению по линейному закону; опасной точкой будет наиболее удаленная от центра сечения точка на поверхности бруса (рис. 6.3, б). По этим напряжениям проверяется прочность при кручении бруса. Тогда для бруса (вала) круглого сплошного или кольцевого поперечного сечения:
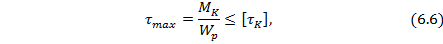
где 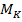 – наибольший крутящий момент в опасном сечении бруса;
– наибольший крутящий момент в опасном сечении бруса; 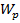 – полярный момент сопротивления сечения:
– полярный момент сопротивления сечения:
· для круглого сплошного сечения
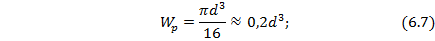
· для кольцевого сечения
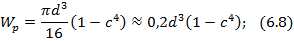
 – диаметр сплошного сечения и внешний диаметр кольцевого сечения;
– диаметр сплошного сечения и внешний диаметр кольцевого сечения; 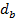 – внутренний диаметр кольца;
– внутренний диаметр кольца; 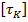 – допускаемое касательное напряжение при кручении, равное для стального материала бруса
– допускаемое касательное напряжение при кручении, равное для стального материала бруса 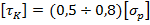 .
.
Из формулы (6.6) можно определить как необходимый диаметр вала 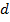 , так и допускаемую нагрузку при кручении
, так и допускаемую нагрузку при кручении 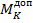 на основании теорий прочности.
на основании теорий прочности.
Угол поворота одного сечения относительно другого называется полным углом закручивания бруса между этими сечениями.
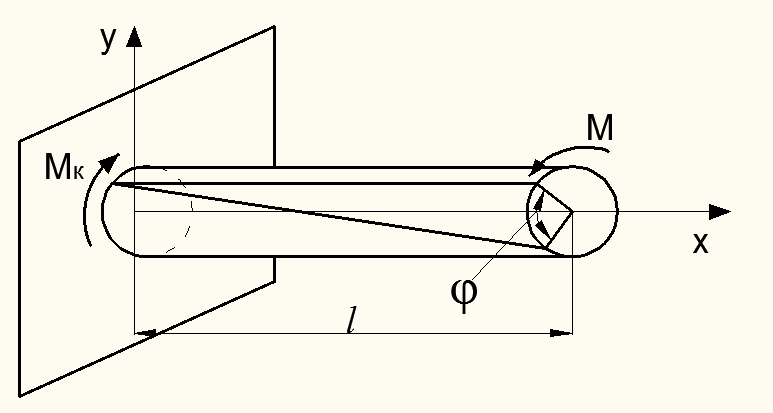
Рисунок 6.4 – Угол закручивания бруса при деформации кручения
Полный угол закручивания бруса длиной 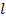 определяется по формуле
определяется по формуле
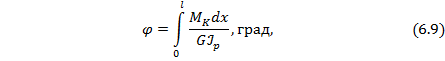
где 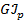 – жесткость сечения при кручении;
– жесткость сечения при кручении; 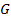 – модуль сдвига;
– модуль сдвига; 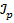 – полярный момент инерции сечения.
– полярный момент инерции сечения.
Для круглого сплошного сечения бруса
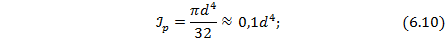
Для кольцевого сечения бруса
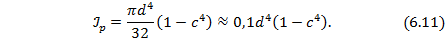
При 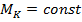 и
и 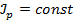 (брус постоянного сечения) полный угол закручивания участка длиной
(брус постоянного сечения) полный угол закручивания участка длиной 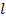 определяется по формуле:
определяется по формуле:
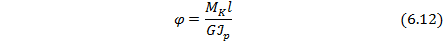
Полный угол закручивания не всегда может характеризовать жесткость вала на кручение. Для этой цели вводится другая величина – относительный угол закручивания 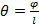 .
.
Условие жесткости при кручении имеет вид:
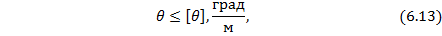
где 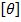 – допускаемый относительный угол закручивания, выбираемый для разных конструкций и видов нагрузок в пределах
– допускаемый относительный угол закручивания, выбираемый для разных конструкций и видов нагрузок в пределах 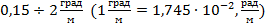 .
.
Из условия жесткости (6.13) можно определить как необходимый диаметр вала 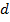 , так и допускаемую нагрузку
, так и допускаемую нагрузку 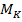 .
.
Если погонный угол закручивания φ по формуле (6.11) имеет размерность 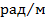 , то крутящий момент
, то крутящий момент 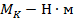 ,
, 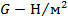 ,
, 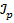 –
– 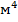 ; при размерности φ в
; при размерности φ в 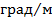 ,
, 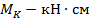 ,
, 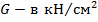 и
и 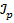 –
– 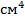 .
.
Формула для угла поворота (6.8) на і-м участке 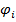 относительно концевого сечения вала имеет вид:
относительно концевого сечения вала имеет вид:
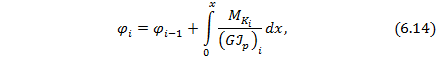
где 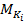 – крутящий момент на -м участке;
– крутящий момент на -м участке; 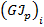 – жесткость
– жесткость 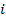 -го участка;
-го участка; 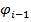 – угол поворота концевого сечения предыдущего
– угол поворота концевого сечения предыдущего 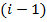 -го участка.
-го участка.
По результатам расчета углов закручивания бруса по формуле (6.13) строится эпюра φ. Положительные ординаты эпюры φ откладываются вверх от горизонтальной линии.
