Статистическое изучение сезонных колебаний

Под сезонными колебаниями понимаются более или менее устойчивые внутригодовые колебания уровней развития социально-экономических явлений.

Сезонная колеблемость (внутригодовая цикличность) показателей рынка выявляется с помощью индексов сезонности, методов механического сглаживания, гармоникой Фурье. Гармоника Фурье имеет следующие аналитическое выражение:

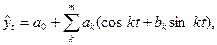
где k – номер гармоники, определяющей степень точности (адекватности) модели (обычно k берётся в пределах от 1 до 4);

t – время;

а₀, а_k, b_k – параметры уравнения.

При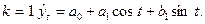

При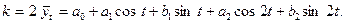

Параметры уравнения ( 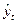) определяются методом наименьших квадратов:

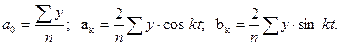
При анализе внутригодовой динамики n = 12 – по числу месяцев в году. Представляя месячные периоды как части окружности, ряд внутригодовой динамики имеет следующий вид:

Периоды, t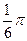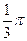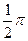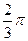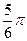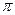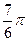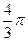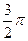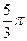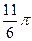

Уровни, y

y1

y2

y3

y4

y5

y6

y7

y8

y9

y10

y11

y12

Для расчёта гармоники используется вспомогательная таблица. Для первой гармоники она имеет следующий вид:

Месяц	Условное обозначение месяца, t	Уровни ряда, y	cos t	sin t	y · cos t	y · sin t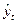
. . и т.д.	1/6 π 1/3 π	y1 y2 y3

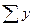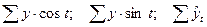Решение типовых задач

Пример 6.1

Розничный товарооборот в регионе в 2008 – 2012 гг. характеризуется

следующими данными, млн руб:

2008 г.	2009 г.	2010 г.	2011 г.	2012 г.
8 900	8 670	8 930	8 990

Для анализа ряда динамики определим:

1) показатели, характеризующие динамику товарооборота по годам;

2) средние показатели динамики за исследуемый период.

Решение

Показатели динамики уровней временного ряда с постоянной (базисные) и переменной (цепные) базой сравнения:

1) абсолютный прирост – ;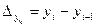

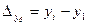
2) коэффициент роста – ;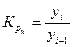

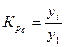
3) темп роста – ;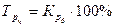

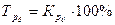
4) темп прироста – ; .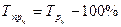

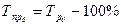5) абсолютное значение 1 % прироста – ;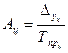

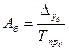
6) пункты роста – .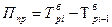

Результаты расчётов приведены в таблице:

Год	2008 г.	2009 г.	2010 г.	2011 г.	2012 г.
Розничный товарооборот, млн руб.
Абсолютный прирост, млн руб.	Цепной	–	–230
Базисный	–	–230
Коэффициент роста	Цепной	–	0,974	1,029	1,006	1,012
Базисный	–	0,974	1,003	1,010	1,022
Темп роста, млн руб.	Цепной	–	97,4	102,9	100,6	101,2
Базисный	–	97,4	100,3	101,0	102,2
Темп прироста, млн руб.	Цепной	–	–2,8	2,9	0,6	1,2
Базисный	–	–2,8	0,3	1,0	2,2
Абсолютное значение 1% прироста, млн руб.	Цепной	–	82,14	89,66	100,00	91,67
Базисный	–	82,14	100,00	90,00	90,91
Пункты роста	–	–	2,9	0,7	1,2

Средние характеристики ряда динамики:

1) средний уровень интервального ряда рассчитывается по формуле средней арифметической простой:

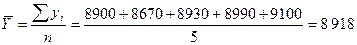млн руб.

2) средний абсолютный прирост ( ):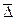

,

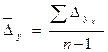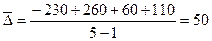млн руб.

3) средний коэффициент роста ( ):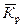

;

;

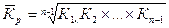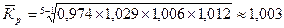4) средний темп роста:

;

;

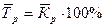
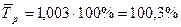5) средний темп прироста:

;

;

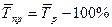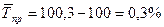6) средняя величина абсолютного значения 1% прироста:

;

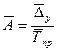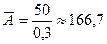млн руб..

Сделаем выводы:

1. Так как темпы роста начиная с 2010 г. имеют значение больше100, то это говорит о тенденции роста объёма розничного товарооборота в регионе.

2. Средний годовой уровень объёма товарооборота в исследуемом периоде составил 8 918 млн руб.

3. В среднем ежегодно товарооборот увеличился на 50 млн руб., или на 0, 3 %

4. Средняя величина абсолютного значения 1% прироста показывает, что при увеличении производства электроэнергии на 1% в абсолютном выражении этот прирост составит 166,7 млн руб.

Пример 6.2

Выполним интервальный прогноз объёма реализации продукции А на 2008 г. с вероятностью 0,99 на основе следующих отчётных данных торгового предприятия:

Год
Объём реализа-ции, т

Для определения формы тренда и расчёта его параметров составим таблицу:

Год	Объём реализации, т y	Первые разности	t	t2	y · t	yt	(y – yt)2
		-	-7		-532	76,53	0,2809
			-5		-435	87,45	0,2025
			-3		-297	98,37	0,3969
			-1		-109	109,25	0,0625
			+1			120,21	0,0441
			+3			131,13	0,7569
			+5			142,05	0,0025
			+7		1 064	52,97	0,9409
Итого		-				917,96	2,6872

Первые разности приблизительно равны между собой, что позволяет в качестве модели тренда выбрать уравнение прямой:

y_t = a₀ + a₁ · t.

Найдем параметры уравнения:

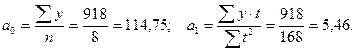
Подставим найденные значения параметров в уравнение:

y_t = 114,75 + 5,46 t.

Рассчитаем теоретические уровни ряда динамики:

2000 г.: y_t = 114,75 + 5,46 · (-7) = 76,53 т.

2001 г.: y_t = 114,75 + 5,46 · (-5) = 87,45 т. и т.д.

Выполним точечный прогноз на 2008 г.:

y_t+L = 114,75 + 5,46 · 9 = 163,89 т.

Для получения интервального прогноза воспользуемся формулой

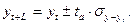
Коэффициент доверия 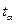находим по таблице распределения Стьюдента (Приложение Б). При вероятности P = 0,99, (уровень значимости α = 1,0), числе степеней свободы k = n – 2 = 6 коэффициент доверия t_α = 3,7.

Рассчитаем стандартную ошибку аппроксимации:

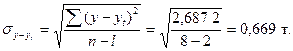
Расчёты квадратов отклонений теоретических уровней ряда от эмпирических приведены в таблице.

Выполним интервальный прогноз

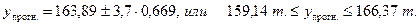
Пример 6.3.Имеются следующие данные о реализации фруктов в магазинах города:

Месяц	Продано фруктов, т	Расчётная графа
Условное обозначение месяца, t	cos t	sin t	y · cos t	y · sin t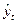
				0,0	68,00		75,03
		1/6 π	0,866	0,5	47,63	27,50	50,11
		1/3 π	0,5	0,866	25,00	43,30	34,86
		1/2 π	0,0	1,0			33,35
		1/3 π	-0,5	0,866	-27,00	46,764	46,00
		5/6 π	-0,866	0,5	-56,29	32,50	69,41
		Π	-1,0	0,0	-90,00		97,31
		7/6 π	-0,866	-0,5	-103,92	-60,00	122,23
		4/3 π	-0,5	-0,866	-72,50	-125,57	137,48
		3/2 π	0,0	-1,0		-130,00	138,99
		5/3 π	0,5	-0,866	60,00	-103,92	126,34
		11/6 π	0,866	-0,5	82,27	-47,50	102,93
Итого	1 034	-	-	-	-66,81	-316,93	1 034,04

Построим модель сезонных колебаний в объёме реализации фруктов, используя первую гармонику ряда Фурье:

Первая гармоника имеет вид:

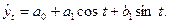
Параметры уравнения определяются по формулам:

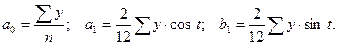
Для определения параметров уравнения введём в таблицу расчётные графы.

Рассчитаем параметры уравнения:

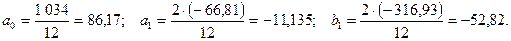
Модель сезонной волны объёма реализации фруктов примет вид:

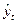= 86,17 – 11,14 cos t – 52,82 sin t.

Определим расчётные (теоретические) уровни для каждого месяца:

январь: 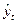= 86,17 – 11,14 · 1,0 – 52,82 · 0 = 75,03 т.

февраль: 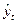= 86,17 – 11,14 · 0,866 – 52,82 · 0,5 = 50,11 т. и т.д.

Результаты 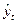расчётов занесём в таблицу.