Булевы функции для описания систем голосования

В этом разделе будет описано использование булевых функций для формализации различ-ных правил голосования в небольших группах (совет директоров, правление банка и пр.). При-ведём пример рассматриваемой ситуации и возникающей в ней формальной задачи.

Пример 19. Комитет состоит из четырёх членов и председателя. Решения принимаются большинством голосов, однако, если председатель голосует «против», то решение не принима-ется. Требуется построить булеву функцию, зависящую от 5 переменных: x₁, x₂, x₃, x₄, y (x_i = 1 тогда и только тогда, когда i-ый член комитета голосует «за» (i = 1, 2, 3, 4), y = 1 тогда и только тогда, когда председатель голосует «за»). Предполагается, что значение этой булевой функции на некотором наборе x₁, x₂, x₃, x₄, y равно 1 тогда и только тогда, когда в результате голосова-ния, соответствующего этому набору, решение принимается. Можно считать, что такая функ-ция (если она существует) описывает данную схему голосования. Её можно назвать функцией голосования ■

Из самой постановки вопроса ясно, что искомая функция является неубывающей (говорят также, монотонно неубывающей). Действительно, пусть при некотором наборе голосов x₁, x₂, x₃, x₄, y решение принимается, т.е. f(x₁, x₂, x₃, x₄, y) = 1. Если бы кто-то из тех, кто голосовал «против», проголосовал «за», решение тем более должно быть принято. Формально неубываю-щая функция f(z₁, …, z_n) характеризуется условием:

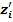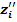≤ (i = 1, 2, …, n)→ f( 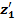, …, 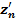) ≤ f( 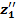, …, 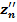). (29)

Будем искать функцию голосования в виде реализующей её ДНФ, в которую все перемен-ные входят без отрицания. Существование такой ДНФ для произвольной неубывающей булевой функции является хорошо известным фактом, который здесь не доказывается.

Алгоритм построения функции голосования.

1. Составить таблицу типа таблицы 1 с заданным числом переменных (т.е. участников го-лосования). В самом левом столбце для удобства записываются числа, двоичным разложением которых служит набор нулей и единиц в данной строке. Для каждого набора значений перемен-ных в правый столбец записать 1, если по исходному словесному описанию схемы голосования, при голосовании участников, соответствующем данному набору, решение принимается. В про-тивном случае записать туда 0. Разумеется, выполнение этого шага требует содержательного анализа рассматриваемой схемы голосования, т.е. шаг не является чисто формальным.

2. Удалить из таблицы все строчки, в правой части которых записан ноль, а из оставшейся таблицы удалить правый столбец, содержащий (после удаления строк) одни единицы. В резуль-тате выполнения этого шага останутся строчки, соответствующие голосованиям, при которых решения принимаются.

3. Самый сложный шаг. Просматривая последовательно все строки таблицы, удаляем i-ую строку, если для неё существует другая строка (среди ещё не удалённых), которая содержит единицы только на тех местах, на которых есть единицы и в i-ой строке. В результате остаются все минимальные голосования, при которых решения принимаются. Минимальность означает, что при изменении позиции любого одного участника с «за» на «против» решение не будет при-нято.

4. Каждой оставшейся строке соответствует конъюнкция, содержащая те и только те пере-менные (без отрицаний), номера которых совпадают с номерами позиций, на которых в данной строке стоят единицы. Например, строке 01101 соответствует конъюнкция x₂x₃y (если послед-няя переменная y сопоставлена председателю).

5. Образуем дизъюнкцию всех полученных на предыдущем шаге конъюнкций. Получен-ная формула реализует искомую функцию голосования ■

Пример 20.Применим алгоритм для схемы голосования, описанной в примере 19. Соста-вим таблицу 13 в соответствии с шагом 1 алгоритма. Сначала часть таблицы, состоящая из столбцов с заголовками x₁, x₂, x₃, x₄, y заполняется в лексикографическом порядке (см. формулу (1)). Затем делается самое главное – заполняется столбец со значениями функции голосования f. По условию, если председатель против, то решение не принимается. Поэтому во всех строках, где y = 0, в столбец f записываем 0, независимо от значений всех других переменных. Поэтому 0 бу-дет в столбце f во всех строках с чётными номерами. В остальных строках, в которых y = 1, ис-пользуется правило большинства, т.е. 1 записывается в последнюю позицию во всех строках, в которых число единиц больше числа нулей, т.е. рано 3, 4 или 5 (а не 2, 1 или 0).

Шаг 2. Для большей ясности сначала подсветим удаляемые строки и столбец (см таблицу 14). После их удаления оставшиеся строки и столбцы образуют таблицу 15.

Шаг 3. Понятно, что строчки, в которых есть ровно три единицы, не могут быть удалены (в данной схеме с учётом правила большинства не может быть строк, в которых меньше трёх единиц). Строка 15 должна быть удалена, поскольку все единицы строки 13 находятся на тех местах, где есть единицы в строке 15. Строка 23 должна быть удалена, поскольку все единицы строки 21 находятся на тех местах, где есть единицы в строке 23. Строка 27 должна быть уда-лена по той же причине из-за строки 25. Строка 29 должна быть удалена по той же причине из-за строки 25. Строка 31 содержит 1 на всех позициях и, конечно, также должна быть удалена. Оставшиеся 6 строк образуют таблицу 16.

Шаг 4. В соответствии с алгоритмом по строчкам таблицы 16 образуем следующие 6 конъюнкций: x₃x₄y, x₂x₄y, x₂x₃y, x₁x₄y, x₁x₃y, x₁x₂y.

Шаг 5. В соответствии с алгоритмом образуем дизъюнкцию всех полученных на предыду-щем шаге конъюнкций. Функция f(x₁, x₂, x₃, x₄, y) = x₃x₄y Ú x₂x₄y Ú x₂x₃y Ú x₁x₄y Ú x₁x₃y Ú x₁x₂y и является в данном случае искомой функцией голосования ■

Таблица 13. Исходные данные для схемы голосования N x1 x2 x3 x4 y

N x1 x2 x3 x4 y

Таблица 14. Удаляемые строки и столбец N x1 x2 x3 x4 y

N x1 x2 x3 x4 y

Таблица 15. Все голосования, при которых принимаются решения N x1 x2 x3 x4 y

Таблица 16. Минимальные голосования, при которых принимаются решения N x1 x2 x3 x4 y

Пример 21.В правление банка входят четыре человека: председатель А, имеющий два го-лоса в своём распоряжении, и члены правления B, C и D, обладающие одним голосом каждый. Для принятия какого-либо решения при голосовании должно быть набрано хотя бы четыре го-лоса. Найдём функцию голосования для описанной схемы.

Сопоставим членам правления B, C и D переменные x₁, x₂ иx₃, председателю А – перемен-ную y. В соответствии с описанной схемой голосования на шаге 1 заполняем таблицу 17:

Таблица 17. Исходные данные для схемы голосования N x1 x2 x3 y

N x1 x2 x3 y

Легко видеть, что без участия председателя остальные участники могут набрать не более 3-ёх голосов, поэтому во всех строчках, где председатель «против», решение не будет принято. В то же время мнения одного председателя не достаточно для принятия решения (нужно ведь 4 голоса «за», а у него только два). Такие же очевидные соображения позволяют легко заполнить эту таблицу.

Далее в соответствии с алгоритмом построения функции голосования выполняем шаг 2, оставляя строчки, соответствующие принятию решения (см. таблицы 18 и 19).

Таблица 18. Удаляемые строки и столбец N x1 x2 x3 y	N x1 x2 x3 y
	Таблица 19. Все голосования, при которых принимаются решения N x1 x2 x3 y	Таблица 20. Минимальные голосования, при которых принимаются решения N x1 x2 x3 y

В результате шага 3 получается таблица 20 минимальных голосований, поскольку лишь набор из строки 15, содержащий только единицы, не является минимальным. Объединяя прос-тые шаги 4 и 5, запишем ответ: функция голосования f(x₁, x₂, x₃, y) = x₂x₃y Ú x₁x₃y Ú x₁x₂y ■

Код Хэмминга

В настоящем разделе рассматривается важное приложение булевых функций – помехоус-тойчивое кодирование. Его суть такова. Имеется двоичный вектор α = (α₁, …, α_d) некоторой фиксированной длины d, который необходимо передать (например, из узла А в узел В телеком-муникационный сети). Известно, что при передаче двоичного вектора возможно не более одной ошибки (т.е. символ 0 может быть воспринят после передачи как 1 или 1 как 0). Требуется раз-работать схему кодирования и декодирования, т.е. предложить:

1. Построение по двоичному вектору α = (α₁, …, α_d) его двоичного кода β = (β₁, …, β_n).

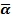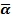2. Построение по полученному при передаче вектора β = (β₁, …, β_n) вектору = ( ₁, …, _n) нового вектора = ( ₁, …, 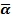_d), такого, что 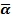= α, независимо от одной ошибки при передаче вектора β.

Данная задача имеет много решений. Например, каждый символ α_i при передаче можно за-

менить тремя совпадающими символами, а при декодировании принимать решение по правилу большинства: если большинство из трёх переданных символов – 0, то α_i = 0, в противном случае α_i = 1. Недостатком такого рода мажоритарных схем является сильное увеличение длины кодов β (в упомянутом случае в три раза). Поэтому требуется, чтобы отношение длины кода n к длине исходного слова d было бы как можно меньше. В частности, очень желательно, чтобы с ростом d указанное отношение стремилось бы к 1. Требуемыми свойствами обладает код Хэмминга, к описанию которого сейчас и переходим.

5.1. Понятия и обозначения. Введём необходимые понятия, обозначения и утверждения, относящиеся к двоичным векторам. Рассмотрим все двоичные векторы длины k. Расположим их в лексикографическом порядке, т.е. в порядке возрастания целых чисел, двоичными разложени-ями которых являются эти векторы:

000…00

000…01

000…10 (30)

………..

111…10

111…11

(см. также формулу (1)). Вектор, стоящий на i-ом сверху месте (начиная с 0) в множестве векто-ров (16), является двоичным разложением числа i. Обозначим его через e^k(i) (0 ≤ i≤ 2^k – 1). На-пример, при k = 3 получаем

e³(0) = 000, e³(1) = 001, e³(2) = 010, e³(3) = 011, e³(4) = 100, e³(5) = 101, e³(6) = 110, e³(7) = 111 (31a)

при k = 4 получаем

e⁴(0) = 0000, e⁴(1) = 0001, e⁴(2) = 0010, e⁴(3) = 0011, e⁴(4) = 0100, e⁴(5) =0101, e⁴(6) = 0110, e⁴(7) = 0111,

e⁴(8) = 1000, e⁴(9) = 1001, e⁴(10) = 1010, e⁴(11) = 1011, e⁴(12) = 1100, e⁴(13) =1101, e⁴(14) = 1110, e⁴(15) = 1111. (31b)

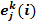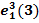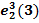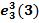Обозначим j-ую координату вектора e^k(i) через (j = 1, …, k). Здесь координаты считаются, как обычно, слева направо. Например,e³(3) = 011, откуда = 0, = = 1.

Особую роль в построении кода Хэмминга играют векторы e^k(i) для i = 2^m (m= 0, 1, …, k – 1). Их координаты обладают тремя почти очевидными свойствами

1. Для любого m = 0, 1, …, k – 1 координата 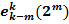= 1,

2. Для любого p < 2^m координата 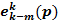= 0.

3. Для любого q > m координата 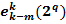= 0.

Все три свойства непосредственно следуют из того, что двоичным разложением длины k числа 2^m является вектор 0…010…0, содержащий только одну единицу на (k–m)-ом месте. Дей-ствительно, так как 1 = 2⁰, то m = 0, k–m = k и в векторе e^k(1) = 00…01 единица действительно стоит на последнем, т.е. k-ом, месте. Далее, так как 2 = 2¹, то m = 1, k–m = k–1, и в векторе e^k(2) = 00…10 единица действительно стоит на предпоследнем, т.е. (k–1)-ом, месте. Аналогично, e^k(4) = 00…100, и т.д.

Пусть β = (β₁, …, β_n) – двоичный вектор длины n. Определим вектор h(β) формулой

h(β) = 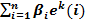, (32)

где число k является минимальным числом, удовлетворяющим неравенству

n < 2^k. (33)

По построению, вектор h(β) имеет k координат. Он получается сложением векторов вида e^k(i), умноженных на 0 или 1. В настоящем разделе под сложением понимается сложение по модулю 2: 0Å0 = 1Å1 = 0, 0Å1 = 1Å0 = 1. При покоординатной записи (32) имеет вид

h_j(β) = 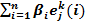(j = 1, …, k). (34)

Обратим внимание, что в (32) и (34) суммирование начинается с 1, а не с 0, поскольку добавле-ние вектора e^k(0), состоящего из одних нулей, не изменит сумм (32) и (34) при любом β₀. Из за-кона 3) дистрибутивности для функции Å (см. раздел 2) и формулы (32) непосредственно сле-дует, что для любых двух двоичных векторов β¹ и β²

h(β¹ Å β²) = h(β¹) Å h(β²). (35)

5.2. Схема кодирования и декодирования. Прежде всего по заданной длине d исходных слов α = (α₁, …, α_d) определим число k как минимальное число, для которого d + k < 2^k. Поло-жим n = d + k. Так как n < 2^k, то любое число от 1 до d + k имеет двоичное разложение длины k (см. векторы (30) и (31)). В таблицу 21 вписаны значения k и n для нескольких небольших d. Из таблицы ясен характер отношения d ⁄n: с ростом d оно стремится к 1.

5.2.1. Кодирование. Определим кодовый вектор β = (β₁, …, β_n) по исходному слову α = (α₁, …, α_d) следующим образом. Занумеруем в порядке возрастания все координаты вектора β,

Таблица 15. Параметры кодирования

d	k	n=d+k	2k

номера которых не являются степенями двойки: β₃, β₅, β₆, β₇, β₉, … . По конструкции, число таких координат в точности равно числу d. Далее, положим

β₃ = α₁, β₅ = α₂, β₆ = α₃, (36)

и т.д. В результате все координаты, номера которых не являются степенями двойки, оказывают-ся «заполненными» координатами исходного вектора α. Указанные координаты вектора β назы-ваются информационными (или информационными разрядами), как раз потому, что они со-держат подлежащую передаче информацию. Остальные разряды, номера которых равны степе-ням двойки: 1, 2, 4, …, называются контрольными.

Пример 22. Рассмотрим исходный набор α = (α₁, α₂, α₃, α₄) длины 4 (d = 4). Прежде всего определим число k из условия d + k < 2^k. Имеем 4 + 2 > 2², 4 + 3 < 2³. Поэтому k = 3, n = d + k = 7 (см. таблицу 21). В векторе β = (β₁, β₂, β₃, β₄, β₅, β₆, β₇) координаты 3, 5, 6 и 7 являются информа-ционными. После присвоения им значений α₁, α₂, α₃, α₄) получаем β = (β₁, β₂, α₁, β₄, α₂, α₃, α₄) ■

Определим теперь контрольные разряды β₁, β₂, β₄, … формулой:

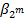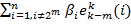= (m = 1, …, k). (37)

В силу указанных выше свойств векторов e^k(i) для i = 2^m в сумму (37) входят только те слагае-мые β_i, для которых

1) номер i >2^m (все мéньшие координаты равны 0 по свойству 2);

2) номер i ≠ 2^q для всех q > m (см. свойство 3).

Учитывая, что информационные разряды β_i – это как раз те, для которых i ≠ 2^q для любых q, формула (37) выражает контрольные разряды только через информационные. Другими словами, формулы (36) и (37) вместе полностью определяют кодирование, поскольку выражают кодовый вектор β = (β₁, β₂,…, β_n) через исходный вектор α = (α₁, …, α_d). Таким образом, алгоритм коди-рования состоит всего из двух шагов.

1. По исходному слову α определяются информационные разряды вектора β по формуле (36).

2. По информационным разрядам вектора β определяются его контрольные разряды по формуле (37).

Пример 23. Построим в явном виде кодовый вектор β = (β₁, β₂, β₃, β₄, β₅, β₆, β₇) по заданно-му вектору α = (α₁, α₂, α₃, α₄) длины 4. Поскольку при d = 4 число k = 3 (см. пример 21), то мож-но записать в явном виде (см. формулы (37)):

β₁ = β₃ Å β₅Å β₇;

β₂ = β₃ Å β₆Å β₇;

β₄ = β₅ Å β₆Å β₇.

Поскольку в данном случае по построению β₃ = α₁, β₅ = α₂, β₆ = α₃, β₇ = α₄, то вместе с предыду-щими равенствами получаем, что все координаты вектора β = (β₁, β₂, β₃, β₄, β₅, β₆, β₇) выражают-ся (притом достаточно просто) через координаты α = (α₁, α₂, α₃, α₄) ■

Нетрудно понять и общую закономерность. При произвольном d и соответствующим ему k (напомним, что k – минимальное число, удовлетворяющее неравенству d + k < 2^k) точно также получим

β₁ = β₃ Å β₅Å β₇ Å … и далее через 1 вплоть до n = d + k,

β₂ = β₃ Å β₆Å β₇ Å β₁₀Å β₁₁ Å … и далее через 2 вплоть до n = d + k,

β₄ = β₅ Å β₆Å β₇ Å β₁₂Å β₁₃ Å β₁₄Å β₁₅ Å … и далее через 4 вплоть до n = d + k, (38)

.……………………………………………………………………………………..

.……………………………………………………………………………………..

Для кода Хемминга имеет место следующее

Утверждение 5. Для кодового вектора β = (β₁, …, β_n), в котором информационные разря-ды заполнены произвольно, а контрольные выражаются через них по формулам (37), верно век-торное равенство

h(β) = 0, (39)

где h(β) определяется формулой (32)

Действительно, если к обеим частям равенства (37) прибавить его левую часть 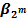, справа получится сумма (32), а слева 0, в силу очевидного тождества АÅА = 0 при любом А ■

Пример 24. Продолжение примера 23. Положим α = 1011. Определим кодовый вектор β формулами из примера 11:

β₁ = β₃ Å β₅Å β₇ = 1 Å 0 Å 1 = 0;

β₂ = β₃ Å β₆Å β₇ = 1 Å 1 Å 1 = 1;

β₄ = β₅ Å β₆Å β₇ = 0 Å 1 Å 1 = 0.

Таким образом, β = 0110011. Имеем (см. 18) и (17а))

h(β) = 0×001Å1×010Å1×011Å0×100Å0×101Å1×110Å1×111=010Å011Å110Å111 = 000 = 0, (40)

в соответствии с утверждением 5.

5.2.2. Декодирование. Передаётся кодовый вектор β = (β₁, …, β_n), определяемый по вход-ному слову α = (α₁, …, α_d) формулами (36) для информационных разрядов и (37) для контроль-ных разрядов. В результате получен вектор = ( ₁, …, _n), отличающийся от β не более, чем в одном разряде. В основе декодирования, т.е. построения по вектору переданного вектора β, лежит следующее

Утверждение 6. Если вектор h( ) = 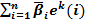(см. формулу (32)) не равен 0, то он явля-ется двоичным разложением числа, равного номеру той единственной координаты вектора = ( ₁, …, _n), которая была искажена при передаче кодового вектора β = (β₁, …, β_n). Если же h( ) = 0,тоошибки при передаче не произошло, т.е. = β.

Доказательство. Предположим, что при передаче вектора β = (β₁, …, β_n) получен вектор = ( ₁, …, _n), и при этом произошло искажение в одном разряде: вместо числа β_s было передано ошибочное число β_s Å 1 (0 вместо 1 или 1 вместо 0). Определим вектор δ, все координаты которого, кроме s-ой, равны 0, а s-ая координата δ_s = 1. Тогда = β + δ. В силу линейности функции h и равенства (39) имеем h( ) = h(β) Å h(δ) = h(δ) = e^k(s). По построению, вектор e^k(s) представ-ляет собой двоичное разложение числа s длины k, что и доказывает утверждение в случае h( ) ≠ 0. В случае h( ) = 0имеем = β, поскольку они могут отличаться только в одном разряде,что и доказывает утверждение в случае h( ) = 0 ■

Доказательство утверждения 6 фактически содержит в себе

Алгоритм декодирования кодов Хэмминга.

1. По вектору = ( ₁, …, _n) и формуле (32) определяем вектор h( ).

2. Если h( ) = 0,то переходим к шагу 4; в противном случае – к шагу 3.

3. По вектору e^k(s) = h( ) ≠ 0 определяем число s, двоичным разложением которого явля-ется e^k(s), и изменяем s-ую координату вектора на противоположное значение.

4. Вектор совпадает с передающимся вектором β. Поэтому компоненты β, находящиеся на местах 1, 3, 5, 6, и т.д., не являющимися степенями 2, как раз и образуют исходное слово α = (α₁, …, α_d) ■

Пример 25. Продолжение примера 24. При передаче кода β = 0110011 произошёл сбой в 3-ьем разряде, т.е. оказался получен вектор = 0100011 вместо β = 0110011. В соответствии с алгоритмом декодирования прежде всего подсчитаем вектор h( ). Имеем (см. для сравнения формулу (40)):

h( ) = 0×001Å1×010Å0×011Å0×100Å0×101Å1×110Å1×111 = 010Å110Å111 = 011 = 3,

что и означает – в силу утверждения 6 – что ошибка действительна произошла в 3-ем разряде. Заменяя 0 в 3-ьем разряде на 1, получаем из ошибочного кода = 0100011 правильный код β = 0110011 ■

Пример 26. Пусть получен вектор = 01001001. Так как его длина n = 9, то из таблицы 15 видно, что k = 4 и длина d исходного сообщения равна 5. Воспользуемся алгоритмом декодиро-вания. Получаем (см. (17b) для векторов e⁴(i)):

h( ) = 0010 Å 0101 Å 1001 = 1110 = 14

(в сумму вошли те слагаемые, которые соответствуют координатам , равным 1). Это означает,

что сбой произошёл в 14-ом разряде. Но 14-го разряда в данном случае просто нет – вектор содержит только 9 координат. В чём же ошибка?

Никакой ошибки нет. Алгоритм декодирования относится только к двоичным векторам, полученных при кодировании методом Хэмминга, или отличающимся от них только в одном разряде. Это означает, что данный вектор 01001001 таковым не является. Если взять все вектора α длины 4, закодировать их описанным в разделе 4.2.1 методом и затем ещё менять все полу-чившиеся векторы ровно в одном разряде, мы никогда не получим данного вектора ■

Задания