Решение тригонометрических уравнений с помощью оценки левой и правой частей уравнения (метод оценок).
Методы решения
Тригонометрических уравнений.
Решение простейших тригонометрических уравнений.
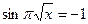
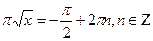
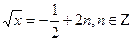
По определению арифметического квадратного корня перейдем к равносильной системе уравнений.
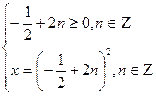
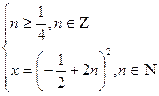
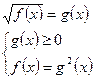
Ответ: 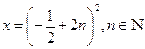
Решение тригонометрических уравнений разложением на множители.
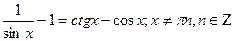
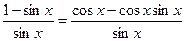
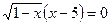
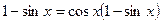
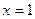 или
или 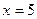
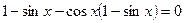
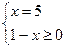
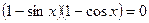
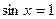 или
или 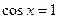 решений нет
решений нет
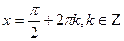
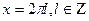
Отметим полученные решения и область определения на тригонометрическом круге.
 |
Решением уравнения является:

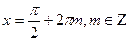
Ответ: 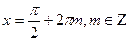
Решение тригонометрических уравнений сводящихся к квадратным уравнениям.
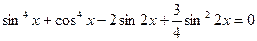
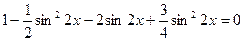
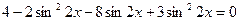
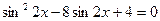
Пусть 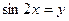 , тогда
, тогда 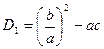
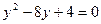
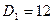
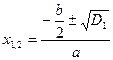
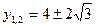
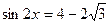 или
или 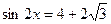
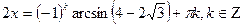 Т.к.
Т.к. 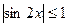
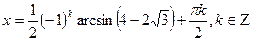 при
при 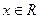 , то корней нет.
, то корней нет.
Ответ: 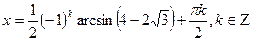
Решение тригонометрических уравнений преобразованием суммы тригонометрических функций в произведение.
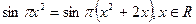
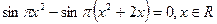
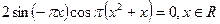
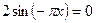 или
или 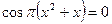
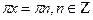
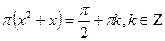
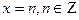
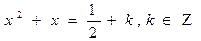
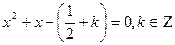
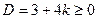
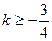
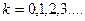
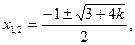
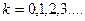
Ответ: 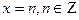 ;
; 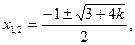
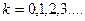
Решение тригонометрических уравнений преобразованием произведения тригонометрических функций в сумму.
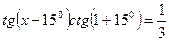
а) Найдем область определения функции.


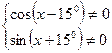

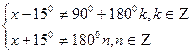
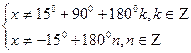
Областью определения данного уравнения является:
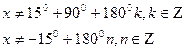
б) Решим данное уравнение.
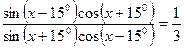
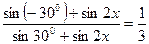
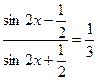
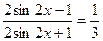
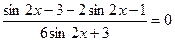
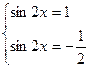


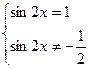

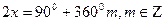
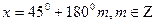
Ответ: 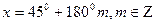
Решение тригонометрических уравнений с применением формул понижения степени.
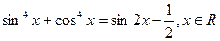
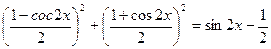
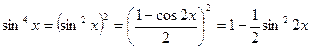
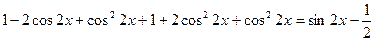
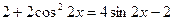
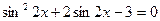
Пусть 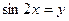 , тогда
, тогда
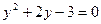
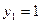
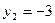
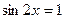 или
или 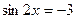
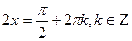 Т.к.
Т.к. 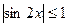
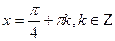 при
при 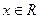 , то корней нет.
, то корней нет.
Ответ: 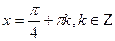
Решение тригонометрических уравнений как однородное.
Однородное уравнение – это уравнение, в котором каждое слагаемое имеет одну и туже степень.
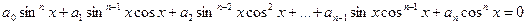 , где
, где
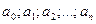 - действительные числа.
- действительные числа. 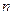 - показатель однородности.
- показатель однородности.
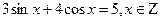
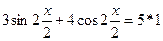
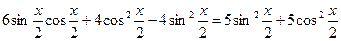
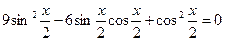
Если 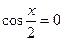 , то и
, то и 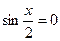 , что противоречит основному тригонометрическому тождеству, значит
, что противоречит основному тригонометрическому тождеству, значит 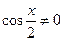 . Разделим обе части на
. Разделим обе части на 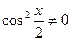 , получим
, получим
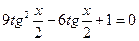
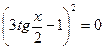
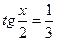
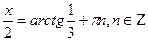
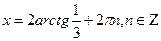
Ответ: 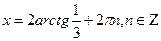
Решение тригонометрических уравнений с помощью введения вспомогательного аргумента.
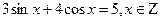
Т. к. 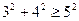 , то корни есть.
, то корни есть.
Разделим обе части уравнения на 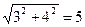 , получим
, получим
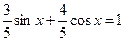
Т. к. 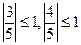 и
и 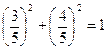 , то существует такой угол
, то существует такой угол 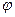 , что
, что 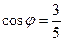 , а
, а 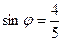 , тогда получим
, тогда получим
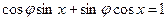
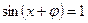
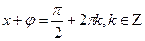
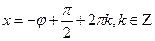
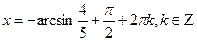 Ответ:
Ответ: 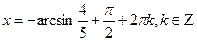
Теория.
1) если 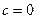 , то уравнение однородное.
, то уравнение однородное.
2) если 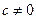 и
и 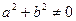 (то есть хотя бы одно из чисел
(то есть хотя бы одно из чисел 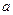 или
или 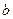 не равно 0), то разделим обе части уравнения на
не равно 0), то разделим обе части уравнения на 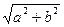 , получим
, получим
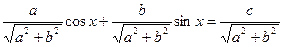
Т. к. 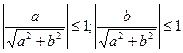 и
и 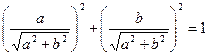 , то существует такой угол
, то существует такой угол  , что
, что 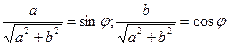 , тогда
, тогда
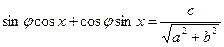
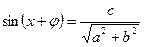
а) если, 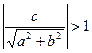 т. е.
т. е. 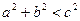 , то корней нет.
, то корней нет.
в) если, 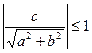 т. е.
т. е. 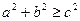 , тогда
, тогда
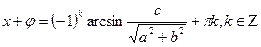
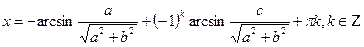
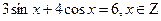
Т. к. 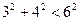 , то корней нет.
, то корней нет.
Решение тригонометрических уравнений с помощью универсальной тригонометрической подстановки.
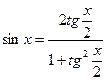
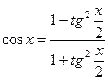
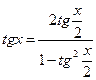
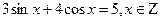 (1)
(1)
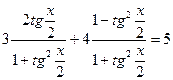 (2)
(2)
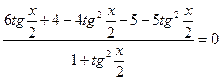
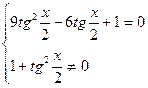
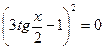
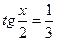
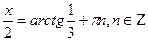
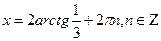
При переходе от уравнения (1) к уравнению (2), могла произойти потеря корней, значит необходимо проверить, являются ли корни уравнения 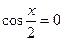 корнями данного уравнения.
корнями данного уравнения.
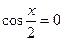
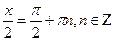
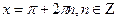
Проверка.
Если 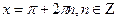 , тогда
, тогда
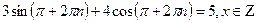
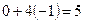 - не верно, значит
- не верно, значит 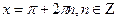 , не является корнями исходного уравнения.
, не является корнями исходного уравнения.
Ответ: 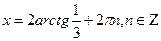
Решение тригонометрических уравнений с помощью замены неизвестного.
Уравнение вида 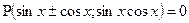 решается следующей заменой
решается следующей заменой 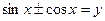 ,
, 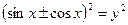 ,
, 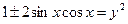 ,
, 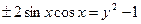
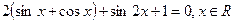
Способ I
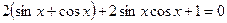
Пусть 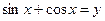 ,
, 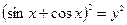 ,
, 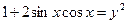 ,
, 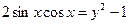 , получим
, получим
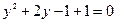
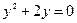
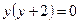
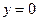 или
или 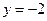
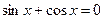
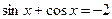 (3)
(3)
Разделим на 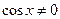 , получим
, получим 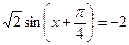
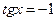
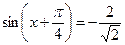
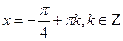 Т. к.
Т. к. 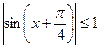 , при
, при 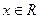 , то корней нет.
, то корней нет.
Ответ: 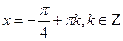
Теория.
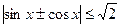 , при
, при 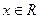
Доказательство:
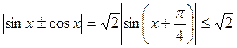
Шесть способов решения уравнения (3).
1. применение формулы 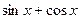 .
.
2. через 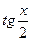 .
.
3. привести к однородному уравнению второй степени.
4. способ введения вспомогательного аргумента.
5. с помощью неравенства 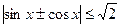 , при
, при 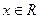 .
.
6. метод оценки левой и правой частей уравнения.
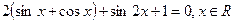
Способ II
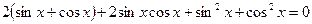
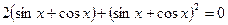
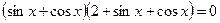
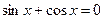 или
или 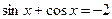
Разделим на 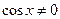 , получим
, получим 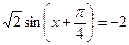
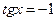
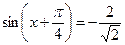
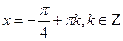 Т. к.
Т. к. 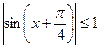 , при
, при 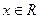 , то корней нет.
, то корней нет.
Ответ: 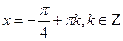
Решение тригонометрических уравнений с помощью оценки левой и правой частей уравнения (метод оценок).
