Проверка общего качества уравнения множественной регрессии
Проверка статистической значимости коэффициентов уравнения множественной регрессии
Как и в случае множественной регрессии, статистическая значимость коэффициентов множественной регрессии с m объясняющими переменными проверяется на основе t-статистики:
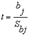
имеющей в данном случае распределение Стьюдента с числом степеней свободы v = n- m-1. При требуемом уровне значимости наблюдаемое значение t-статистики сравнивается с критической точной 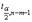 распределения Стьюдента.
распределения Стьюдента.
В случае, если 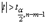 , то статистическая значимость соответствующего коэффициента множественной регрессии подтверждается. Это означает, что фактор Xj линейно связан с зависимой переменной Y. Если же установлен факт незначимости коэффициента bj, то рекомендуется исключить из уравнения переменную Xj. Это не приведет к существенной потере качества модели, но сделает ее более конкретной.
, то статистическая значимость соответствующего коэффициента множественной регрессии подтверждается. Это означает, что фактор Xj линейно связан с зависимой переменной Y. Если же установлен факт незначимости коэффициента bj, то рекомендуется исключить из уравнения переменную Xj. Это не приведет к существенной потере качества модели, но сделает ее более конкретной.
29.Прогнозирование с помощью модели множественной регрессии.
Уравнение регрессии применяют для расчета значений показателя в заданном диапазоне изменения параметров. Оно ограниченно пригодно для расчета вне этого диапазона, т.е. его можно применять для решения задач интерполяции и в ограниченной степени для экстраполяции.
Прогноз, полученный подстановкой в уравнение регрессии ожидаемого значения параметра, является точечным. Вероятность реализации такого прогноза ничтожна мала. Целесообразно определить доверительный интервал прогноза.
Для того чтобы определить область возможных значений результативного показателя, при рассчитанных значениях факторов следует учитывать два возможных источника ошибок: рассеивание наблюдений относительно линии регрессии и ошибки, обусловленные математическим аппаратом построения самой линии регрессии. Ошибки первого рода измеряются с помощью характеристик точности, в частности, величиной 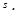 . Ошибки второго рода обусловлены фиксацией численного значения коэффициентов регрессии, в то время как они в действительности являются случайными, нормально распределенными.
. Ошибки второго рода обусловлены фиксацией численного значения коэффициентов регрессии, в то время как они в действительности являются случайными, нормально распределенными.
Для линейной модели регрессии доверительный интервал рассчитывается следующим образом. Оценивается величина отклонения от линии регрессии (обозначим ее U):.
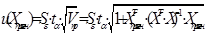 где
где
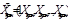
Проверка общего качества уравнения множественной регрессии
Для этой цели, как и в случае множественной регрессии, используется коэффициент детерминации R2:
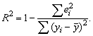
Справедливо соотношение 0<=R2<=1. Чем ближе этот коэффициент к единице, тем больше уравнение множественной регрессии объясняет поведение Y.
Для множественной регрессии коэффициент детерминации является неубывающей функцией числа объясняющих переменных. Добавление новой объясняющей переменной никогда не уменьшает значение R2, так как каждая последующая переменная может лишь дополнить, но никак не сократить информацию, объясняющую поведение зависимой переменной.
Иногда при расчете коэффициента детерминации для получения несмещенных оценок в числителе и знаменателе вычитаемой из единицы дроби делается поправка на число степеней свободы, т.е. вводится так называемый скорректированный (исправленный) коэффициент детерминации:
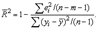
Соотношение может быть представлено в следующем виде:
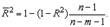
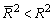 для m>1. С ростом значения m скорректированный коэффициент детерминации растет медленнее, чем обычный. Очевидно, что
для m>1. С ростом значения m скорректированный коэффициент детерминации растет медленнее, чем обычный. Очевидно, что 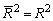 только при R2 = 1.
только при R2 = 1. 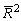 может принимать отрицательные значения.
может принимать отрицательные значения.
Доказано, что 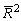 увеличивается при добавлении новой объясняющей переменной тогда и только тогда, когда t-статистика для этой переменной по модулю больше единицы. Поэтому добавление в модель новых объясняющих переменных осуществляется до тех пор, пока растет скорректированный коэффициент детерминации.
увеличивается при добавлении новой объясняющей переменной тогда и только тогда, когда t-статистика для этой переменной по модулю больше единицы. Поэтому добавление в модель новых объясняющих переменных осуществляется до тех пор, пока растет скорректированный коэффициент детерминации.
Рекомендуется после проверки общего качества уравнения регрессии провести анализ его статистической значимости. Для этого используется F-статистика:
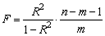
Показатели F и R2 равны или не равен нулю одновременно. Если F=0, то R2=0, следовательно, величина Y линейно не зависит от X1,X2,…,Xm.. Расчетное значение F сравнивается с критическим Fкр. Fкр, исходя из требуемого уровня значимости α и чисел степеней свободы v1 = m и v2 = n - m - 1, определяется на основе распределения Фишера. Если F>Fкр, то R2 статистически значим.
Для случая наличия в такой регрессии свободного члена коэффициент детерминации обладает следующими свойствами: [2]
1. принимает значения из интервала (отрезка) [0;1].
2. в случае парной линейной регрессионной МНК модели коэффициент детерминации равен квадрату коэффициента корреляции, то есть R2 = r2. А в случае множественной МНК регрессии R2 = r(y;f)2. Также это квадрат корреляции Пирсона между двумя переменными. Он выражает количество дисперсии, общей между двумя переменными.[3]
3. R2 можно разложить по вкладу каждого фактора в значение R2, причём вклад каждого такого фактора будет положительным. Используется разложение: 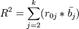 , где r0j - выборочный коэффициент корреляции зависимой и соответствующей второму индексу объясняющей переменной.
, где r0j - выборочный коэффициент корреляции зависимой и соответствующей второму индексу объясняющей переменной.
4. R2 связан с проверкой гипотезы о том, что истинные значения коэффициентов при объясняющих переменных равны нулю, в сравнении с альтернативной гипотезой, что не все истинные значения коэффициентов равны нулю. Тогда случайная величина 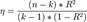 имеет F-распределение с (k-1) и (n-k) степенями свободы.
имеет F-распределение с (k-1) и (n-k) степенями свободы.
33.
После проверки адекватности, установления точности и надежности построенной модели её необходимо проанализировать. Для этого используют след показатели: 1. Частные коэффициенты эластичности , где а1 – коэффициент регрессии при соответствующем факторном признаке; - среднее значение соответствующего факторного признака; - среднее значение результативного признака. Коэффициент эластичности показывает на сколько процентов в среднем изменится значение результативного признака при изменении факторного признака на 1%. 2. Для определения тесноты связи между признаками при линейной форме связи используется показатель линейный коэффициент корреляции. Линейный коэффициент корреляции изменяется в пределах от -1 до 1. По этому показателю можно сделать след выводы: а) о направлении связи (если -1 < r < 0, то связь обратная, если 0 < r < 1, то связь прямая); б) определить тесноту связи.
27. Остаточная дисперсия и коэффициент детерминации R-квадрат. Чем меньше разброс значений остатков около линии регрессии по отношению к общему разбросу значений, тем, очевидно, лучше прогноз. Например, если связь между переменными X и Y отсутствует, то отношение остаточной изменчивости переменной Y к исходной дисперсии равно 1.0. Если X и Y жестко связаны, то остаточная изменчивость отсутствует, и отношение дисперсий будет равно 0.0. В большинстве случаев отношение будет лежать где-то между этими экстремальными значениями, т.е. между 0.0 и 1.0. 1.0 минус это отношение называется R-квадратом или коэффициентом детерминации. Это значение непосредственно интерпретируется следующим образом. Если имеется R-квадрат равный 0.4, то изменчивость значений переменной Y около линии регрессии составляет 1-0.4 от исходной дисперсии; другими словами, 40% от исходной изменчивости могут быть объяснены, а 60% остаточной изменчивости остаются необъясненными. В идеале желательно иметь объяснение если не для всей, то хотя бы для большей части исходной изменчивости. Значение R-квадрата является индикатором степени подгонки модели к данным (значение R-квадрата близкое к 1.0 показывает, что модель объясняет почти всю изменчивость соответствующих переменных). Матрица Гессе и стандартные ошибки. Матрицу частных производных второго порядка также часто называют матрицей Гессе. Оказывается, что обратная к ней матрица приблизительно равна матрице ковариаций оцениваемых параметров. Интуитивно понятно, что существует обратная зависимость между производными второго порядка по параметрам и их стандартными ошибками. Если изменить угловой коэффициент в точке минимума функции и сделать минимум функции более “резким”, то производные второго порядка увеличатся; при этом, оценки параметров будут практически стабильными в смысле, что параметры в точке минимума будут легко уточняемы. Если же производная второго порядка будет близка к нулю, то угол наклона в точке минимума будет практически неизменным, приводя к тому, что вы можете двигать параметры практически в любом направлении почти не изменяя значение функции потерь. Поэтому стандартные ошибки параметров будут очень большими.
Матрица Гессе и асимптотические стандартные ошибки для параметров вычисляются отдельно методом конечных разностей. Эта процедура возвращает очень точные асимптотические стандартные ошибки для всех методов оценивания.
34.Матрица парных коэффициентов корреляции
Более эффективным инструментом оценки мультиколлинеарности факторов является определитель матрицы парных коэффициентов корреляции между факторами  . При полном отсутствии корреляции
. При полном отсутствии корреляции  между факторами матрица парных коэффициентов корреляции между факторами — просто единичная матрица, ведь все недиагональные элементы в этом случае равны нулю. Напротив, если между факторами имеется полная линейная зависимость и все коэффициенты корреляции равны 1, то определитель такой матрицы равен 0. Следовательно, можно сделать вывод, что чем ближе к нулю определитель матрицы межфакторной корреляции
между факторами матрица парных коэффициентов корреляции между факторами — просто единичная матрица, ведь все недиагональные элементы в этом случае равны нулю. Напротив, если между факторами имеется полная линейная зависимость и все коэффициенты корреляции равны 1, то определитель такой матрицы равен 0. Следовательно, можно сделать вывод, что чем ближе к нулю определитель матрицы межфакторной корреляции  , тем сильнее мультиколлинеарность факторов и ненадежнее результаты множественной регрессии
, тем сильнее мультиколлинеарность факторов и ненадежнее результаты множественной регрессии  . Чем ближе к 1 этот определитель, тем меньше мультиколлинеарность
. Чем ближе к 1 этот определитель, тем меньше мультиколлинеарность  факторов.
факторов.
Если известно, что параметры уравнения множественной регрессии  линейно зависимы, то число объясняющих переменных в уравнении регрессии можно уменьшить на единицу. Если действительно использовать подобный прием, то можно повысить эффективность оценок регрессии. Тогда имевшаяся ранее мультиколлинеарность может быть смягчена. Даже если такая проблема и отсутствовала в исходной модели, то все равно выигрыш в эффективности может привести к улучшению точности оценок. Естественно, такое улучшение точности оценок отражается их стандартными ошибками. Сама линейная зависимость параметров называется также линейным ограничением
линейно зависимы, то число объясняющих переменных в уравнении регрессии можно уменьшить на единицу. Если действительно использовать подобный прием, то можно повысить эффективность оценок регрессии. Тогда имевшаяся ранее мультиколлинеарность может быть смягчена. Даже если такая проблема и отсутствовала в исходной модели, то все равно выигрыш в эффективности может привести к улучшению точности оценок. Естественно, такое улучшение точности оценок отражается их стандартными ошибками. Сама линейная зависимость параметров называется также линейным ограничением  .
.
Помимо уже рассмотренных вопросов нужно иметь в виду, что при использовании данных временного ряда необязательно требовать выполнения условия, что на текущее значение зависимой переменной влияют только текущие же значения объясняющих переменных. Можно ослабить это требование и исследовать, в какой степени проявляется запаздывание соответствующих зависимостей и такое влияние его. Спецификация запаздываний для конкретных переменных в данной модели называется лаговой структурой  (от слова «лаг»
(от слова «лаг»  — запаздывание). Такая структура бывает важным аспектом модели и сама может выступать в роли спецификации переменных модели. Поясним сказанное простым примером. Можно считать, что люди склонны соотносить свои расходы на жилье не с текущими расходами или ценами, а с предшествующими, например, за прошлый год.
— запаздывание). Такая структура бывает важным аспектом модели и сама может выступать в роли спецификации переменных модели. Поясним сказанное простым примером. Можно считать, что люди склонны соотносить свои расходы на жилье не с текущими расходами или ценами, а с предшествующими, например, за прошлый год.
