Озғалмалы координаттар өстеріндегі өзінің құраушылары арқылы берілген вектордың абсолют және салыстырмалы туындылары

Нүктенің күрделі қозғалысын әрі қарай қарастыру кезінде кез келген қозғалыстағы координаттар жүйесіне байланысты анықталған вектордан уақыт бойынша туынды алу мәселесі келіп туындайды. Міне, осыған байланысты вектордың абсолют және салыстырмалы туындылары деген ұғымдарды пайдалануымыз қажет болады. Осы ұғымдардың тиісті анықтамаларына тоқтап, одан соң вектордың абсолюттік туындысы мен салыстырмалы туындылары арсындағы байланыстарды табуымыз керек. 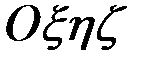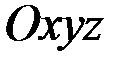Ол үшін қозғалмайтын координаттар жүйесі мен қатар, қған қарағанда, лездік бұрыштық жылдамдығы -ға тең сфералық қозғалыс жасайтын қозғалмалы координаттар жүйесі берілген дейік (2.30-сурет). Олардың бас нүктелері полюс О –да жататын болсын.

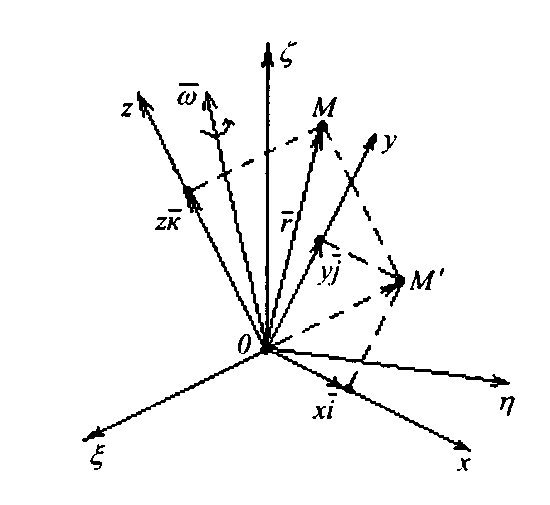
2.31-сурет

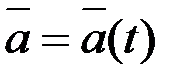Қандайда уақыт t –ға тәуелді өзгеретін вектор , Қозғалмалы координаттар жүйесіне қатысты алынған вектор болсын, яғни оның осы санақ жүйесінің өстеріндегі проекциялары белгілі уақыт функциялары болып келген дейік Демек, бұл вектор өзінің қозғалмалы өстердегі проекциялары арқылы жіктелген:

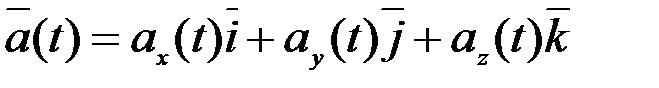. (2.108)

мұндағы векторларын тұрақты деп алынған сәттегі (2.108)-теңдікпен берілген. 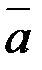векторынан уақыт бойынша алынған туындыны, вектордың салыстырмалы туындысы дейміз.

Салыстырмалы туындыны символымен белгілейміз. Сонда бұл анықтаманы өрнектейтін мынадай теңдік аламыз:

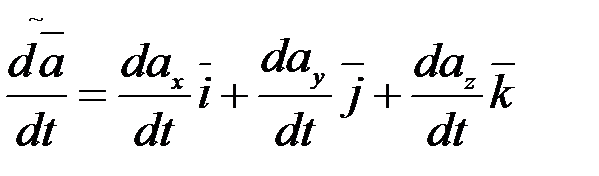. (2.109)

Бұл формула 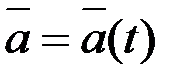векторының қозғалмалы координаттар жүйесіне қатысты өзгеру тездігін (жылдамдығын) көрсетеді. Осы формуладан вектордың өзегеру тездігі оның қозғалмалы өстердегі проекцияларының өзгеруіне тәуелді болып келетінін байқаймыз.

(2.108)-теңдіктің екі жағынан (2.109)-теңдікті ескере отырып уақыт бойынша толық туынды аламыз:

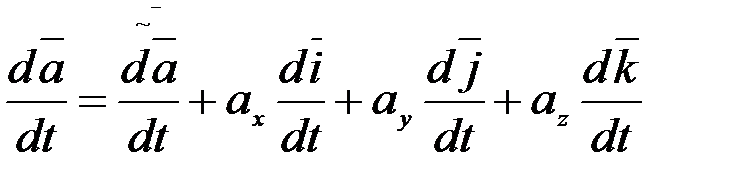. (2.110)

мұндағы бірлік векторлардан уақыт бойынша алынған туындыларды, қатты дене кинематикасында анықталған Эйлер формуласының көмегімен түрлендіреміз:

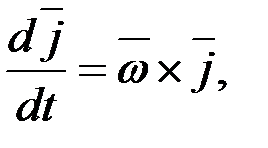
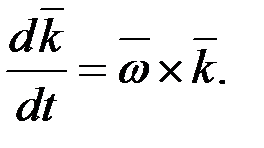(2.111)

(2.111) теңдіктерден (2.110) теңдігіндегі орындарына қоямыз:

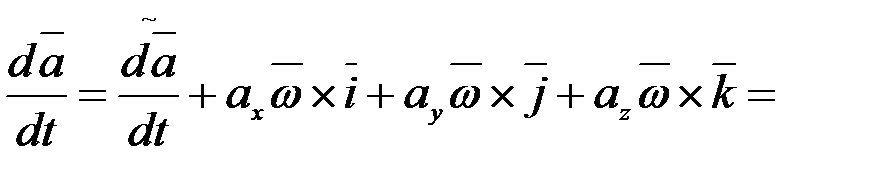
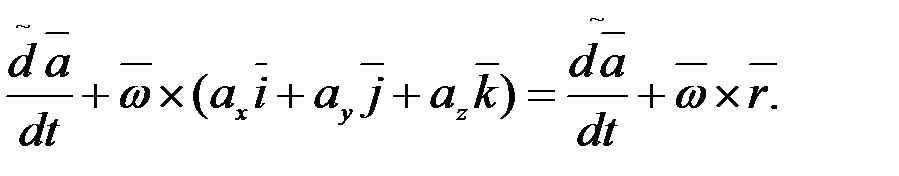
Сонымен, соңғы теңдіктен вектордың абсолюттік (толық) туындысы мен салыстырмалы (локальды) туындысын байланыстыратын мынадай формула аламыз:

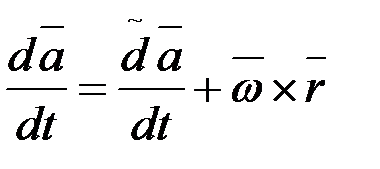. (2.112)

(2.112)- формуланы кинематиканың, вектордың салытырмалы туындысы жөніндегі, леммасы деп атайық. Мұндағы 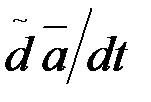вектор 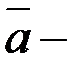ның салыстырмалы туындысы, ал 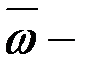қозғалмалы координаттар жүйесі 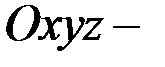тің полюс нүктесі арқылы өтетін өстен айналуының бұрыштық жылдамдығы. Осы айтылғандарды пайдалана отырып (2.112) формуласын мынадай лемма түрінде айта аламыз.

Лемма. Вектордың уақыт бойынша алынған абсолют туындысы сол вектордың салыстырмалы туындысына бұрыштық жылдамдық векторымен вектордың өзін векторлық түрде көбейтіп алып қосқанда шығатын векторға тең (2.112).

Осы тақырып соңында мынадай ескерту айтамыз. Кинематиканың салыстырмалы туынды туралы леммасы (2.108)-теңдік түріндегі жіктелуімен берілген векторлар үшін қолданылады. Салыстырмалы туынды ұғымы тек осындай векторларға арналған.