Арифметические команды

Сопроцессор использует шесть основных типов арифметических команд:

- Fxxx

Первый операнд берется из верхушки стека (источник), второй - следующий элемент стека. Результат выполнения команды записывается в стек

- Fxxx память

Источник берется из памяти, приемником является верхушка стека ST(0). Указатель стека ST не изменяется, команда действительна только для операндов с одинарной и двойной точностью

- Fixxx память

Аналогично предыдущему типу команды, но операндами могут быть 16- или 32-разрядные целые числа

- Fxxx ST, ST(i)

Для этого типа регистр ST(i) является источником, а ST(0) - верхушка стека - приемником. Указатель стека не изменяется

- Fxxx ST(i), ST

Для этого типа регистр ST(0) является источником, а ST(i) - приемником. Указатель стека не изменяется

- FxxxP ST(i), ST

Регистр ST(i) - приемник, регистр ST(0) - источник. После выполнения команды источник ST(0) извлекается из стека

Строка "xxx" может принимать следующие значения:

- ADD - Сложение

- SUB - Вычитание

- SUBR - Обратное вычитание, уменьшаемое и вычитаемое меняются местами

- MUL - Умножение

- DIV - Деление

- DIVR - Обратное деление, делимое и делитель меняются местами

Кроме основных арифметических команд имеются дополнительные арифметические команды:

- FSQRT - Извлечение квадратного корня

- FSCALE - Масштабирование на степень числа 2

- FPREM - Вычисление частичного остатка

- FRNDINT - Округление до целого

- FXTRACT - Выделение порядка числа и мантиссы

- FABS - Вычисление абсолютной величины числа

- FCHS - Изменение знака числа

По команде FSQRT вычисленное значение квадратного корня записывается в верхушку стека ST(0).

Команда FSCALE изменяет порядок числа, находящегося в ST(0). По этой команде значение порядка числа ST(0) складывается с масштабным коэффициентом, который должен быть предварительно записан в ST(1). Действие этой команды можно представить следующей формулой:

ST(0) = ST(0) * 2n, где -215 <= n <= +215

В этой формуле n - это ST(1).

Команда FPREM вычисляет остаток от деления делимого ST(0) на делитель ST(1). Знак результата равен знаку ST(0), а сам результат получается в вершине стека ST(0).

Действие команды заключается в сдвигах и вычитаниях, аналогично ручному делению "в столбик". После выполнения команды флаг C2 регистра состояния может принимать следующие значения:

- 0 - Остаток от деления, полученный в ST(0), меньше делителя ST(1), команда завершилась полностью

- 1 - ST(0) содержит частичный остаток, программа должна еще раз выполнить команду для получения точного значения остатка

Команда RNDINT округляет ST(0) в соответствии с содержимым поля RC управляющего регистра.

Команда FABS вычисляет абсолютное значение ST(0). Аналогично, команда FCHS изменяет знак ST(0) на противоположный.

Трансцендентные команды

Трансцендентные команды предназначены для вычисления следующих функций:

- тригонометрические (sin, cos, tg,...)

- обратные тригонометрические (arcsin, arccos,...)

- показательные (xy, 2x, 10x, ex)

- гиперболические (sh, ch, th,...)

- обратные гиперболические (arsh, arch, arcth,...)

Вот список всех трансцендентных команд математического сопроцессора:

- FPTAN Вычисление частичного тангенса

- FPATAN Вычисление частичного арктангенса

- FYL2X Вычисление y*log2(x)

- FYL2XP1 Вычисление y*log2(x+1)

- F2XM1 Вычисление 2x-1

- FCOS Вычисление cos(x)

- FSIN Вычисление sin(x)

- FSINCOS Вычисление sin(x) и cos(x) одновременно

Команда FPTAN вычисляет частичный тангенс ST(0), размещая в стеке такие два числа x и y, что y/x = tg(ST(0)).

После выполнения команды число y располагается в ST(0), а число x включается в стек сверху (то есть записывается в ST(1)). Аргумент команды FPTAN должен находится в пределах:

0 <= ST(0) <= pi/4

Пользуясь полученным значением частичного тангенса, можно вычислить другие тригонометрические функции по следующим формулам:

- sin(z) = 2*(y/x) / (1 + (y/x)2)

- cos(z) = (1 - (y/x)2) / (1 + (y/x)2)

- tg(z/2) = y/x;

- ctg(z/2) = x/y;

- cosec(z) = (1 + (y/x)2) / 2*(y/x)

- sec(z) = (1 + (y/x)2) / (1 - (y/x)2)

Где z - значение, находившееся в ST(0) до выполнения команды FPTAN, x и y - значения в регистрах ST(0) и ST(1), соответственно.

Команда FPATAN вычисляет частичный арктангенс:

z=arctg(ST(0)/ST(1))=arctg(x/y).

Перед выполнением команды числа x и y располагаются в ST(0) и ST(1), соответственно. Аргументы команды FPATAN должен находится в пределах:

0 < y < x

Результат записывается в ST(0).

Команда FYL2X вычисляет выражение y*log2(x), операнды x и y размещаются, соответственно, в ST(0) и ST(1). Операнды извлекаются из стека, а результат записывается в стек. параметр x должен быть положительным числом.

Пользуясь результатом выполнения этой команды, можно вычислить следующим образом логарифмические функции:

- Логарифм по основанию два: log2(x) = FYL2(x)

- Натуральный логарифм: loge(x) = loge(2) * log2(x) = FYL2X(loge(2), x) = FYL2X(FLDLN2, x)

- Десятичный логарифм: log10(x) = log10(2) * log2(x) = FYL2X (log10(2), x) = FYL2X(FLDLG2, x)

Функция FYL2XP1 вычисляет выражение y*log2(x+1), где x соответствует ST(0), а y - ST(1). Результат записывается в ST(0), оба операнда выталкиваются из стека и теряются.

На операнд x накладывается ограничение: 0 < x < 1 - 1/sqrt(2)

Команда F2XM1 вычисляет выражение 2x-1, где x - ST(0). Результат записывается в ST(0), параметр должен находиться в следующих пределах: 0 <= x <= 0,5

Команда FCOS вычисляет cos(x). Параметр x должен находиться в ST(0), туда же записывается результат выполнения команды.

Команда FSIN аналогична команде FCOS, но вычисляет значение синуса ST(0).

Команда FSINCOS вычисляет одновременно значения синуса и косинуса параметра ST(0). Значение синуса записывается в ST(1), косинуса - в ST(0).

Константы FPU

FLD1 - Поместить в стек 1,0

FLDZ - Поместить в стек +0,0

FLDPI - Поместить в стек число π

FLDL2E - ­­Поместить в стек log2(e)

FLDL2T - Поместить в стек log2(10)

FLDLN2 - Поместить в стек ln(2)

FLDLG2 - Поместить в стек lg(2)

Все эти команды помещают в стек (то есть уменьшают ТОР на один и помещают в ST(0)) соответствующую часто используемую константу.

Пример

Пример вычисления выражения:

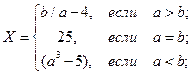
Анализ особенностей задачи.

Возможны две ситуации деления на ноль:

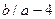• , если 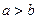. Например, .

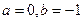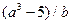• , если 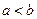. Например, .

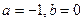В то же время ситуация, когда 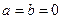, является допустимой.

.Model Small

.586

.Data

res dq 0

a dq 3.0

b dq 10.0

const25 dw 25

const4 dw 4

const5 dw 5

status dw 0

.Code

;Вывод вещественного числа

; аргумент - количество цифр дробной части

length_frac Equ [BP+4]

; локальные переменные

ten Equ word ptr [BP-2]

temp Equ word ptr [BP-4]

OutFloat Proc Near

ENTER 4, 0 ; выделим в кадре стека 4 байта под локальные переменные

MOV ten, 10

ftst ; определяем знак числа

fstsw AX

SAHF

JNC @positiv

MOV AL, '-' ; если число отрицательное - выводим минус

INT 29h

fchs ; и получаем модуль числа

@positiv:

fld1 ; загружаем единицу

fld st(1) ; копируем число на вершину стека

fprem ; выделим дробную часть

fsub st(2), st ; отнимем ее от числа - получим целую часть

fxch st(2) ; меняем местами целую и дробную части

XOR CX, CX ; обнуляем счетчик

; далее идет стандартный алгоритм вывода целого числа на экран

@1:

fidiv ten ; делим целую часть на десять

fxch st(1) ; обменяем местами st и st(1) для команды fprem

fld st(1) ; копируем результат на вершину стека

fprem ; выделим дробную часть (цифру справа от целой части)

fsub st(2), st ; получим целую часть

fimul ten ; *10

fistp temp ; получаем очередную цифру

PUSH temp ; заталкиваем ее глубже в стек

INC CX ; и увеличим счетчик

fxch st(1) ; подготовим стек к следующему шагу цикла (полученное частное на вершину, в st(1) - 1)

ftst ; проверим не получили ли в частном 0?

fstsw AX

SAHF

JNZ @1 ; нет - продолжим цикл

@2: ; извлекаем очередную цифру, переводим её в символ и выводим.

POP AX

ADD AL, '0'

INT 29h

LOOP @2

; далее то же самое, только для дробной части. Алгоритм похож на вывод целого числа, только вместо деления умножение и проход по числу слева

fstp st ; сначала проверим, есть ли дробная часть

fxch st(1)

ftst

fstsw AX

SAHF

JZ @quit ; дробная часть отсутствует

MOV AL, '.'

INT 29h ; если присутствует - выведем точку

MOV CX, length_frac ; помещаем в счетчик длину дробной части

@3:

fimul ten ; умножим на 10

fxch st(1) ; подготовка для fprem - меняем st и st(1) местами и

fld st(1) ; копируем число на вершину

fprem ; отделим дробную часть от целой

fsub st(2), st ; и оставляем дробную

fxch st(2)

fistp temp ; выталкиваем полученное число из стека в temp

MOV AX, temp ; по дробной части идем слева, значит число выводим сразу, без предварительного сохранения в стек

OR AL, 30h ; перевод в ascii

INT 29h ; на экран

fxch st(1) ; подготовим стек к следующему шагу цикла (полученное частное на вершину, в st(1) - 1)

ftst

fstsw AX

SAHF ; проверим на 0 остаток дробной части

LOOPNE @3

@quit:

fstp ; готово. Чистим стек сопроцессора

fstp st

LEAVE ; эпилог

RET 2

OutFloat EndP

func Proc Far

;PUSHA

finit ; инициализация сопроцессора

fld qword ptr[b]; b

fld qword ptr[a]; a b

fcom st(1); сравниваем a и b

fstsw status; сохраняем регистр флагов сопроцессора

MOV AH, byte ptr [status+1]

SAHF ; записываем в регистр флагов процессора

JA a_bigger; переход если a больше

JB b_bigger; переход если b больше

; если равны

fild const25; 25 a b

JMP endcalc

a_bigger: ftst; сравнение a с 0

fstsw status; сохраняем регистр флагов сопроцессора

MOV AH, byte ptr [status+1]

SAHF ; записываем в регистр флагов процессора

JE error; переход если a=0

fdivp st(1), st(0); b/a

fild const4; 4 b/a

fsubp st(1), st(0); b/a-4

JMP endcalc

b_bigger: fldz; 0 a b

fcomp st(2); сравнение b с 0

; a b

fstsw status; сохраняем регистр флагов сопроцессора

MOV AH, byte ptr [status+1]

SAHF ; записываем в регистр флагов процессора

JE error; переход если b=0

fld st(0); a a b

fmul st(1), st(0); a a*a b

fmulp st(1), st(0); a*a*a b

fild const5 ; 5 a*a*a b

fsubp st(1), st(0); a*a*a-5 b

JMP endcalc

error:

fldz; формируем результат ошибки

endcalc:

fstp res; сохранение результата

RET

func EndP

start:

MOV AX, @data

MOV DS, AX

CALL func

XOR AX,AX

XOR BX,BX

XOR CX,CX

XOR DX,DX

finit; инициализируем сопроцессор

fld res; записываем число стека для вывода

PUSH 10; заталкиваем число знаков после запятой

CALL outfloat

MOV AX,4c00h

INT 21h

End start