Расчёт пусковой критической концентрации борной кислоты

ВВЭР ПРИ ЕГО ЭКСПЛУАТАЦИИ

Ядерный реактор, как следует из всего рассмотренного ранее, является достаточно опасным инженерным сооружением. Именно поэтому оператору всякий раз, прежде чем браться за ключи управления, требуется представить, как реактор отзовётся на предпринимаемое воздействие и к чему может привести это воздействие. Разумеется, в процессе накопления управленческого опыта оператор приобретает некоторые навыки, позволяющие ему действовать без больших умственных нагрузок, почти автоматически, будучи уверенным при этом, что ничего серьёзного или опасного для реактора эти действия не повлекут.

Однако, безошибочность действий оператора, как принято считать, имеет свои пределы. Поэтому реакторная установка, которая принципиально менее сложна, чем самый обыкновенный двигатель внутреннего сгорания, оснащается превеликим множеством различных блокировок и защит, предотвращающих возможность из ошибки оператора возникнуть аварийной ситуации, могущей привести к тяжёлым последствиям.

Расчёт пусковой критической концентрации борной кислоты

Реакторная установка энергоблока АЭС с ВВЭР тем успешнее оправдывает своё назначение экономически, чем на более высоком уровне мощности непрерывно работает реактор в течение всей кампании. Это понятно: всякое понижение уровня мощности и, тем более, останов реактора на некоторое время влечёт за собой недовыработку отдаваемой в сеть электрической мощности. Поэтому останов энергоблока в процессе кампании – это всегда вынужденный останов (вследствие возникновения аварийной ситуации), и время стоянки реактора должно быть сокращено до минимума: как только причины останова реактора устраняются, реактор пускается вновь самым срочным порядком, чтобы энергоблок работал и выдавал электроэнергию.

Об этом упомянуто лишь для того, чтобы отметить как факт: стоянки реактора АЭС во время кампании, как правило, кратковременны (не более трёх суток), после чего всегда сразу следует пуск.

Пуск ВВЭР – операция приведения реактора из подкритического состояния в критическое путём снижения концентрации борной кислоты в теплоносителе первого контура от стояночного значения до величины, при которой реактор становится критическим. Эта величина и называется пусковой концентрацией борной кислоты.

Расчёт пусковой концентрации борной кислоты основывается на знании величины концентрации её в контуре в ближайший предшествующий по времени момент, когда реактор был последний раз критичен – в момент предшествующего пуску останова реактора. При этом подразумевается, что основные характеристики состояния реактора в момент останова известны. То есть известны:

С_о, г/кг – концентрация борной кислоты в теплоносителе первого контура в момент останова;

N_p, % N_p^ном – уровень мощности, на котором работал последние трое суток перед остановом реактор;

W, э.с. – энерговыработка реактора в момент останова;

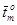, ^оС – средняя температура теплоносителя в в реакторе в момент останова;

Н_о, % - положение рабочей группы ОР СУЗ в момент останова.

Кроме того, известны основные параметры состояния реактора в момент предстоящего пуска, а именно:

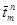, ^оС – средняя температура теплоносителя в реакторе в момент пуска;

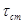, час – время стоянки реактора (от момента останова до момента пуска);

Н_п, % - положение рабочей группы ОР СУЗ в момент предстоящего пуска.

*) Относительно Н_п уместно сразу отметить, что в соответствии с правилами, зафиксированными в Технологическом Регламенте по безопасной эксплуатации реакторной установки, при пуске рабочая группа устанавливается в положение её максимальной эффективности. Это положение изменяется в процессе кампании. Поэтому рекомендации ТРБЭ по пусковому положению рабочей группы для различных топливных загрузок ВВЭР даются в зависимости от периода кампании. Например, для 5-й топливной загрузки ВВЭР-1000 1-го энергоблока ХАЭС рекомендуется при энерговыработках W < 200 э.с. пусковое положение рабочей (10-й) группы Н_п = 40% её хода от низа активной зоны, а при W ³ 200 э.с. – 60 %.

23.1.1. Теоретические основы расчёта. Поскольку в оба рассматриваемых момента (в момент останова и в момент пуска) реактор находится в критическом состоянии, то в обоих случаях его реактивность r = 0. И, следовательно, изменение реактивности за период времени между остановом и пуском Dr = 0.

Все происходящие за этот период времени изменения реактивности реактора обусловлены следующими физическими процессами:

а) Переотравлением реактора ксеноном. В момент останова реактор после длительной работы на постоянном уровне мощности N_p^o был стационарно отравлен ксеноном на этом уровне мощности. После останова реактора, как известно, начинается нестационарное его переотравление («йодная яма»), и, если время стоянки реактора до пуска не превышает трёх суток, полностью (до нуля) реактор разотравиться не успеет. В этом случае величина переотравления Dr_Хе находится по графику йодной ямы после останова реактора с заданного уровня мощности 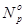по времени стоянки реактора t_ст.

Если же время стоянки реактора после останова превышает трое суток, то за это время он полностью разотравится, то есть изменение реактивности за счёт переотравления ксеноном в этом случае будет равно

Dr_Хе = 0 - 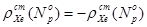, (23.1)

и величина стационарного отравления 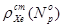в этом случае снимается с кривой стационарных отравлений реактора, действительной в заданный момент кампании.

б) Температурным изменением реактивности за счёт того, что средние температуры теплоносителя в реакторе в моменты останова и пуска не одинаковы (как правило, после останова реактор начинает расхолаживаться). Температурное изменение реактивности рассчитывается по формуле:

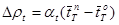, (23.2)

где a_t, %/^оС – температурный коэффициент реактивности теплоносителя, снимаемый с графика a_t=f(W) для данного момента кампании W.

*) Заметим, что, поскольку величина температурного коэффициента реактивности теплоносителя в любой момент кампании – величина отрицательная, а 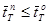, температурное изменение реактивности всегда получается величиной положительной.

в) Мощностным изменением реактивности, поскольку в момент останова реактор был на уровне мощности 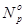, а в момент пуска он достигает критичности на нулевом уровне мощности. Величина мощностного изменения реактивности равна:

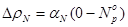, (23.3)

где величина мощностного коэффициента реактивности 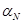, %/МВт, как и величина ТКР теплоносителя снимается с графика 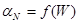для значения энерговыработки W, соответствующей данному моменту кампании.

г) Изменением реактивности за счёт неодинакового положения рабочей группы ОР СУЗ в моменты пуска и останова. Эта величина находится как разница интегральных эффективностей рабочей группы в моменты пуска и останова:

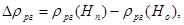(23.4)

снимаемой с кривой интегральной эффективности рабочей группы ОР СУЗ для данного момента кампании.

*) Поскольку аксиальная составляющая нейтронного поля в реакторе изменяется в процессе кампании, - изменяется и кривая интегральной эффективности рабочей группы. Обычно в распоряжении оператора есть две расчётные кривые интегральной эффективности рабочей группы – на момент начала кампании и на момент конца кампании. Поэтому для более точного расчёта величины 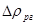следует прибегнуть к двойной линейной интерполяции: найти вначале точное значение 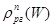для данного момента кампании W:

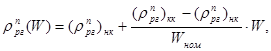(23.5)

где W, э.с. – текущее (данное) значение энерговыработки загрузки реактора;

W_ном, э.с. – номинальное (расчётное) значение энерговыработки загрузки;

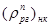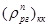и , % - значения интегральной эффективности рабочей группы ОР СУЗ в начале и конце кампании, снимаемые с кривых интегральной эффективности рабочей группы соответственно для начала и конца кампании загрузки активной зоны.

Точно такая же операция проделывается и для величины :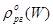

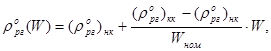(23.6)

после чего значения 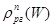и 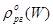подставляются в формулу (23.4).

д) Изменением реактивности за счёт разницы концентраций борной кислоты в теплоносителе первого контура в моменты останова и пуска реактора. Эта величина находится по формуле:

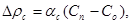(23.7)

где a_с, %/г/кг – величина дифференциальной эффективности борной кислоты в рассматриваемый момент кампании, находимая имеющихся в распоряжении оператора таблиц или графиков зависимости этой величины от энерговыработки W;

С_п и С_о, г/кг – величины концентраций борной кислоты при пуске и останове реактора соответственно.

е) Нестационарным переотравлением реактора самарием за время стоянки. Если реактор после останова бездействует достаточно длительное время (более 5 суток), то он, как известно, попадает в «прометиевый провал», а если стоянка длится более 10 суток, - он достигает «дна прометиевого провала». Как уже отмечалось, этот случай совершенно нетипичен для практики эксплуатации реакторов АЭС, но всё же полностью его возможность не исключается. Для нахождения нестационарного переотравления реактора самарием за время длительной стоянки необходимо знать:

- средний уровень мощности, на котором реактор работал последние 10 суток перед остановом ,% ;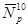

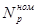- время стоянки реактора t_ст, час.

Величина переотравления в момент t_ст после останова находится по формуле:

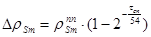, (23.8)

где 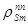, % - полная глубина прометиевого провала после останова с уровня мощности 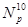, находимая по формуле: 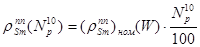, (23.9)

поскольку глубина прометиевого провала линейно зависит от мощности реактора. Здесь 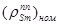, % - глубина прометиевого провала после останова реактора с уровня мощности 100% в рассматриваемый момент кампании. Эта величина не изменяется процессе кампании и для разных загрузок ВВЭР-1000 лежит в довольно узких пределах: от (-0.28) до (- 0.30) %. Конкретная цифра для своей установки известна каждому оператору, поскольку она является одной из характеристик реакторной установки.

*) Если время стоянки реактора составляет 1 сутки = 24 часа, то Dr_Sm » 0.27 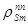, при времени стоянки 2 суток 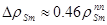, а при 3 суточной стоянке 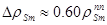. То есть даже после останова реактора с полной мощности в течение первых трёх суток стоянки величины переотравления реактора самарием не превышают (- 0.18%), что при определении пусковой концентрации борной кислоты, как будет ясно далее, является пренебрежимо малой величиной. Вот почему, если время стоянки реактора не превышает 3 суток после останова, величина Dr_Sm в расчётах обычно не учитывается.

Итак, с учётом последнего замечания

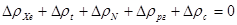(23.10)

Обозначая для краткости сумму первых четырёх слагаемых как 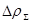, имеем:

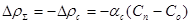(23.11)

Выражение (23.11) недвусмысленно говорит о том, что алгебраическая сумма изменений реактивности от первых четырёх эффектов (переотравления ксеноном, температурного изменения реактивности, мощностного изменения реактивности и изменения реактивности за счёт неодинакового положения рабочей группы ОР СУЗ при останове и пуске реактора), проявляющихся за время стоянки реактора, должна быть компенсирована противоположным по знаку изменением реактивности за счёт изменения концентрации борной кислоты. Разрешая (23.11) относительно искомой С_п, имеем:

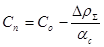(23.12)

23.1.2. Алгоритм расчёта пусковой концентрации борной кислоты. Исходя из сказанного в п.23.1.1, алгоритм расчёта пусковой концентрации борной кислоты при пуске реактора ВВЭР после не более чем трёхсуточной стоянки выглядит так.

1) Величина переотравления реактора ксеноном 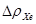- снимается с графика йодной ямы по величине среднего уровня мощности реактора 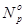, на котором он работал последние трое суток перед остановом, и времени стоянки реактора t_ст.

2) Изменение реактивности реактора в период стоянки за счёт изменения средней температуры теплоносителя в реакторе

,

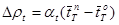где величина температурного коэффициента реактивности теплоносителя a_t снимется с графика расчётной зависимости a_t = f(W) для величины знерговыработки W, соответствующей моменту останова реактора.

3) Мощностное изменение реактивности реактора после останова реактора

,

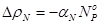где величина 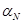, %/МВт снимается с графика расчётной зависимости 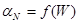по величине энерговыработки W на момент останова реактора. Величина мощности реактора в момент останова в формулу должна быть подставлена в МВт, а если (как это чаще всего и бывает) уровень мощности реактора в момент останова задан в % 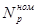, то расчётная формула будет иметь вид:

,

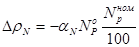где величина номинальной мощности реактора 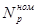подставляется в МВт.

*) Ещё раз обращается внимание на то, что знак «минус» в этих выражениях – формульный знак, и если учесть, что величина мощностного коэффициента реактивности – также отрицательная величина, то величина мощностного изменения реактивности в задаче о расчёте пусковой концентрации борной кислоты – всегда положительна.

4) Изменение реактивности реактора за счёт неодинаковости положения рабочей группы ОР СУЗ при останове и пуске реактора. Как уже указывалось в п.23.1.1, рассчитывается по формуле

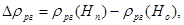
в которую подставляются интегральные эффективности рабочей группы в пусковом положении и в положении при останове реактора, снимаемые с кривой интегральной эффективности рабочей группы на момент кампании W, когда пускается реактор. При наличии расчётных кривых интегральной эффективности на моменты начала и конца кампании следует пользоваться линейной интерполяцией значений интегральной эффективности, как об этом говорилось в п.23.1.1.

5) Суммарное изменение реактивности 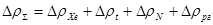- находится как алгебраическая сумма всех указанных изменений реактивности, то есть с учётом знаков этих изменений.

6) Величина дифференциальной эффективности борной кислоты a_с, %./г/кг в рассматриваемый момент кампании W – находится как функция W по таблицам или по графикам, имеющимся в распоряжении оператора.

7) Пусковая концентрация борной кислоты – находится по формуле:

.

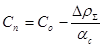*) Будучи достаточно внимательным, строго соблюдая правила знаков, вы можете быть уверены в правильности расчёта С_п по приведенному алгоритму. И всё же нелишне в процессе расчётов контролировать себя, чтобы не упускать из вида физического смысла того, что рассчитывается. Если величина любого изменения Dr имеет положительный знак – речь идёт о высвобождении положительной реактивности в результате действия рассматриваемого эффекта. Если величина Dr отрицательна – в результате действия рассматриваемого эффекта реактивность теряется.

Самоконтроль особенно важен на заключительной стадии расчёта. Если величина суммарного изменения реактивности положительна, это означает, что за время стоянки реактора высвободилась положительная реактивность, и компенсация её может быть достигнута только одним путём – увеличением концентрации борной кислоты при пуске. То есть величина С_п должна получаться большей, чем С_о. Если же величина Dr_S < 0, то за время стоянки реактора в нём происходит потеря реактивности, для компенсации которой потребуется уменьшить концентрацию борной кислоты при пуске, то есть С_п < С_о.

Точно к таким же выводам приводит рассмотрение последней формулы для расчёта С_п, если принять во внимание, что величина a_с по смыслу своему – отрицательная.