Основные теоретические положения. Совокупность трех электрических цепей, в которых действуют синусоидальные ЭДС одинаковой частоты, отличающиеся по фазе одна от другой на 2p/3 и индуктируемые
Совокупность трех электрических цепей, в которых действуют синусоидальные ЭДС одинаковой частоты, отличающиеся по фазе одна от другой на 2p/3 и индуктируемые в одном источнике энергии, называется трехфазной системой или трехфазной цепью.
Трехфазная цепь состоит из трех основных частей или элементов: трехфазного генератора, создающего трехфазную систему ЭДС; линии передачи со всем необходимым оборудованием; приемников (потребителей), которые могут быть как трехфазными (например, электродвигатель), так и однофазными (например, лампы накаливания).
Трехфазный генератор состоит из статора и ротора (индуктора). На статоре генератора размещается обмотка, состоящая из трех частей или, как принято их называть, фаз. Обмотки фаз располагаются на статоре таким образом, чтобы их магнитные оси были сдвинуты относительно друг друга на угол 2p/3. На рис.1 каждая фаза обмотки статора условно показана состоящей из одного витка. Начала обмоток обозначаются буквами А, В, С, а концы – X, Y, Z. Аналогично и фазы генератора называются А, В, С. Ротором трехфазного генератора является электромагнит постоянного тока.
При вращении ротора с угловой скоростью w в фазных обмотках статора возбуждаются ЭДС индукции еА , еВ , еС одинаковой амплитуды Еm и частоты w, но сдвинутые по фазе относительно друг друга на 2p/3 вследствие их пространственного смещения. Такая система ЭДС называется симметричной.
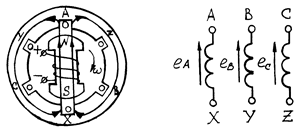
Рис.1 Рис.2
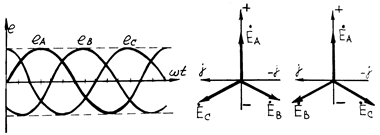
А б
Рис.3 Рис.4
На схемах обмотки (или фазы) источника питания обозначают так, как показано на рис.2.
За условно положительное направление ЭДС в каждой фазе принимают направление от конца к началу.
Трехфазная симметричная система ЭДС может изображаться графиками, тригонометрическими функциями, векторами и функциями комплексного переменного. Графики изменения ЭДС симметричной системы показаны на рис.3. Если начальную фазу ЭДС фазы АХ принять равной нулю, то тригонометрическая форма представления трехфазной симметричной системы ЭДС (прямой последовательности) имеет вид еА = Еm sin wt ; еВ= Еm sin (wt – 2p/3)
еС = Еm sin (wt – 4p/3) = Еm sin (wt + 2p/3) .
Комплексная форма записи:
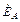 = Е ;
= Е ; 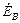 = Е
= Е 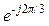 ;
;  = Е
= Е 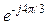 = Е
= Е 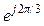 ,
,
где 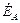 ,
, 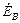 ,
,  - комплексы действующих значений ЭДС;
- комплексы действующих значений ЭДС;
Е – действующее значение ЭДС: Е = 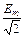 .
.
Для такой системы справедливы соотношения:
еА + еВ + еС = 0 ;
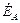 +
+ 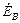 +
+  = 0 .
= 0 .
Векторная диаграмма трехфазной симметричной системы ЭДС показана на рис.4: а – прямая последовательность фаз; б – обратная последовательность фаз. Последовательность фаз определяет направление вращения трехфазных двигателей, ее нужно учитывать также при включении трехфазных генераторов на параллельную работу. Для определения последовательности фаз служат фазоуказатели.
Обмотки фаз генератора обычно соединяют звездой, то есть концы обмоток X, Y, Z соединяют в общую точку N, называемую нулевой или нейтральной (рис.5). При этом от трехфазного генератора отходят 4 провода – три линейных А, В, С и нейтральный N – n. В трехфазных четырехпроводных сетях нейтральный провод заземляют.
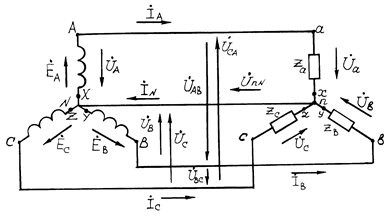
Рис.5
Однофазные приемники также могут соединяться звездой, то есть их концы x, y, z соединяют в общую точку n и присоединяют к нейтральному проводу, а к свободным началам фаз а, в, с подводят энергию по линейным проводам от трехфазного генератора.
 Напряжения UA , UB , UC между линейными и нейтральными проводами, то есть между началом и концом фазы, называются фазными. Напряжения между соответствующими линейными проводами UAB , UBC , UCA , то есть между началами фаз, называются линейными. Эти напряжения связаны между собой соотношениями:
Напряжения UA , UB , UC между линейными и нейтральными проводами, то есть между началом и концом фазы, называются фазными. Напряжения между соответствующими линейными проводами UAB , UBC , UCA , то есть между началами фаз, называются линейными. Эти напряжения связаны между собой соотношениями:
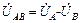 ;
; 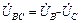 ;
;
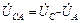 ;
;
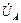 +
+ 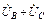 = 0 ;
= 0 ;
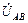 +
+ 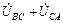 = 0 .
= 0 .
Рис.6
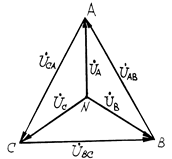
На рис.6 показана векторная диаграмма линейных и фазных напряжений генератора. Из диаграммы видно, что для симметричной системы напряжений между фазными и линейными напряжениями существует зависимость
Uл = 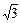 Uф » 1,73Uф .
Uф » 1,73Uф .
Токи IA , IB , IC , протекающие в линейных проводах, называются линейными. Токи, протекающие в обмотках генератора или фазах приемника, называются фазными. При соединении звездой фазные и линейные токи равны:
Iл = Iф .
Применяя к узлу n (рис.5) первый закон Кирхгофа, получаем ток в нулевом проводе:
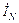 =
= 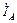 +
+ 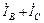 . (1)
. (1)
Приемники называются симметричными, если комплексные сопротивления их фаз Za = Za 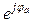 ; Zв = Zв
; Zв = Zв 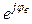 ; Zс = Zс
; Zс = Zс 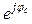 равны между собой, то есть равны полные сопротивления отдельных фаз:
равны между собой, то есть равны полные сопротивления отдельных фаз:
Za= Zв = Zс= Zф (2)
и одинаковы углы сдвига фаз:
jа = jв = jс = jф . (3)
Если одно из условий симметрии, характеризующее равномерность (2) или неоднородность (3) нагрузки, не выполняется, приемники называются несимметричными.
Сдвиг по фазе между током и напряжением jф = yu – yi на приемнике зависит от вида нагрузки (табл. 1) и определяется из треугольника сопротивлений фазы нагрузки. Например, для фазы с активно-индуктивной нагрузкой комплексное сопротивление равно:
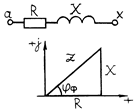 Zф = R + jX = Zф
Zф = R + jX = Zф 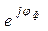 ,
,
где Zф = 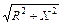 - полное сопротивление фазы;
- полное сопротивление фазы;
jф = arctg 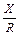 - угол сдвига между током и (4) . напряжением
- угол сдвига между током и (4) . напряжением
Таблица 1
| Вид нагрузки | Схема замещения | Векторная диаграмма |
| Активная |  | 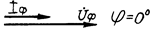 |
| Индуктивная |  | 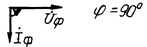 |
| Емкостная | 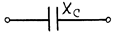 | 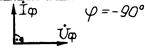 |
| Активно-индуктивная | 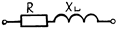 | 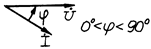 |
Применяя для трехфазной цепи, соединенной звездой (рис.5), метод двух узлов, получаем 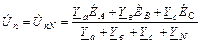 , (5)
, (5)
где
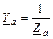 ;
; 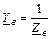 ;
; 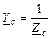 ;
; 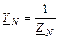 -
-
комплексные проводимости фаз нагрузки с учетом сопротивления линейных проводов и нейтрального провода, если сопротивлением проводов нельзя пренебречь.
При симметричной нагрузке Ya = Yв = Yс = Yф , а
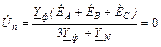
ток в каждой фазе приемника Iф =  одинаков, ток в нейтральном проводе
одинаков, ток в нейтральном проводе 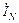 = 0 . Это позволяет выполнить трехфазную линию трехпроводной.
= 0 . Это позволяет выполнить трехфазную линию трехпроводной.
Векторная диаграмма для напряжений и токов при активно-индуктивной симметричной нагрузке показана на рис.7.
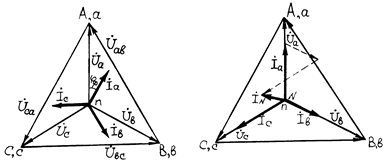
Рис.7 Рис.8
Если сопротивлением проводов можно пренебречь, то ZN = 0, YN = ¥ . При этом напряжение между нейтралями генератора и нагрузки 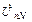 = 0. Фазные напряжения нагрузки равны соответствующим напряжениям генератора, т.е. остаются симметричными при любой несимметричной нагрузке (например, неравномерной активной, рис.8):
= 0. Фазные напряжения нагрузки равны соответствующим напряжениям генератора, т.е. остаются симметричными при любой несимметричной нагрузке (например, неравномерной активной, рис.8):
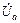 =
= 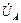 ;
; 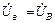 ;
;  ;
; 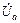 =
= 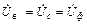 .
.
Ток в нейтральном проводе равен: 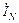 =
= 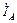 +
+ 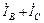 .
.
Отсутствие нейтрального провода, т.е. ZN = ¥ , YN = 0 значительно нарушает симметрию фазных напряжений нагрузки, появляется смещение между нейтралями генератора и нагрузки 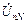 (рис.9).
(рис.9).
Комплексные значения напряжений на нагрузке можно определить по соотношениям:
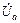 =
= 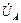 -
- 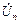 ;
;
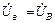 -
- 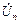 ;
;
 -
- 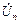 .
.
Фазные токи равны линейным:
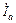 =
= 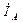 =
= 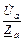 ;
; 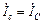 =
= 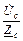 ;
; 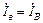 =
= 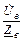 ;
;
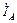 +
+ 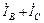 = 0.
= 0.
Понятие мощности, потребляемой каждой из фаз приемника, дано в лабораторной работе №1 (п.4).
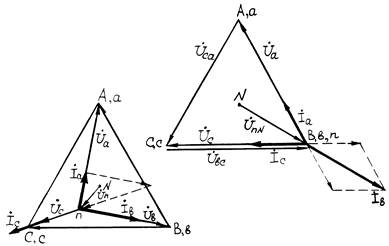
Рис.9 Рис.10
