Формальный анализ высказываний

В настоящем разделе мы возвращаемся к формальному анализу составных высказываний, начатому в главе 1. Введённые в этой главе булевы функции, таблицы истинности и связанные с ними понятия оказываются очень удобным инструментом для такого анализа.

В разделе 1-3 было продемонстрировано, как формально описать составное высказывание с помощью более короткого выражения. В это выражение входят символы простых высказыва-ний, из которых образовано данное составное высказывание, а также соединяющие их знаки операций над высказываниями. Входят, если необходимо, и скобки, которые указывают поря-док выполнения этих операций, подобно тому, как скобки указывают порядок выполнения алге-браических и арифметических операций в «школьной» математике. Все шесть возможных опе-раций над высказываниями и их истинностными значениями (Ø, Ù, Ú, →, Å, 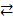) подробно определены и объяснены в разделе 1-2.1.

Исходя из формальной записи составного высказывания, можно получить его новое пред-ставление – сопровождающую высказывание булеву формулу и реализуемую ей булеву функ-цию. Опишем конструкцию перехода от высказывания к булевой формуле. Напомним, что в формальное описание составного высказывания входят символы простых высказываний (обыч-но это прописные буквы латинского алфавита), знаки операций Ø, Ù, Ú, →, Å, 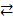и скобки. Заме-ним все прописные буквы латинского алфавита на те же самые, но строчные буквы того же ал-фавита. Будем рассматривать эти буквы как знаки булевых переменных. Само же получившееся (после указанной замены и интерпретации букв как булевых переменных) выражение будем те-перь рассматривать, как формулу в базисе {Ø, Ù, Ú, →, Å, 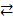} (в смысле точного рекурсивного определения из раздела 2 настоящей главы). Далее именно эти формулу и реализуемую ей буле-ву функцию будем называть формулой и функцией, сопровождающей данное составное выс-казывание. Вместо символов F и T будем использовать символы 0 и 1.

Внимательный читатель может заметить, что формальное выражение составного высказы-вания не является, несмотря на свой формальный характер, строго определённым объектом. В то же время булева формула (над заданным базисом) и реализуемая ей булева функция строго определены рекурсивными процедурами из раздела 2. Поэтому нет гарантии, что для любого составного высказывания его формальное выражение после объявления символов простых выс-казываний булевыми переменными действительно становится корректно определённой форму-лой. Такую гарантию даёт рекурсивная процедура точного определения составных высказыва-ний и соответствующих им выражений, в которые входят только символы простых высказыва-ний, знаки операций и скобки. Такая процедура будет практически совпадать с описанными в разделе 2 процедурами. Мы этого не делаем, не желая загромождать изложение не очень сущес-твенными, но долго описываемыми техническими деталями. Достаточно сказать, что во всех рассматриваемых и упоминаемых ситуациях никаких проблем с однозначным пониманием по-лучающихся выражений именно как булевых формул не возникает.

Ещё раз подчеркнём, что формализация составных высказываний является содержатель-ной операцией (см. раздел 1-3), в то время как сами формулы и функции являются, конечно, формальными, точно определёнными объектами, к которым приложим достаточно сложный и разнообразный математический аппарат. Именно указанное сопоставление формул и функций составным высказываниям и позволяет использовать алгебру логики для их формального ана-лиза. В настоящем пособии затрагивается лишь небольшая часть этого мощного аппарата.

Пример 9.Вернёмся к высказываниям из примеров 1-3,1-4, 1-5, 1-7, 1-9, 1-10, 1-16 и пере-пишем оттуда полученные там формальные выражения для рассмотренных составных высказы-ваний:

(pÙq)®(rÚs), (21а)

((pÙq)®r)ÙØr, (22а)

(((pÙq)®r)ÙØr)®(ØpÚØq), (23а)

(pÚØp)®q, (24а)

(p®q)Ùp, (25а)

((p®q)Ùp)®q, (26а)

(p®r)Ù(r®q))®(p®q). (27а)

После замены прописных букв строчными и интерпретации их как булевых переменных полу-чаем булевы формулы, сопровождающие исходные составные высказывания:

(pÙq)®(rÚs), (21б)

((pÙq)®r)ÙØr, (22б)

(((pÙq)®r)ÙØr)®(ØpÚØq), (23б)

(pÚØp)®q, (24б)

(p®q)Ùp, (25б)

((p®q)Ùp)®q, (26б)

(p®r)Ù(r®q))®(p®q). (27б)

Далее для иллюстрации свойств высказываний мы будем обращаться к этим формулам ■

Пример 10. Рассмотрим ещё раз высказывание из примера 1-4: «Если я – Ваша женщина и Вы – мой мужчина, то я никогда не перестану любить Вас. Я перестала любить Вас». Её сопровождающая формула (22б) равна ((pÙq)®r)ÙØr. Найдём значения этой функции при всех возможных значениях переменных. Для этого построим её таблицу истинности по аналогии с таблицами истинности 6 и 7. В правом столбце таблицы записаны значения этой функции на со-ответствующих наборах. Из таблицы 8 можно сделать следующий вывод. Если все три исход-ных простых высказывания «Я – Ваша женщина», «Вы – мой мужчина» и «Я никогда не пе-рестану любить Вас» ложны, то рассматриваемое составное высказывание истинно. А в слу-чае истинности этих трёх высказываний рассматриваемое составное высказывание ложно.

Таблица 8. Построение таблицы истинности для функции f = ((pÙq)®r)ÙØr.

p	q	r	1) pÙq	2) 1®r	3) Ør	4) 2Ù3

■

Пример 11. Рассмотрим теперь всю «историю» из примера 1-5: «Если я – Ваша женщи-на и Вы – мой мужчина, то я никогда не перестану любить Вас. Я перестала любить Вас. Значит, я – не Ваша женщина или Вы – не мой мужчина». Сопровождающая формула (23б) равна (((pÙq)®r)ÙØr)®(ØpÚØq). Последовательное заполнение соответствующей таблицы ис-тинности 9 показано ниже. Заметим, что часть таблицы 9 скопирована из таблицы 8, поскольку формула (22б) является подформулой формулы (23б).

Таблица 9. Построение таблицы истинности для функции f =(((pÙq)®r)ÙØr)®(ØpÚØq)

p	q	r	1) pÙq	2) 1®r	3) Ør	4) 2Ù3	5) Øp	6) Øq)	7) 5Ú6	8) 4®7

Результат может показаться неожиданным – ведь при всех значениях переменных, т.е. при любых сочетаниях истинности и ложности исходных простых высказываний, данное составное высказывание оказывается истинным! Более того, если построить таблицы истинности для всех сопровождающих формул (21б) – (27б), кроме уже рассмотренной формулы (22) и формулы (25), результат окажется таким же – соответствующие функции тождественно равны 1. Подроб-нее эти вопросы рассматриваются в разделе 3.2 ■

Пример 12. Построим таблицу истинности для формулы (27б), называемой правилом силлогизма. Последовательные шаги показаны в таблице 10.

Таблица 10. Построение таблицы истинности для функции f =((p→r)Ù(r→q))→(p→q)

p	q	r	1) p®r	2) r®q	3) 1Ù2	4) p®q	5) 3®4

■

3.1. Равносильность составных высказываний.Пусть Α = Α(P, Q, ..., Z) и Β= Β(P, Q, ..., Z) - составные высказывания, построенные из высказываний P, Q, ..., Z. Высказывания Α и Β называются равносилъными, что обозначается Α º Β, если сопровождающие их булевы форму-лы равносильны (см. определение равносильности формул в разделе 2.1) Таким образом, уста-новление равносильности высказываний сводится к проверке равносильности формул в базисе {Ø, Ù, Ú, →, Å, 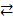}. Последняя задача подробно рассмотрена в разделе 2.2.1.

Обратим особое внимание на разницу между понятиями эквивалентности и равносильнос-ти высказываний. Эквивалентность – это операция над двумя высказываниями; её результатом является новое высказывание, истинностное значение которого определяется таблицей 1-6. Рав-носильность – это логическое значение (истина или ложь), сопоставляемое двум составным высказываниям, зависящим от одних и тех же простых высказываний. Никакая комбинация этих двух высказываний, в отличие от эквивалентности, при этом не определяется.

Составное высказывание называется тождественно истинным (тождественно лож-ным), если сопровождающая его булева функция есть константа 1 (0). Тождественно истинные высказывания называются также тавтологиями. Высказывания с таблицами истинности 9 и 10 являются тавтологиями.

3.2. Логические рассуждения и их значимость.Среди всевозможных составных выска-зываний особую роль играют составные высказывания специального вида, называемые логи-ческими рассуждениями. Он определяется по сопровождающей булевой формуле данного высказывания. Эта формула должна представлять собой импликацию, посылка которой (то, что стоит слева от стрелки) является конъюнкцией отдельных подформул произвольного вида (которым в исходном высказывании соответствуют предположения, правила, законы, наблюдения и т.д.). Эти отдельные подформулы называются предпосылками логического рассуждения. Подформула произвольного вида, являющаяся заключением импликации (то, что стоит справа от стрелки) называется выводом логического рассуждения. Таким образом, логическое рассуждение можно условно изобразить в следующем виде:

( P₁ Ù P₂ Ù......Ù P_k ) ® C

↑ ↑ ↑ ↑ ↑ ↑ ↑ ↑ ↑ (28)

(предпосылка 1 и предпосылка 2 и.......и предпосылка k) влекут вывод

Как предпосылки, так и вывод могут быть достаточно сложными формулами, построенными по составными высказываниями ■

Пример 13. Формулы (21б), (23б), (24б), (26б), (27б) сопровождают высказывания, кото-рые в силу определения являются логическими рассуждениями. Приведём все эти высказыва-ния, для бóльшей наглядности, вместе:

1. «Если будет солнечно и температура превысит 25⁰, я приеду поездом или автомо-билем»

2. «Если я – Ваша женщина и Вы – мой мужчина, то я никогда не перестану любить Вас. Я перестала любить Вас. Значит, я – не Ваша женщина или Вы – не мой мужчина»

3. «Женат я или не женат, я счастлив»

4. «Если пол грязный, то я должен вымыть его. Пол грязный. Поэтому я должен вы-мыть его»

5. «Все мужчины созданы равными. Все люди, созданные равными, являются женщи-нами. Поэтому все мужчины являются женщинами»■

Пример 14. Рассмотрим высказывание: «Если Вы хотите улучшить свою сердечно-со-судистую систему, то стоит кататься на беговых (не горных) лыжах. Вы катаетесь на беговых лыжах. Значит, Вы хотите улучшить свою сердечно-сосудистую систему». В этом составном высказывании выделяются два простых высказывания

P = «Вы хотите улучшить свою сердечно-сосудистую систему»,

Q = «Вы катаетесь на беговых лыжах».

Сопровождающая функция равна ((p®q)Ùq)®p. Эта функция является импликацией, а её по-сылка является конъюнкцией двух предпосылок: p®q и q. Таким образом, исходное высказыва-ние является логическим рассуждением ■

Пример 15.Вернёмся к высказыванию из примера 10: «Если я – Ваша женщина и Вы – мой мужчина, то я никогда не перестану любить Вас. Я перестала любить Вас». Её сопровождающая формула (22б) равна ((pÙq)®r)ÙØr. Эта формула не представлена в виде (28), и, следовательно, это высказывание не является логическим рассуждением ■

Важным понятием является понятие значимости логического рассуждения. Рассуждение называется значимым, если из истинности всех предпосылок обязательно следует истинность вывода. Проверка значимости осуществляется следующим образом.