Уравнения электромагнитного переходного процесса синхронной машины

Общие сведения об электромагнитных переходных процессах

Основными причинами возникновения электромагнитных переходных процессов являются:

· Включение и отключение двигателей и других приемников электрической энергии;

· Короткое замыкание в электрической системе, автоматическое повторное включение линии на сохранившееся короткое замыкание;

· Возникновение местной несимметрии в системе;

· Действие форсировки возбуждения синхронных машин, их развозбуждение;

· Несинхронное включение синхронных машин.

Коротким замыканием называют всякое, не предусмотренное нормальными условиями работы, замыкание между фазами, а в системах с заземленными нейтралями – замыкание одной или нескольких фаз на землю.

В трехфазных системах с заземленной нейтралью различают следующие основные виды коротких замыканий в одной точке:

· Трехфазное короткое замыкание – К⁽³⁾;

· Двухфазное короткое замыкание – К⁽²⁾;

· Однофазное короткое замыкание – К⁽¹⁾;

· Двухфазное короткое замыкание на землю – К^(1,1).

Симметричным называют такое короткое замыкание, когда при нем все фазы остаются в одинаковых условиях, иначе короткое замыкание называют несимметричным.

Следствиями действия тока короткого замыкания являются:

· Дополнительный нагрев токоведущих элементов и проводников выше допустимого;

· Возникновение больших механических усилий между проводниками;

· Снижение напряжения, приводящее к ухудшению эффективности работы потребителей, авариям на электростанциях и подстанциях;

· Нарушение работы линий связи и сигнализации, за счет наведения дополнительных магнитных потоков;

· Нарушение устойчивости электрических систем.

Токи короткого замыкания с учетом действия устройств релейной защиты обычно существуют непродолжительное время, но их приходится учитывать и тщательно рассчитывать ввиду вышеуказанных последствий. По режиму короткого замыкания должны проверяться

1) В электроустановках выше 1 кВ:

а) электрические аппараты, токопроводы, кабели и другие проводники, а также опорные конструкции для них;

б) воздушные линии при ударном токе короткого замыкания 50 кА и более для предупреждения схлестывания проводов при динамическом действии токов короткого замыкания.

2) В электроустановках до 1 кВ – распределительные щиты, токопроводы и силовые шкафы.

Аппараты, которые предназначены для отключения токов короткого замыкания, должны обладать способностью производить эти операции при всех возможных токах короткого замыкания.

Уравнения электромагнитного переходного процесса синхронной машины

Переходный процесс в электрической машине любого типа может быть описан системой дифференциальных уравнений в той или иной системе координат. Выбор системы координат определяется конкретными условиями решаемой задачи. Дифференциальные уравнения равновесия ЭДС и падений напряжений в каждой из обмоток статора (А, В, С) и ротора (f):

U_А=-∂Ψ_А/∂t-R_А∙i_A ;

U_В=-∂Ψ_В/∂t-R_В∙i_В ;

U_С=-∂Ψ_С/∂t-R_С∙i_С ;

U_f=∂Ψ_f/∂t+R_f∙i_f ,

где R_А, R_В, R_С, R_f – активные сопротивления контуров фаз А, В, С и обмотки возбуждения; Ψ_А, Ψ_В, Ψ_С, Ψ_f - результирующие потокосцепления контуров фаз А, В, С и обмотки возбуждения.

Входящее в эту систему потокосцепление обмотки фазы А выражается уравнением:

Ψ_А=L_Аi_А+M_АВi_В+M_АСi_С+M_Аfi_f ,

где L_А – коэффициент самоиндукции обмотки фазы А; M_АВ - коэффициент взаимоиндукции обмоток фаз А и В; M_АС - коэффициент взаимоиндукции обмоток фаз А и В; M_Аf - коэффициент взаимоиндукции обмотки фазы А и обмотки возбуждения.

Аналогичными уравнениями выражаются потокосцепления для обмоток других фаз. Закон изменения взаимных индуктивностей между обмоткой возбуждения и каждой фазной обмоткой статора выражается синусоидальной функцией. Систему дифференциальных уравнений с переменными коэффициентами решить очень сложно. Для её решения существуют несколько способов. Известно, что мгновенные значения фазных величин (U, Ψ, i) можно получить как проекции фазных векторов на неподвижную ось времени или как проекции обобщенного вектора на неподвижные магнитные оси фаз. Обобщенный вектор в общем случае может характеризовать фазные величины, изменяющиеся во времени по произвольному закону. Возможность представления трехфазной системы векторов обобщенным вектором существенно упрощает выражение связи между статором и ротором, что позволяет в дифференциальных уравнениях переходного процесса освободится от переменных коэффициентов. Представление фазных величин f_А, f_В, f_С через обобщенный вектор возможно при условии:

f_А+f_B+f_C=0.

Если сумма фазных переменных не равна нулю, то её целесообразно выразить через новое переменное f₀ : f_А+f_B+f_C=3f₀. Нулевая составляющая во всех фазах одинакова и тождественна составляющей нулевой последовательности метода симметричных составляющих. Фазные переменные, выраженные через обобщенный вектор:

f_А=f∙cosα;

f_В=f∙cos(α-2π/3);

f_С=f∙cos(α+2π/3),

где α - угол между векторами f_А и f.

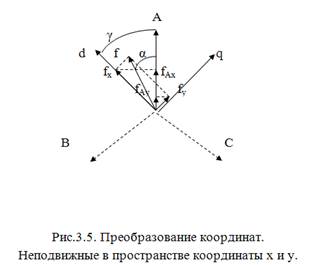
Обобщенный вектор можно выразить и в двухосной системе координат. В качестве последней удобно выбрать декартовые ортогональные координаты. Преобразование координат соответствует замене переменных. Проекции вектора f (рис.3.5.) на оси х и у:

f_Х=f∙cos(θ-α);

f_У=f∙sin(θ-α),

где θ - угол между магнитной осью фазы А и осью Х.

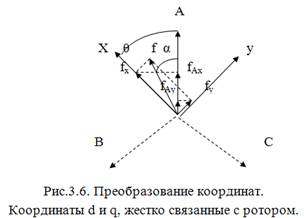
Применение новой системы координат сокращает переменные коэффициенты. Значительные упрощения можно достичь, используя декартову систему координат, жестко связанную с ротором синхронной машины. Эту систему координат сокращенно обозначают и называют d, q и 0 (рис.3.6). Поскольку фазные обмотки синхронной машины, расположенные в осях d, q, неподвижны относительно ротора, все индуктивности такой машины постоянны. Фазные переменные в системе координат d, q и 0:

f_А=f_dcosγ+f_qsinγ+f₀;

f_В=f_dcos(γ - 2π/3)+f_qsin(γ - 2π/3)+f₀;

f_С=f_dcos(γ+2π/3)+f_qsin(γ+2π/3)+f₀,

где γ=ω_сt+γ₀ – угол, характеризующий положение ротора в пространстве; ω_с - синхронная угловая скорость, γ₀- начальный уг

Фазные переменные напряжения, тока в системе координат d, q и 0:

U_А=U_d∙cosγ+U_q∙sinγ+U₀;

i_А=i_d∙cos(γ - 2π/3)+i_q∙sin(γ - 2π/3)+i₀;

Ψ_А=Ψ_d∙cos(γ+2π/3)+Ψ_q∙sin(γ+2π/3)+Ψ₀.

Подставляя фазные переменные в дифференциальное уравнение равновесия обмотки фазы А получим уравнения Парка-Горева:

U_d=-∂Ψ_d/∂t-Ψ_q∙∂γ/∂t-R∙i_d ;

U_q=-∂Ψ_q/∂t-Ψ_d∙∂γ/∂t-R∙i_q ;

U₀=-∂Ψ₀/∂t-R∙i₀ ,

где ∂Ψ_d/∂, ∂Ψ_q/∂t, ∂Ψ₀/∂ – ЭДС трансформации, которые вызываются изменением величин потокосцеплений; Ψ_q∙∂γ/∂ и Ψ_d∙∂γ/∂t – ЭДС вращения (скольжения).

70.

71. Переходные э. д. с. и реактивности синхронной ма­шины.

Обратимся к синхронной явнополюсной машине без демпферных (успокоительных) обмоток. При КЗ в статорной цепи возникает переходный процесс, приводящий к изменению токов и напряжений предшествующего режима. Выясним, какими ЭДС и реактивностями можно характеризовать синхронную машину в начальный момент переходного процесса с целью расчета периодической составляющей тока КЗ для .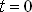

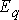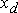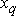Постановка задачи обусловлена тем, что синхронная ЭДС ( ), характеризующая машину в установившемся режиме, в момент КЗ скачкообразно изменяется. В силу этого она неизвестна и неприемлема для расчета переходного режима, равным образом как и и , связанные с .

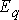Для решения поставленной задачи обратимся к балансу магнитных потоков в продольной оси ( 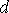) синхронной машины для нормального нагрузочного режима (рис. 4.4, а). В указанной оси взаимодействуют две магнитосвязанные обмотки: обмотка возбуждения и обмотка статора.

В режиме холостого хода ток обмотки возбуждения 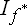создает магнитный поток 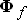, состоящий из потока рассеяния ротора 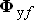и полезного потока :

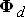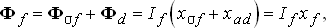(4.5)

где: 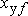– реактивность рассеяния обмотки возбуждения;

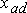– индуктивное сопротивление реакции статора по оси ;

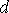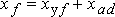– полная индуктивность обмотки возбуждения.

Полезный поток 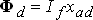при вращении ротора обуславливает в статоре синхронную ЭДС, которые в системе относительных единиц одинаковы:

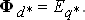В ненасыщенной машине поток 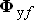составляет некоторую постоянную долю потока 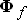, которая характеризуется коэффициентом рассеяния обмотки возбуждения

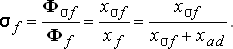(4.6)

В нагрузочном режиме продольная составляющая тока статора 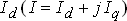создает поток реакции статора 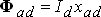, который пронизывает обмотку возбуждения. В соответствии с этим полное потокосцепление обмотки возбуждения в нагрузочном режиме определяется выражением:

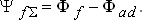(4.7)

Согласно принципа Ленца при внезапном изменении режима магнитосвязанных контуров результирующее потокосцепление обмотки возбуждения 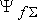остается неизменным. Физически это означает, что в начальный момент КЗ потоки и можно представить как их значения в нормальном режиме ( 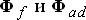) плюс соответствующие им приращения 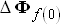и 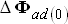. Однако приращения потоков компенсируют друг друга, т.е.

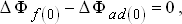оставляя неизменным значение 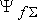, согласно выражения (4.7).

Для решения ранее сформулированной задачи используем неизменность 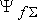. Зная коэффициент рассеяния 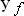, выделим ту часть 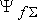, которая связана со статором

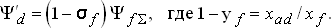(4.8)

Именно это потокосцепление 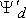и обусловленная им ЭДС в обмотке статора 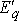сохраняют в начальный момент переходного процесса свое предшествующее значение.

Придадим выражению (4.8) более наглядный вид:

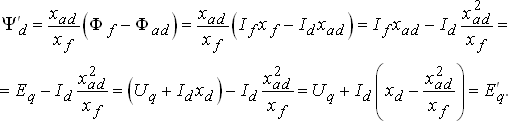
В окончательной форме поперечная переходная ЭДС 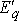запишется так:

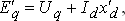(4.9)

где:

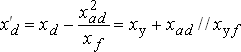(4.10)

– продольная переходная реактивность; приводиться в паспортных данных машины;

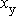– реактивность рассеяния статорной обмотки.

Начальное значение 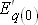определяется выражением (4.9) по параметрам 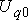и 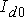, с которыми работала машина до нарушения режима.