Будь-яка впорядкована множина, яка складається з n елементів, називається перестановкою з n елементів і позначається Рn

Таким чином, перестановки з n елементів відрізняються між собою лише порядком елементів.

Два елементи а і b можна упорядкувати двома способами: ab і bа. Це дві перестановки з елементів a і b. Отже, Р₂ = 2.

Щоб утворити перестановки з трьох елементів а, b, с можна третій елемент с помістити попереду пари ab, посередині пари аb та вкінці пари ab:

cab, acb, abc.

Точно так із пари bа можна одержати:

cba, bca, bac.

Отже, для трьох елементів існує 2 · 3 = 6 способів розташу­вання по порядку, число перестановок з трьох елементів дорів­нює 6. P₃ = 2 · 3 = 6.

Нехай маємо k елементів, із яких складені всі можливі Р_k перестановки. Візьмемо одну із них: а₁а₂а₃...а_k. Добавимо ще один (k + 1)-й елемент. Його можна помістити:

1) перед першим елементом а₁;

2) перед другим елементом а₂;

3) перед третім елементом a₃;

……………………………………

k) перед k-им елементом а_k;

(k + 1) в кінці всіх елементів, тобто, всього k + 1 способом.

Отже, кількість перестановок із k + 1 елементів в (k + 1) раз більша, ніж число перестановок із k елементів, тобто,

.

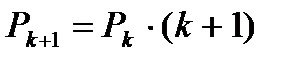Отже,

P₁ ⁼ 1;

P₂ = P₁ · 2 = 1 · 2 = 2;

P₃ = P₂ · 3 = 1 · 2 · 3 = 6;

P₄ = Рз · 4 = 1 · 2 · 3 · 4 = 24;

P₅ = P₄ · 5 = 1 ∙ 2 ∙ 3 ∙ 4 ∙ 5 = 120;

………………………………

P_k = P_k-1 · k = 1-2· 3 ·... · k;

P_k+1=P_k · (k+1) = 1 · 2 · 3 ·...· k · (k+l).

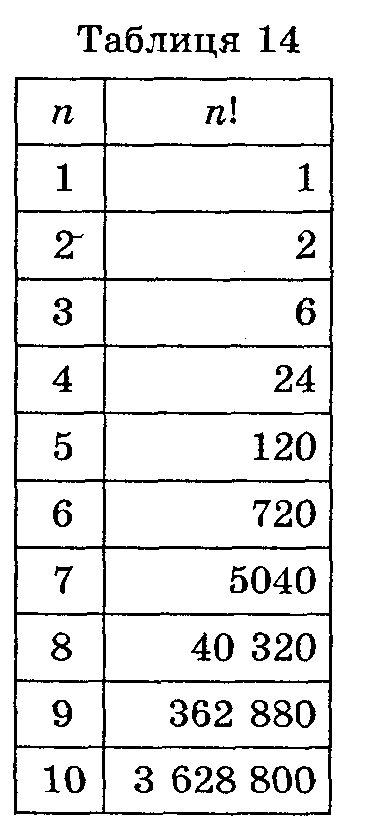
Добуток натуральних чисел від 1 до даного натурального числа η називається факторіалом числа n і позначається n! В таблиці наведено значення факторіала для значень п від 1 до 10.

Число перестановок з n елементів дорівнює добутку всіх натуральних чисел від 1 до п, тоб­то п! (читають: єн факторіалів).

Задача. Скількома способами можна розставити на майданчику 6 волейболістів?

Розв'язання

P₆ = 6! =l · 2 · 3 · 4 · 5 · 6 = 720.