Многофакторный регрессионный анализ
ОДНОФАКТОРНЫЙ РЕГРЕССИОННЫЙ АНАЛИЗ
С ПРИМЕНЕНИЕМ ИНСТРУМЕНТА РЕГРЕССИИ
Для проведения регрессионного анализа зависимости снижения себестоимости от изменения удельного веса рабочих в составе ППП. В меню Сервис выбираем Анализ данных и указываем инструмент анализа Регрессия. После нажатия ОК в диалоговом окне Регрессия указываем входной интервал Y и входной интервал X, а также параметры вывода, остатки, нормальную вероятность. Аналогично производится парный регрессионный анализ по второй переменной - зависимости индекса снижения себестоимости от уровня непроизводственных расходов.
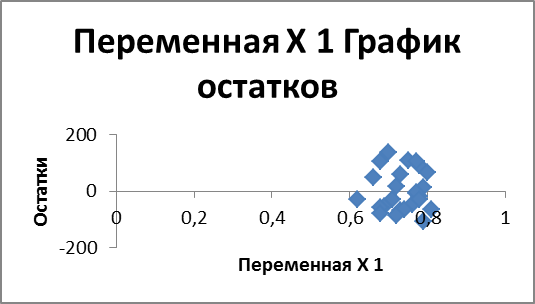
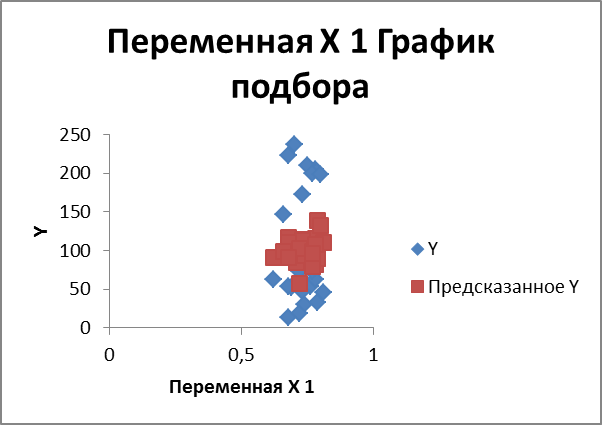
- себестоимость и удельный вес рабочих
ВЫВОД ИТОГОВ
| Регрессионная статистика | |
| Множественный R | 0,052071515 |
| R-квадрат | 0,002711443 |
| Нормированный R-квадрат | -0,040648929 |
| Стандартная ошибка | 74,00339097 |
| Наблюдения |
Множественный R в пределах 0,5-0,7 свидетельствует о заметной связи признаков;
R-квадрат- коэффициент детерминации характеризует долю вариации результативного признака у, объясняемую регрессией и фактором х, в общей вариации у – от 0 до 1, показывает, что 2 выбранных фактора на 0,27% обусл. У, 99,73%-не учтено. Стандартная ошибка – для оценки качества модели.
Дисперсионный анализ
| df-степени свободы |
| число факторов-2 |
| F оценка качества модели сравниваем с табличным для уровня значимости альфа 0,05 | |
| по приложению А Fтабл = 3,44 | Fрасч=0,06 меньше ф табл, значит уравнение не значимо |
Фактическое значение меньше табличного, значит нет оснований отвергать основную гипотезу, то есть параметр регрессии не значимо отличается от нуля при уровне значимости 0,05
ВЫВОД ОСТАТКА
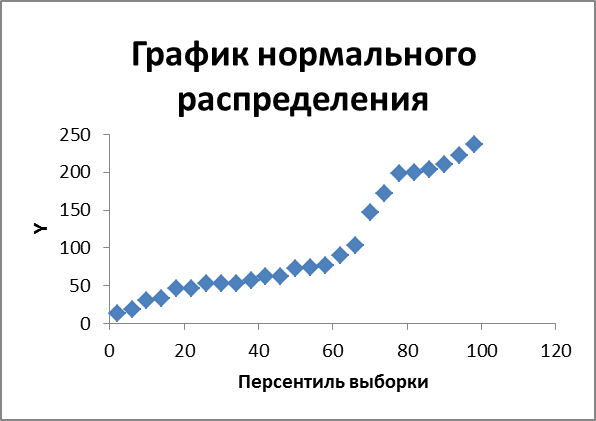
ВЫВОД ВЕРОЯТНОСТИ
| Персентиль | Y |
| 13,6 | |
| 18,1 | |
| 30,1 | |
| 32,3 | |
| 46,3 | |
| 46,6 | |
| 52,6 | |
| 53,1 | |
| 53,2 | |
| 56,5 | |
| 62,5 | |
| 73,01 | |
| 73,3 | |
| 76,6 | |
| 89,8 | |
| 103,5 | |
| 146,4 | |
| 172,1 | |
| 198,1 | |
| 199,6 | |
| 204,2 | |
| 209,6 | |
| 222,6 | |
| 236,7 |
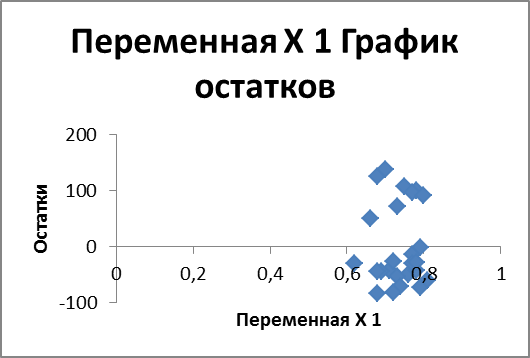
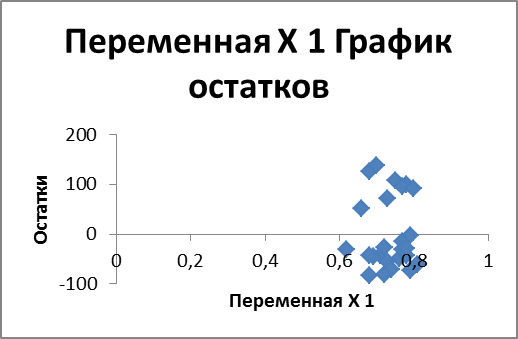
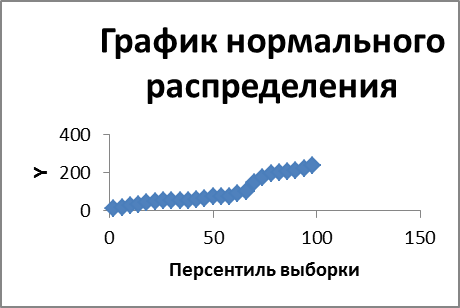
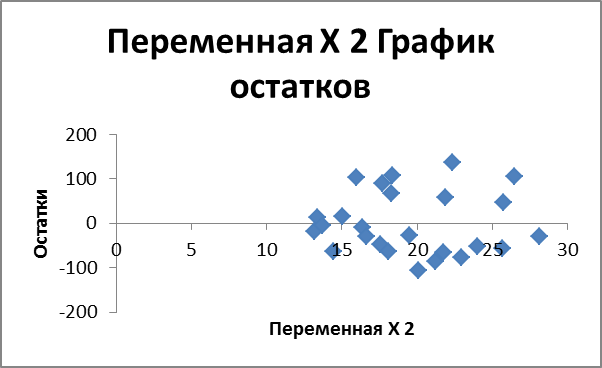
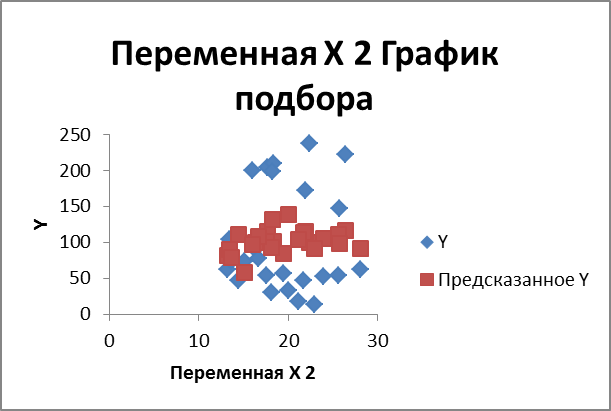
- себестоимость и расходы
ВЫВОД ИТОГОВ
| Регрессионная статистика | |
| Множественный R | 0,071828488 |
| R-квадрат | 0,005159332 |
| Нормированный R-квадрат | -0,03809461 |
| Стандартная ошибка | 73,91251287 |
| Наблюдения |
Множественный R в пределах 0,7-0,9 свидетельствует о тесной связи признаков;
R-квадрат- коэффициент детерминации характеризует долю вариации результативного признака у, объясняемую регрессией и фактором х, в общей вариации у – от 0 до 1, показывает, что 2 выбранных фактора на 0,5% обусл. У, 99,5%-не учтено. Стандартная ошибка – для оценки качества модели.
Дисперсионный анализ
| df-степени свободы |
| число факторов-2 |
| F оценка качества модели сравниваем с табличным для уровня значимости альфа 0,05 | |
| по приложению А Fтабл = 3,44 | Fрасч=0,1 меньше ф табл, значит уравнение не значимо |
Фактическое значение меньше табличного, значит нет оснований отвергать основную гипотезу, то есть параметр регрессии не значимо отличается от нуля при уровне значимости 0,05
ВЫВОД ОСТАТКА
ВЫВОД ВЕРОЯТНОСТИ
| Персентиль | Y |
| 13,6 | |
| 18,1 | |
| 30,1 | |
| 32,3 | |
| 46,3 | |
| 46,6 | |
| 52,6 | |
| 53,1 | |
| 53,2 | |
| 56,5 | |
| 62,5 | |
| 73,01 | |
| 73,3 | |
| 76,6 | |
| 89,8 | |
| 103,5 | |
| 146,4 | |
| 172,1 | |
| 198,1 | |
| 199,6 | |
| 204,2 | |
| 209,6 | |
| 222,6 | |
| 236,7 |

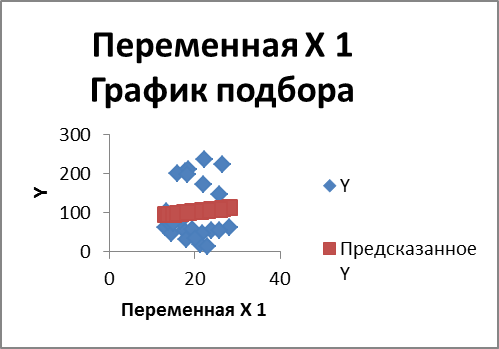
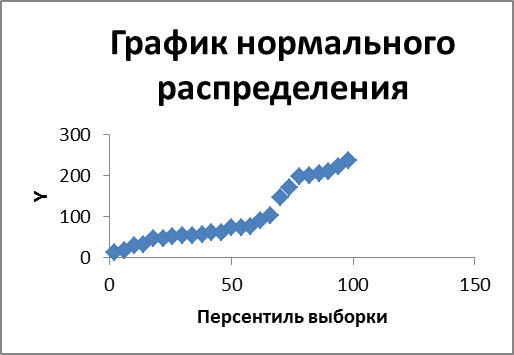
МНОГОФАКТОРНЫЙ РЕГРЕССИОННЫЙ АНАЛИЗ
Эта операция производится с помощью инструмента анализа данных Регрессия. Она аналогична расчету параметров парной линейной регрессии. описанной выше, только в отличие от парной регрессии в диалоговом окне при заполнении параметра входной интервал X следует указать не один столбец, а все столбцы, содержащие значения факторных признаков. Результаты анализа представлены в приложении Д.
- себестоимость, удельный вес рабочих, затраты
ВЫВОД ИТОГОВ
| Регрессионная статистика | |
| Множественный R | 0,232355909 |
| R-квадрат | 0,053989268 |
| Нормированный R-квадрат | -0,032011707 |
| Стандартная ошибка | 73,69564283 |
| Наблюдения |
Множественный R в пределах 0,1-0,3 свидетельствует о слабой связи признаков;
R-квадрат- коэффициент детерминации характеризует долю вариации результативного признака у, объясняемую регрессией и фактором х, в общей вариации у – от 0 до 1, показывает, что 2 выбранных фактора на 0,5% обусл. У, 99,5%-не учтено. Стандартная ошибка – для оценки качества модели.
Дисперсионный анализ
| df-степени свободы |
| число факторов-2 |
| F оценка качества модели сравниваем с табличным для уровня значимости альфа 0,05 | |
| по приложению А Fтабл = 3,44 | Fрасч=0,6 меньше ф табл, значит уравнение не значимо |
Фактическое значение меньше табличного, значит нет оснований отвергать основную гипотезу, то есть параметр регрессии не значимо отличается от нуля при уровне значимости 0,05
ВЫВОД ОСТАТКА
ВЫВОД ВЕРОЯТНОСТИ
| Персентиль | Y |
| 13,6 | |
| 18,1 | |
| 30,1 | |
| 32,3 | |
| 46,3 | |
| 46,6 | |
| 52,6 | |
| 53,1 | |
| 53,2 | |
| 56,5 | |
| 62,5 | |
| 73,01 | |
| 73,3 | |
| 76,6 | |
| 89,8 | |
| 103,5 | |
| 146,4 | |
| 172,1 | |
| 198,1 | |
| 199,6 | |
| 204,2 | |
| 209,6 | |
| 222,6 | |
| 236,7 |