Процесс пассивного торможения описывается дифференциальным уравнением

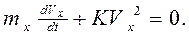(2.7)

Он имеет два периода. Прохождение команды t', от момента подачи команды "Стоп" до прекращения подачи топлива на главный двигатель, (и обычно его принимают равным 10 с). Собственно пассивное торможение t'', от начальной скорости V_o до конечной скорости V_к, которую принимают равной 0.2 V₀ или скорости потери управляемости, что наступит раньше.

Решение уравнения (2.7) относительно пути, времени и скорости позволяет получить следующие выражения. Значение пути I периода равно

S^I = 0.514·V₀·t^I, (2.8)

где V₀ –начальная скорость в узлах; t^I – время I периода, которое в системах с дистанционным автоматизированным управлением (ДАУ) составляет около 5 с, в обычных двигателях можно принять равным 10 с.

Значение времени и пути II периода равно

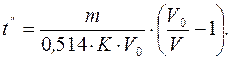(2.9)

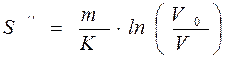. (2.10)

где, К - коэффициента общего сопротивления

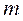- масса судна.

Время и путь пассивного торможения будут равны

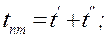
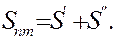(2.11)

Информация о пассивном торможении используется при снижении скорости перед началом маневрирования, в случае отказа двигателя или как составная часть активного торможения.

Активное торможение.

Активным торможением называется процесс уменьшения скорости движения судна за счет упора винта, работающего на задний ход.

Процессактивного торможения описывается дифференциальным уравнением

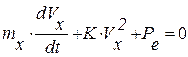. (2.12)

В зависимости от соотношения скорости хода перед началом снижения V_o и скорости уверенного реверсирования V_pев (т.е. скорости при которой главный двигатель уверенно запускается на задний ход), общее время и путь активного торможения будут рассчитываться различным образом.

Полное время и путь в полном цикле активного торможения

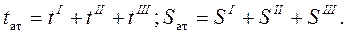(2.13)

При V_o > V_peв значение пути первого периода рассчитывают как обычно S' = V_o • t'. Во время второго периода будет происходить пассивное торможение до тех пор, пока скорость не упадет до V_рeв, а расчет пути произведем по формуле (7), подставляя вместо V_к = V_peв.

При V_o < V_рев расчет пути первого периода производится аналогично предыдущему случаю, а время второго периода определяется техническими характеристиками главного двигателя и равно времени запуска двигателя на задний ход. Для ДВС, в соответствии с правилами технической эксплуатации, оно равно t'' =15 секунд. С учетом этого путь второго периода рассчитывают по формуле S" = V_o× t".

Графики зависимости V(t) и S(t) (рисунок 5) достаточно подробно описывают процесс маневрирования, однако их требуется большое количество для полной характеристики динамики судна, как объекта управления (около 18 листов по 5 характеристик на каждом).

Выборка данных о времени и пути торможения на мостике практически исключена, поскольку сам процесс их получения занимает достаточно много времени, которое соизмеримо со временем маневрирования и необходимые данные запаздывают к моменту принятия решения. Поэтому такой вид представления рекомендуется при проведении научно-исследовательских работ и в учебном процессе в морских учебных заведениях.

Разгон.

Разгон представляет собой процесс увеличения скорости от низшей ступени к высшей. Особым случаем такого маневра является разгон из неподвижного состояния и разгон с переложенным рулем.

Процессразгона описывается дифференциальным уравнением

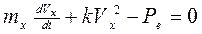. (2.14)

Для упрощения решения дифференциального уравнения (26) при переходных режимах необходимо ввести дополнительное допущение, что назначенная сила упора движителя устанавливается мгновенно, в момент подачи команды, и равна новому режиму движения. Такое допущение можно сделать потому, что переходные процессы в двигателях происходят значительно быстрее, чем изменение скорости хода.

По окончании разгона, когда судно будет двигаться с установившейся скоростью V_ycт, сила инерции равна нулю, и уравнение (26) принимает вид

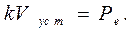(2.15)

Подставив (27) в (26) получим дифференциальное уравнение разгона

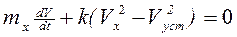. (2.16)

Вид решения уравнения (28) зависит от того, из какого начального состоя 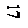ния производится разгон - из неподвижного состояния или от меньшей

скорости к большей. В первом случае после разделения переменных в уравнении (28) и интегрирования в пределах от 0 до V_x получим выражения для расчета пути и времени разгона

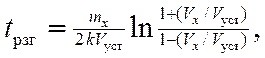(2.17)

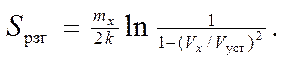(2.18)

Полученные формулы позволяют получить время и путь разгона судна из неподвижного состояния до заданной установившейся скорости.

Процессразгона от произвольной скорости V₁ до значения V_уст описывается дифференциальным уравнением, с пределами интегрирования от V₁ до V_yст. Тогда формулы для расчета пути и времени разгона принимают вид

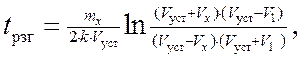(2.19)

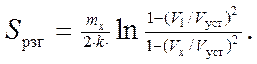(2.20)

С учетом того, что процесс разгона от скорости V₁ до V_ycт также длится продолжительное время, выражения для расчета конечного пути и времени разгона до 0.95 V_уст упростятся и принимают вид

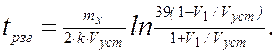(2.21)

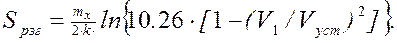(2.22)

Время разгона от ПП_м до ПП является технической характеристикой двигателя судна. В зависимости от его типа продолжительность такого периода составляет от 25 до 45 мин., а для крупнотоннажных судов до 2-х часов. Поэтому при подсчете пути разгона скорость можно считать линейно нарастающей от ПП_м до ПП, а путь рассчитать по средней ее величине.

Подтормаживание.

Подтормаживанием называется процесс уменьшения скорости от высшей ступени движения к низшей.

При этом процесс движения судна описывается дифференциальным уравнением (28), с интегрированием от текущей скорости V₁ до V_уст. В результате получим формулы для расчета времени t_птр и пути S_птр подтормаживания

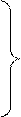
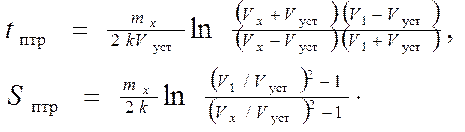(2.23)

Учитывая, что процесс подтормаживания занимает продолжительное время, его можно считать законченным когда значение текущей скорости V_x равно 1.05 V_ycт. Подставив его значение в формулы (37), получим формулы для расчета конечных значений пути и времени подтормаживания

(24)     (25)

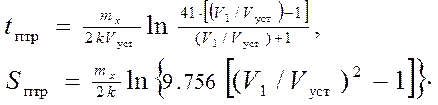
При расчете времени подтормаживания из ходового режима необходимо учитывать время перевода главной силовой установки в маневренный режим. По приведенным формулам можно рассчитать время и путь, проходимый судном за период подтормаживания от ПП_м до ПСМ. Перевод до режима «Стоп» можно рассчитать по формулам пассивного торможения и считать его частным случаем подтормаживания.

Вопросы для самоконтроля

1. Судно как объект управления. Составные части управляемой системы. Замкнутая система управления. Координаты состояния судна в данный момент.

2. Группы сил, действующие на судно: дать определения, перечислить основные.

3. Инерционные и неинерционные силы и моменты.

4. Подвижная система координат. Положительное направление осей и положительный отсчет углов (перекладки руля, дрейфа).

5. Система дифференциальных уравнений движения.

6. Классификация маневренных характеристик.

7. Информация капитану о маневренных элементах судна. Представление инерционно-тормозных характеристик и характеристик поворотливости.

8. Общие сведения об инерционно-тормозных свойствах судна.

9. Дифференциальное уравнение изменение скорости прямолинейного движения судна.

10. Присоединенная масса воды при движении по оси Х.

11. Сила сопротивления воды при движении судна.

12. Сила упора гребного винта.

13. Тормозные характеристики судна. Пассивное и активное торможение.

14. Реверсирование ДВС – ВФШ.

15. Реверсирование ТЗА – ВФШ.

16. Реверсирование ГЭД – ВФШ.

17. Реверсирование ВРШ.

18. Три периода процесса торможения.

19. Формула расчета пути и времени судна при активном торможении.

20. Формула расчета пути и времени судна при пассивном торможении.

21. Представление тормозных характеристик: графики V и S от времени, графики ИМО, графики зависимости V(t) и S(t)/.

22. Формулы для расчета разгона и подтормаживания судна.

23. Порядок расчета пути и времени разгона и подтормаживания судна.

Литература для самостоятельного изучения, имеющаяся в технической библиотеке ИФ ОНМА:

1. Яркин П.И. Управление судном. (Учебное пособие). ОНМА. Одесса, 2007.

2. Мальцев А.С. Методические указания по выполнению курсовой работы на тему «Определение маневренных характеристик судна». ОНМА, Одесса, 2007.

3. Справочник капитана дальнего плавания // Под ред. Г.Г. Ермолаева. –М.: «Транспорт», 1988.

4. В.И. Снопков В.И. Управление судном. – М.: «Транспорт», 1991.