Логарифмические частотные характеристики

Построение амплитудно-фазовой, амплитудной и фазовой частотных характеристик производится по точкам, поэтому оно требует кропотливых расчетов.

Необходимость сокращения трудоемкости построения частотных характеристик привела к использованию в практике расчета САУ логарифмических частотных характеристик (ЛЧХ). Такое построение было предложено американским радиоинженером Хендриком Боде, поэтому ЛЧХ еще иногда называют диаграммами Боде или характеристиками усиления. Получаемые при этом графические изображения называются: для амплитуды - логарифмическая амплитудно-частотная характеристика (ЛАХ), для фазы - логарифмическая фазочастотная характеристика (ЛФХ). При построении графиков ЛЧХ и ЛФХ по оси абсцисс откладывается логарифм комплексной частоты ϖ в линейном масштабе в результате чего в отношении lg ϖ шкала вдоль абсцисс получается равномерной. Однако разметка оси абсцисс производится обычно не по значениям lg ϖ, а по соответствующим им значениям самой частоты, вследствие чего в отношении ϖ шкала получается равномерной (рисунок 2.15,а).

Терминология, которой пользуются при построении ЛЧХ, заимствована из акустики. Поэтому говорят, что частоты ϖ₁ и ϖ₂ отличаются друг от друга на октаву, если 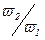=2 и на декаду, если 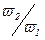=10.

При построении АЧХ по оси ординат откладывается отношение выходной и входной амплитуд, при переходе же к ЛАХ используют единицу отношения мощностей - бел.

Мощности Р₁ и Р₂ отличаются друг от друга на один бел, если 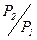=10 или 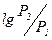=1. Это сравнительно большая единица измерения. В практике получила распространение более мелкая единица - децибел, то есть

1 дб = 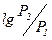= 0,1 бела

или

1 дб = 10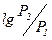

Известно, что мощности пропорциональны квадрату амплитуд тока, напряжения и др.

Если перейти от отношения мощностей к отношению амплитуд, то для децибела получим следующее выражение

1 дб = 20 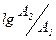= 20 lg A(v)

Прологарифмируем выражение частотной передаточной функции (2.75):

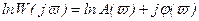, (2.90)

Из данного выражения следует, что логарифм частотной передаточной функции представляет собой комплексную функцию, вещественной частью которой является логарифм АЧХ, а мнимой - ФЧХ.

В практических расчетах ЛАХ и АФХ строят отдельно.

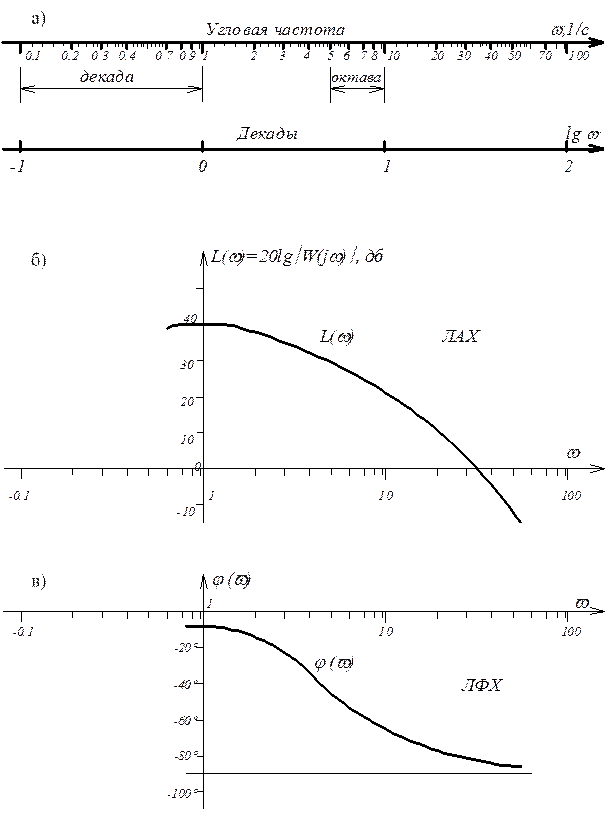
Рисунок 2.15 Логарифмические характеристики

При построении ЛАХ на графике откладывается не ln A(ϖ), а пропорциональная этому выражению величина.

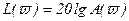, (2.91)

Формула (2.91) дает характеристику в децибелах. Масштаб по оси ординат используется равномерный, так как по ней откладывается модуль в децибелах.

Ось ординат может пересекать ось абсцисс в любом месте. Обычно ее размещают таким образом, чтобы показать весь ход построения ЛАХ (рисунок 2.15, б).

При построении ЛФХ по оси абсцисс так же используется логарифмический масштаб частоты, а по оси ординат откладывается фаза в линейном масштабе (рисунок 2.15, в).

В отличие от обычных частотных характеристик, ЛАХ в большинстве случаев может быть построена практически без вычислений. Это является главным достоинством логарифмических частотных характеристик.

Кроме того, технические требования, предъявляемые к системе регулирования, часто содержат указание скорости реакции, времени установления, которые могут быть связаны с частотной характеристикой. Поэтому ЛАХ и ЛФХ могут быть непосредственно использованы для синтеза желаемой характеристики.