Теоремы сложения и умножения вероятностей

КРАТКИЙ КУРС ЛЕКЦИЙ ПО ДИСЦИПЛИНЕ

«Элементы высшей математики»

Элементы теории вероятностей

Вопросы для изучения:

Случайные события.

Вероятность события.

Теоремы сложения и умножения вероятностей.

Формула полной вероятности и формула Байеса.

5. Случайные величины.

6. Распределение Пуассона.

7. Функция распределения вероятностей случайной величины.

8. Плотность распределения вероятностей случайной величины.

9. Числовые характеристики непрерывных случайных величин.

Случайные события

Теория вероятностей занимается изучением закономерностей случайных событий и случайных величин при массовом их появлении.

Под случайным событием в теории вероятностей понимается событие, которое в результате опыта (испытания) может произойти или не произойти.

Событие называется достоверным, если оно обязательно произойдет в результате испытания, и невозможным, если оно не может произойти в результате испытания. Так при подбрасывании монеты достоверным является появление орла или решки и невозможным – появление кирпича.

События называются несовместными, если они не могут наблюдаться в одном и том же испытании одновременно. Так при бросании монеты появление орла или решки – несовместные события.

Суммой событий называется событие, состоящее в появлении хотя бы одного из этих событий.

Произведением событий называется событие, состоящее в одновременном появлении всех этих событий.

События являются равновозможными, если по условиям испытания нельзя считать, что одно из них может быть более возможным, чем другое.

Вероятность события

Количественной мерой возможности появления события является вероятность. Наиболее широкое распространение имеют два определения вероятности события: классическое и статистическое.

Классическое определение вероятности связано с понятием элементарного события, благоприятствующего данному событию A.

Каждое событие является или элементарным, или может быть составлено из элементарных событий. Например, событие выпадения четного числа очков при бросании игральной кости, на которой нанесены цифры от 1 до 6, состоит из элементарных событий выпадения цифр 2, 4, 6. Таким образом, рассматриваемому событию благоприятствуют три элементарных события.

При классическом определении за вероятность события A принимается отношение числа элементарных событий, благоприятствующих событию A, к общему числу элементарных событий

,

где P(A) – вероятность события A, m – число элементарных событий, благоприятствующих событию A, n – общее число элементарных событий.

Статистическое определение вероятности связано с понятием относительной частоты события. Относительная частота события вычисляется по формуле:

,

где – число появления события A в серии из опытов.

С увеличением числа опытов относительная частота обычно стабилизируется около некоторой постоянной величины.

При статистическом определении вероятности за вероятностьсобытия A принимают то число, относительно которого стабилизируется относительная частота при увеличении числа опытов.

Из определения вероятности события следует, что .

Теоремы сложения и умножения вероятностей

В задачах, использующих вероятностные количественные характеристики, приходится по вероятностям одних событий оценивать вероятности других событий. Для этого используют различные соотношения, в основе которых лежат теоремы теории вероятностей.

Теорема сложения вероятностей. Вероятность суммы несовместных событий равна сумме вероятностей этих событий:

.

Если в единичном опыте обязательно должно произойти одно из событий , то такая группа событий называется полной группой событий. Сумма вероятностей несовместных событий, образующих полную группу, равна единице: .

Например, при бросании игральной кости, возможно появление одного из чисел: 1, 2, 3, 4, 5, 6. Вероятность каждого появления при единичном бросании . Следовательно,

.

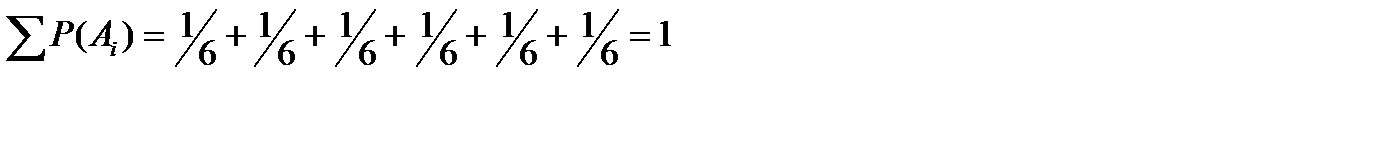В ряде случаев вероятности появления одних событий зависят от того, произошло ли другое событие или нет. Вероятность события A, вычисленная при условии, что имело место другое событие B, называется условной вероятностью события A и обозначается P(A/B) или .

Например, при бросании игральной кости может наступить событие B: «четное число очков» и событие A: «число очков меньше 6». Эти события могут произойти одновременно, т.е. совместны, поэтому можно поставить вопрос о вероятности P(AB) их совместного появления. Эту задачу решает следующая теорема.

Теорема умножения вероятностей. Вероятность произведения двух событий равна произведению вероятности одного из них на условную вероятность другого, вычисленную при условии, что первое событие имело место:

.

Если же появление одного из событий не меняет вероятности появления другого, то события называются независимыми. Вероятность произведения независимых событий равна произведению вероятностей каждого события:

.

Для нашего примера можно определить: , т.к. четных очков – три (2, 4, 6) из шести возможных; , т.к. событию A отвечает только два варианта (2 и 4). Тогда условная вероятность наступления события A при появлении события B:

.

Другой пример. Бросается два кубика отдельно друг от друга. Какова вероятность того, что на первом выпадет четное количество очков (событие A), а на втором число очков будет меньше пяти (событие B)?

В данном случае ясно, что повлиять друг на друга эти события не могут – они независимы. Вероятности: ; , следовательно, вероятность совместного появления обоих событий:

.