Приклади розв’язання задач.

Приклад 1. Побудувати ряд розподілу суми очок на кістці доміно. Знайти моду, математичне сподівання, дисперсію і стандартне відхилення суми очок.

Розв’язання. Як відомо, кістка доміно має два поля, на яких знаходяться числа від 0 до 6. Всього кісток 28, а сума очок на кістці приймає цілі значення від 0 до 12. Усі можливі комбінації чисел на кістці і відповідні суми очок зручно подати за допомогою таблиці, яка наведена нижче.

У першому рядку таблиці розташовані числа очок на одному полі, а у першому стовпчику на другому полі. У полі таблиці знаходяться суми очок на кістці. Половину (нижню) таблиці залишено порожньою внаслідок симетрії суми числа очок.

Ймовірність числа очок і (на основі класичного означення ймовірності визначається за формулою)

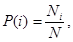
де N_i – число кісток (клітинок у таблиці), що містять суму і (і=1…6), N – загальне число кісток (N=28).

Шляхом підрахунку клітинок визначаємо N_i для і=1…6 і розраховуємо відповідні ймовірності. Ряд розподілу суми очок і подано у наступній таблиці:

і

Ni

P(i)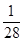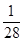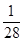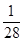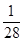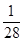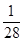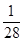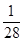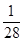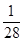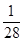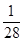

Мода mрозподілу, тобто значення випадкової величини, якому відповідає найбільша ймовірність, дорівнює

m = 6,

а відповідна ймовірність

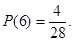
Математичне сподівання Мсуми очок розраховуємо за формулою

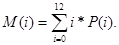
Підставляючи чисельні значення з таблиці, знаходимо:

M(i)=6.

Дисперсія D(i) суми очок розраховується за формулою

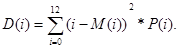
Підставляючи чисельні значення з таблиці, знаходимо:

D(i)=9.

Стандартне σ(i) відхилення суми очок дорівнює

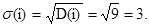
Приклад 2. Дискретна випадкова величина Х задана наступним рядом розподілу:

Xi
P(Xi)	0.1	0.2	0.5	0.2

Записати функцію розподілу випадкової величини, визначити її математичне сподівання та дисперсію. Визначити ймовірність приналежності випадкової величини проміжку [1.5;5.4]

Розв’язання. Функція F(x)розподілу випадкової величини співставляє кожному значенню аргументу (неперервного !) ймовірність того, що випадкова величина буде меншою від аргументу функції. Усі можливі значення даної дискретної випадкової величини наведені у рядку розподілу. Можливі значення випадкової величини Х розбивають область визначення D(F(x))аргументу функції розподілу F(x)на 5 проміжків:

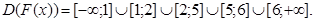
Визначимо функцію розподілу на кожному з цих проміжків. Виходимо з того, що ряд розподілу містить усі можливі значення випадкової величини.

Очевидно, випадкова величина ніяк не може прийняти значення, менше ніж і. Це означає, що подія X<1є неможливою, тобто P(X<1)=0, або

F(x)=0 при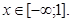

Значень випадкової величини, менших від чисел із проміжку [1;2], існує рівно одне – це Х = 1 , яке має ймовірність 0,1. Отже, подія X<x при 1<x<2 виникає з ймовірністю 0,1, тобто для функції розподілу маємо

F(x)=0.1 при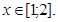

Переходимо до наступного проміжку значень аргументу 1<x<5. Значень випадкової величини, менших ніж, будь-яке число із проміжку [2;5], існує два: це X = 1та Х = 2,які мають ймовірності відповідно 0,1 та 0,2. Отже, подія X<xна проміжку 1<x<5 є об’єднанням подій X = 1або Х = 2, які є несумісними і незалежними. Таким чином, за теоремою додавання ймовірностей маємо на проміжку [1;2]:

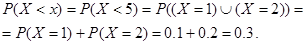
або

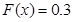при

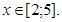
Аналогічним шляхом для значень х із проміжку [5;6] встановлюємо, що є три можливих значення випадкової величини, які задовольняють умові X<x:

X = 1, X = 2 та Х = 5, - так що випадкова подія X<x при 5<x<6 є об’єднанням трьох несумісних подій X = 1, X = 2 та Х = 5 , а її ймовірність визначається за формулою додавання ймовірностей:

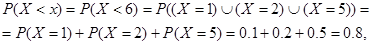
або

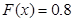при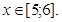

Нарешті, для будь-якого значення х із проміжку 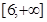подія X<x є достеменною, тобто виконується завжди (немає значень випадкової величини більших за 6). Ймовірність достеменної події дорівнює 1, отже на проміжку x>6 маємо

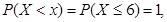
або

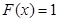при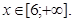

Остаточно записуємо функцію розподілу:

при x<1; при 1<x<2; при 2<x<5; при 5<x<6; при x>6;

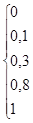
Математичне сподівання Мсуми очок розраховуємо за формулою

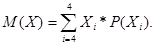
Підставляючи чисельні значення з таблиці, знаходимо:

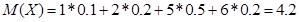
Дисперсія D(i) суми очок розраховується за формулою

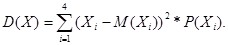
Підставляючи чисельні значення з таблиці, знаходимо:

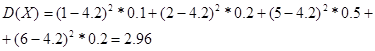
Ймовірність того, що значення випадкової величини Х буде знаходитись у проміжку [x₁;x₂], розраховується за формулою =

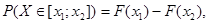
де F(x) – функція розподілу випадкової величини.

За побудованою вище функцією розподілу знаходимо:

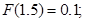
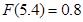
І обчислюємо шукану ймовірність

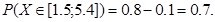
Приклад 3. Час t виготовлення лікарського препарату провізором є рівномірно розподіленою випадковою величиною на інтервалі від 10 до 25 хвилин. Знайти:

а) Вираз функції густини розподілу та вираз функції розподілу часу виготовлення препарату;

б) середній час виготовлення препарату та його дисперсію і стандартне відхилення;

в)ймовірність того, що препарат буде виготовлено за час не більше 15 хвилин.

Розв’язання а) Функцію густини розподілу часу виготовлення препарату f(t) визначаємо, виходячи з означення рівномірного розподілу : за межами проміжку [10 хв; 25 хв.] густина розподілу дорівнює нулю, а в межах цього проміжку вона є оберненою величиною до ширини проміжку, тобто

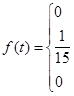
Функція розподілу F(τ) визначається шляхом інтегрування функції густини розподілу f(t) в межах від -∞ до τ

F(τ)=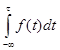

Інтегруючи окремо по інтегралах визначення функції густини розподілу, знаходимо:

F(τ)=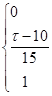

б) Середній час виготовлення препарату T визнаається як його матиматичне сподівання:

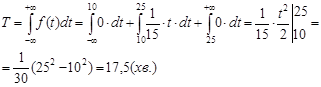
Дисперсія D(t) часу виготовлення дорівнює:

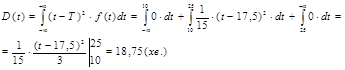
Стандартне відхилення 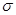₁ часу виготовлення препарату дорівнює:

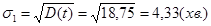
а) Ймовірність того, що час виготовлення препарату буде в межах від t₁ до t₂ може бути визначена за допомогою функції розділу за формулою

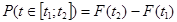
або за допомогою функції густини розподілу за формулою

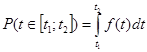
Скористаємось першою формулою. Умова “час виготовлення препарату не більше 15 хв.” Означає, що час виготовлення препарату належить до інтервалу [- ;15]:

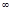t [- ;15]

За знайденою у п.б.) функцією розподілу визначаємо:

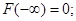
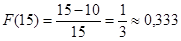
Шукана ймовірність дорівнює:

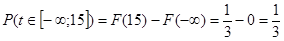
Приклад 6.4. Неперервна випадкова величина X задана функцією густини розподілу ймовірності

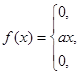
а) Знайти константу а і вираз функції розподілу.

Розв’язання а)Константу а визначаємо за допомогою умови нормування:

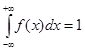
Проінтегруємо функцію густини розподілу:

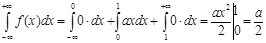
У відповідності з умовою нормування звідси отримуємо рівняння

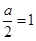
Звідки

а=2.

Отже, функція густини розподілу є

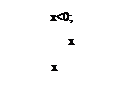
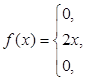
Інтегруючи функцію густини розподілу по трьох інтервалах області визначення, знаходимо функцію розподілу ймовірності величини Х:

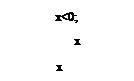
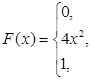
Приклад 6.5. За добу у пологовому будинку народжено 5 немовлят. Ймовірність народження хлопчика дорівнює 0,52. Знайти ймовірність того, серед народжених

а) рівно троє хлопчиків;

б) не менше трьох дівчаток.

а) Знайти константу а і вираз функції розподілу

Розв’язання. Оскільки окремі народження є незалежними подіями і ймовірності народження хлопчика у кожному народженні є однаковими, то задача відповідає умовам випробувань Бернуллі (послідовні незалежні випробування).

Введемо позначення випадкових подій: А – народження хлопчика, А₃ – народження трьох хлопчиків з п’яти дітей, В – народження дівчинки, В_і – народження і дівчаток з п’яти дітей, С – народження не менше трьох дівчаток з п’яти дітей.

За умовою маємо

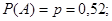
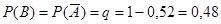
а) Ймовірність того, що серед народжених віно троє хлопчиків визначаємо за формулою Бернуллі:

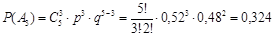
б) Подія С полягає у народженні або 3, або 4, або 5 дівчаток, які являють собою несумісні події, так що подія С є їх об’єднанням. Отже, у відповідності теоремою додавання ймовірностей і формулою Бернуллі, для ймовірності народження не менше трьох дівчаток маємо:

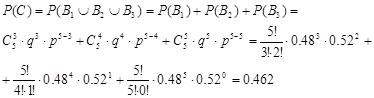
Приклад 6.6. В результаті вакцинації імунітет від захворювання формується ймовірність 0.999. Вакцинацію пройшли 4000 дітей. Яка ймовірність того імунітету не набуло двоє дітей?

Розв’язання. Ймовірність події “не набуття імунітету”, яку позначимо N, як події протилежної до події “набуття імунітету”, яку позначимо I,становить

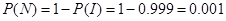
Оскільки число випробувань велике (4000) і ймовірність події “ненабуття імунітету” постійна і достатньо мала (0.001), то можна вважати, що число дітей, що це набули імунітету, описується розподілом Пуассона (закон рідкісних подій).

Ймовірність m-разового здійснення у серії n випробувань випадкової події, яка має розподіл Пуассона, визначається за формулою Пуассона:

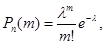
де 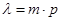- параметр розподілу,

n-число випробувань,

p-ймовірність здійснення події.

У нас n=4000, m=2, p=0.001, 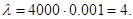Підставляючи чисельні значення до формули Пуассона, знаходимо

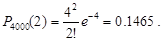
Приклад 6.7. Зріст жінок (см) має нормальний розподіл з математичним сподіванням 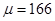см і стандартним відхиленням 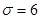см. Яка частина жінок має зріст

а) менше 180 см;

б) в межах [160;175] см?

Розв’язання. Задана випадкова величина має нормальний розподіл N(166;6). Ймовірність приналежності випадкової величини Х, що має нормальний розподіл 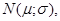до проміжку [x₁;x₂] дорівнює

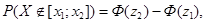
де 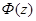- функція розподілу ймовірності стандартного нормального розподілу N(0;1) (інтеграл ймовірності);

z – нормалізована змінна

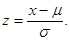
а) Умова “зріст менше 180 см” означає приналежність зросту до інтервалу [- ;180]. Переходимо до нормалізованої змінної z, для чого обчислюємо її значення на межах інтервалу

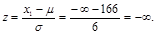
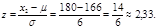
Знаходимо за таблицями значень функції Ф(z)

Ф(2,33)=0,99; Ф(- )=0.

Шукана ймовірність дорівнює

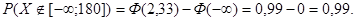
б) Переходимо до нормалізованої змінної:

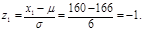
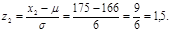
Знаходимо за таблицями значень функції Ф(z)

Ф(-1)=1-Ф(1)=1-0,841=0,159; Ф(1,5)=0,933

І розраховуємо шукану ймовірність

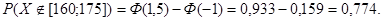
Тема 3. Елементи математичної статистики.