Пример решения смешанной игры

Найти решение игры с матрицей, заданной табл. 10.

Таблица 10 Таблица 11

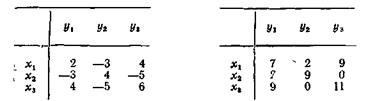
Прежде всего убеждаемся, что в игре отсутствует седловая точка и ни одна из стратегий не доминирует над другими. Для того чтобы не иметь дела с отрицательными элементами матрицы игры, добавляем к каждому элементу матрицы число 5. Матрица игры принимает вид табл. 11.

Уравнения запишутся в виде

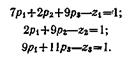
Решение этих уравнений должно удовлетворять условию мини­мума линейной формы

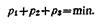
Решая полученную задачу линейного программирования, на­ходим:

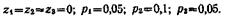
Из выражения (4) находим:

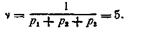
При этом

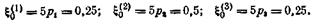
Для нахождения оптимальной смешанной стратегии второго игрока составляем одно уравнение вида

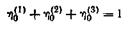
и двауравнения вида

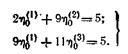
Решая совместно триполученных уравнения, находим:

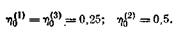
Вспоминая, что ко всем элементам матрицы игры было прибав­лено число 5, находим цену игры v—5=0.

Кооперативные игры

В конфликтных ситуациях участники могут объединяться в коалиции и выступать группами друг против друга. Такие игры называются кооперативными и в них помимо ранее изложенных проблем (поиск оптимальных стратегий) встает необходимость правильного дележа выигрыша между участниками коалиции (оценки целесообразности вступления в коалицию).

В дальнейшем рассмотрим игры, в которых определяется наиболее выгодная структура коалиций, с помощью которой каждый из участников определяет для себя целесообразность вступления в ту или иную коалицию. Целесообразность определяется величиной выигрыша участника в результате проведенной игры.

Допустим, в игре участвует множество {N} участников. Из этого множества могут быть сформированы коалиции (группы) числом участников 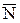. Число возможных коалиций определяется по формуле .

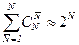При правильно выбранной стратегии 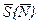коалиция сможет получить максимальный выигрыш 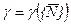, который называется характеристической функцией.

Считается, что если имеются рациональные коалиции , то сумма выигрыша всех коалиций должна быть меньше или равна выигрышу коалиции объемом N (когда все участники в одной группе), т.е.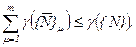

Считается, что в результате деления выигрыша каждому участнику коалиции достанется выигрыш 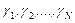. Игра и коалиции составлены правильно, если выигрыш участника коалиции 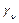окажется больше или равен выигрышу участника, выступающего самостоятельно:

.

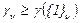Распределение выигрыша или оценка участия в той или иной коалиции между участниками математически задается в виде вектора дележа

.

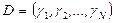При составлении вектора дележа учитываются два выше рассмотренных условия:

Основной целью кооперативной игры является поиск оптимального вектора дележа. Поиск осуществляется методом сравнения векторов дележа. Вектор дележа называется доминирующим (лучшим), если для каждого его участника 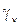больше, чем 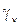другого вектора.

Пусть имеем два вектора дележа:

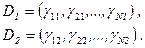
Считается, что если 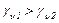, то вектор 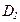доминирует над вектором .

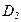Оптимальный вектор называется ядром игры 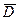. Дележ с помощью ядра игры называется равноценным делением (оптимальный дележ), в котором 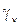максимальный.