Определение параметров неполиномиальных зависимостей с помощью МНК

В результате метрологических исследований нередко приходится сталкиваться со случаем, когда при определении нелинейной зависимости повышение степени полинома в разумных пределах не приводит к существенному уменьшению погрешности аппроксимации. В этом случае применяют следующие приемы.

1. Разбиение области определения функции на несколько участков с последующей аппроксимацией ее на каждом из участков.

2. Преобразование функции 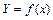в линейную зависимость 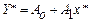путем замены переменных .
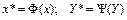Этот прием хорошо реализуется для функций следующего вида:

а) показательная 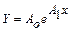, для которой в результате замены переменной 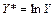, получаем 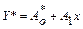, где ;

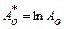б) степенная 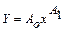, для которой в результате замены переменных 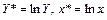, получаем 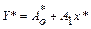, где ;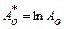

в) логарифмическая 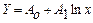, для которой в результате замены переменной 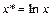получаем ;

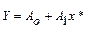г) гиперболическая , для которой в результате замены переменной 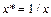получаем ;

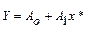д) дробно-линейная функция первого вида 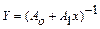, для которой в результате замены переменной 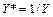получаем ;

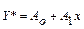е) дробно-линейная функция второго вида 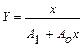, для которой в результате замены переменных 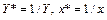, получаем .

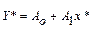Графики перечисленных функций приведены на рис. 3.8.

	Рисунок 3.8 - Графики аппроксимирующих функций

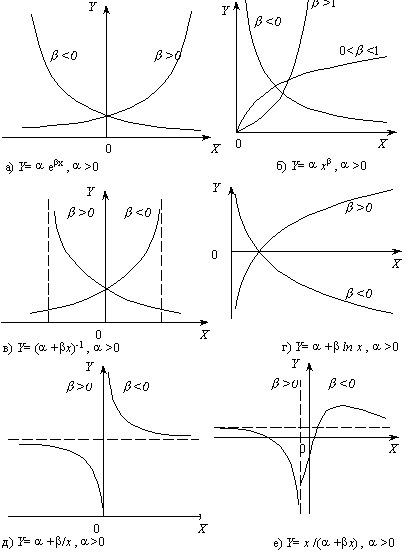При определении погрешности нахождения оценок 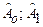, необходимо помнить, что в случаях показательной и степенной функции параметр 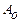связан с параметром 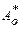выражением .

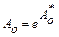Поэтому погрешност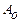и и 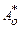будут связаны соотношением .

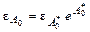3. Линеаризация нелинейных уравнений методом последовательных приближений

Общий метод решения этой задачи основан на допущении, что несовместность условных уравнений невелика, т.е. их невязки малы. Тогда, взяв из условной системы столько уравнений, сколько в ней неизвестных,

их решением находим начальные оценки неизвестных . Полагая далее, что 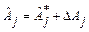и подставляя эти выражения в условные уравнения, раскладываем условные уравнения в ряды. Сохраняя лишь члены с первыми степенями поправок 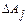, получим

.

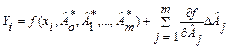Переписав полученное выражение в виде

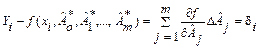, (3.52)

можно видеть, что мы получили условную систему линейных уравнений относительно поправок 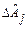. Решение этой системы с помощью МНК дает нам их оценки и СКО. Тогда 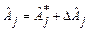. Поскольку 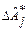- неслучайные величины, то 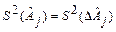. Получив оценки 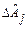, можно сделать второе приближение и т.д.