Плоские электромагнитные волны в однородной изотропной среде с проводимостью, отличной от нуля.

При распространении в реальных средах электромагнитные волны испытывают затухание, происходит потеря энергии, переносимой этими волнами. Основные потери в среде связаны с проводимостью, отличной от нуля. Электромагнитная волна вызывает в такой среде токи проводимости с плотностью 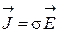, на поддержание которых расходуется часть энергии волны, в результате чего выделяется тепло (джоулевы потери). Тепловые потери в среде могут быть также обусловлены инерционностью процессов поляризованности и намагниченности сред. Но в большинстве практических случаев при рассмотрении электромагнитных волн радиодиапазона среды безинерционны и эти потери не приходится учитывать.

Рассмотрим однородную изотропную среду с параметрами 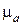и комплексной диэлектрической проницаемостью

. (7.1).

В однородной изотропной среде при наличии потерь поле плоской волны так же описывается формулами (6.34), (6.35), если в них учесть, что волновое число становится комплексной величиной

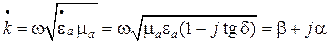. (7.2).

В выражении (7.2) за β обозначена реальная часть комплексного волнового числа, за α – мнимая часть. Для дальнейшего анализа необходимо определить β и α и обосновать знак перед мнимой частью. Возведя в квадрат обе части равенства (7.2), разделяя вещественную и мнимую части, получаем систему двух алгебраических уравнений относительно β и α

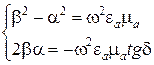. (7.3).

Из (7.3) следует, что

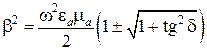. (7.4).

Так как реальная часть комплексного волнового числа не может быть отрицательной величиной, то в формуле (7.4) нужно выбрать знак «+». Для коэффициента фазы β, характеризующего изменение фазы бегущей волны, получаем расчетную формулу

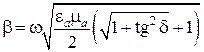. (7.5).

Отметим, что коэффициент фазы β в среде с 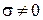больше коэффициента фазы 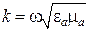в среде без потерь ( 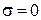) с теми же значениями 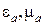. Из системы (7.3) получаем выражение для коэффициента затухания α, характеризующего уменьшение амплитуды бегущей волны

. (7.6)

Далее, нужно учесть, что из второго уравнения системы (7.3) следует, что β и α имеют разные знаки, т. е. возможны равенства

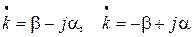. (7.7).

Рассмотрим волновой множитель (оператор бегущей волны) е^-jkz в выражениях (6.34), (6.35). В среде с потерями, учитывая (7.7), функция 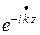может быть записана одним из двух способов

. (7.8)

По предположению (лекция 6) источник находится со стороны отрицательных значений координаты z и волна распространяется вдоль оси z. Этому условию соответствует первое выражение (7.8), в котором множитель 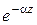учитывает экспоненциальное уменьшение амплитуды из-за потерь на нагревание среды при 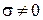. В соответствии с этим выбором комплексное волновое число записывается

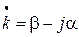. (7.9).

В выражении (7.9) коэффициент фазы β вычисляется по формуле (7.5), коэффициент затухания α по (7.6), обе формулы справедливы при любой проводимости среды.

Комплексная диэлектрическая проницаемость (7.1) входит в характеристическое сопротивление среды, которое становится также комплексной величиной. В рассматриваемом случае

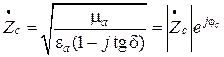, (7.10)

где .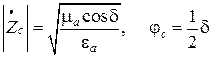

Подставляя выражения (7.9), (7.10) в формулы (6.34), (6.35), получаем поле плоской однородной волны, распространяющейся вдоль оси z в среде с проводимостью, отличной от нуля

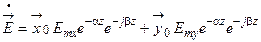; (7.11)

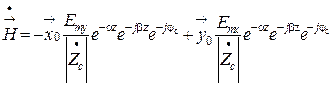. (7.12)

При изменении удельной проводимости σ от нуля до бесконечности фаза φ_с увеличивается от нуля до 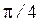, а модуль 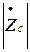убывает от 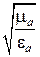до нуля. Наличие потерь приводит к уменьшению абсолютной величины характеристического сопротивления, то есть к увеличению 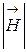при заданном значении 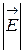. Это обусловлено тем, что величина 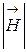определяется как током проводимости, так и током смещения. В среде с σ = 0 существуют только токи смещения, которые при одинаковых значениях 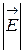и 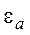остаются прежними и в среде с потерями (σ ≠ 0), а возникшие токи проводимости увеличивают лишь магнитное поле.

Для дальнейшего анализа плоской волны в среде с потерями рассмотрим случай, когда вектор 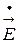(7.11) имеет одну составляющую, например, 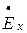, а вектор 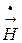(7.12) имеет соответственно 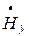. Перейдем к мгновенным значениям этих составляющих

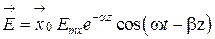, (7.13)

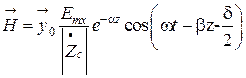. (7.14)

Амплитуды векторов 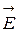и 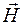экспоненциально убывают вдоль оси z, вектор 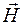опаздывает по фазе относительно вектора 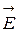на величину 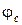, равную половине угла потерь ( 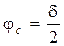). На рис. 7.1 приведена зависимость мгновенных значений векторов 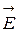и 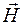от времени t в некоторой фиксированной точке пространства z = z₀, а на рис. 7.2 – зависимость мгновенных значений векторов 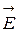и 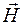от координаты z в некоторый момент времени t = t₀.

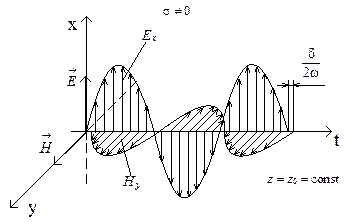
Рис. 7.1. Изменение поля плоской волны во времени

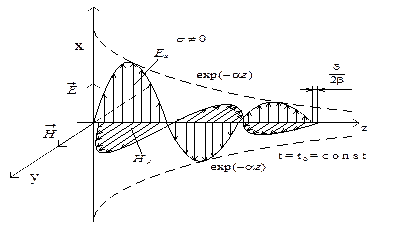
Рис. 7.2. Изменение поля плоской волны в пространстве

Фазовая скорость плоской волны определяется по общей формуле, как отношение частоты к коэффициенту фазы

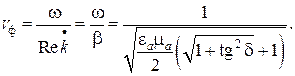(7.15)

Фазовая скорость плоской волны в среде с потерями меньше чем фазовая скорость плоской волны в среде без потерь ( 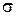= 0) с теми же параметрам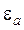и и 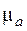. Как видно из (7.15) фазовая скорость зависит от частоты 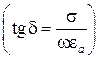, с увеличением частоты она возрастает и стремится к фазовой скорости в среде без потерь . Кроме того, величина V_ф зависит от проводимости среды: при одинаковой частоте она будет меньше в среде с большей проводимостью.

Длина волны в среде с потерями

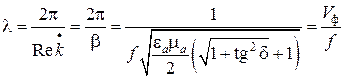(7.16)

Длина волны при фиксированной частоте убывает с увеличением проводимости .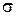

Коэффициент затухания α (7.6) это действительная величина, которая, подобно коэффициенту фазы, имеет размерность 1/м. Экспонента 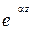показывает во сколько раз уменьшаются амплитуды векторов 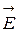и 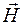по прохождению расстояния в z (м). Поскольку величина затухания может меняться в больших пределах в разных средах, то удобно ввести логарифмический масштаб представления коэффициента затухания. Для этого используется отношение амплитуд напряженности электрического поля по прохождению расстояния в один метр

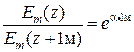. (7.17).

Натуральный логарифм (7.17) определяет коэффициент затухания в неперах на метр (Нп/м)

.

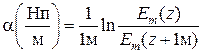В технических расчетах часто используют другую логарифмическую единицу – децибелы на метр (дБ/м), которую определяют как двадцать десятичных логарифмов того же отношения амплитуд (7.17)

.

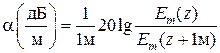Поскольку ln 10=2,303, а lg e=0,4343, то 1Нп = 8,686 дБ и 1 дБ=0,1151 Нп. В названии коэффициента затухания использованы имена известных ученых – Непера и Белла (д – децимальная приставка). Если плоская волна распространяется в однородной среде и проходит расстояние l (м), то общее затухание (потери) на трассе рассчитываются в логарифмических единицах следующим образом:

.

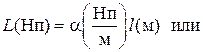
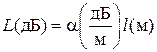Расстояние, по прохождению которого электромагнитная волна ослабевает в е = 2,718 раз, называется глубиной проникновения волны в среду и определяется как Δ = (Δ – заглавная буква дельта греческого алфавита).

Распространение волны сопровождается переносом энергии. В среде с 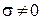комплексный вектор Пойнтинга в общем случае, когда векторы 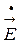и 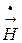имеют по две составляющие (7.11), (7.12) рассчитывается следующим образом:

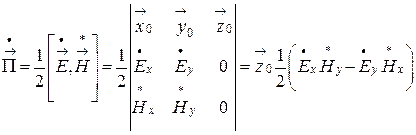.(7.18)

В рассматриваемом случае, когда вектор 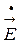имеет одну составляющую, а вектор 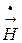– одну 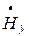, комплексный вектор Пойнтинга равен

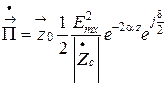(7.19)

и содержит как действительную, так и мнимую части. Это означает, что имеется как активный, так и реактивный поток мощности. Средняя за период плотность потока мощности экспоненциально убывает вдоль оси z

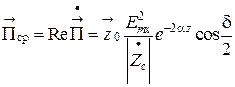. (7.20)

Возникновение плотности потока реактивной энергии в среде с 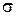≠ 0 может быть объяснено следующим образом. При распространении электромагнитной волны в среде возникают электрические токи с плотностью 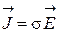, на поддержание которых расходуется часть энергии волны. В свою очередь, возникшие в среде электрические токи излучают электромагнитное поле, создают вторичную электромагнитную волну, которая складывается с первичной и происходит непрерывный обмен энергией между волной и средой, что и приводит к возникновению потока реактивной мощности.

Скорость распространения энергии вычисляется по формуле (4.65)

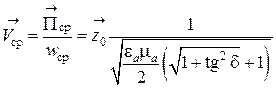. (7.21)

Как видно из (7.21) скорость распространения энергии зависит от частоты. Основное отличие параметров плоской волны, распространяющейся в среде с конечной проводимостью и в среде с 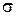= 0 состоит в том, что в среде без потерь параметры волны ( 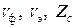и др.) одинаковы при любых частотах, а в среде с проводимостью они зависят от частоты. Зависимость фазовой скорости волны от частоты называется дисперсией. Следует отметить, что если есть необходимость учесть другие потери, например, магнитные, то следует воспользоваться изложенным способом определения коэффициента фазы, коэффициента затухания и характеристического сопротивления среды и всеми последующими преобразованиями.

Рассмотрим два частных случая реальных сред: диэлектрики с малыми потерями и хорошо проводящие среды (проводники).