Применение вычетов к вычислению интегралов. (Основная теорема теории вычетов)

Из определения предыдущего параграфа непосредственно следует, что интеграл от аналитической функции по замкнутому контуру, содержащему внутри себя единственную особую точку выражается через вычет в этой точке: 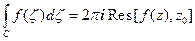. Эта формула легко обобщается следующей теоремой.

Теорема(Основная теорема теории вычетов). Пусть функция f(z) является аналитической всюду в ограниченной замкнутой области G с границей Г за исключением конечного числа изолированных особых точек z_k (k = 1,2,…,n), лежащих внутри области. Тогда

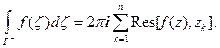
Доказательство. Выделим каждую особую точку z_k замкнутым контуром γ_k , лежащим в области G и содержащим внутри себя эту точку (рис.4).

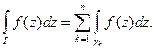Функция f(z) является аналитической в области, ограниченной контурами Г и γ₁,…, γ_n. По следствию теорем п. 2.2 верна формула Отсюда и из предыдущего параграфа следует утверждение теоремы.

Данная формула часто используется для вычисления интегралов от комплексных функций.

Пример. Вычислить интеграл 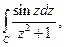где С − окружность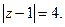

Решение.Функция имеет два полюса первого порядка, лежащие внутри окружности С. Оба вычета легко определяются (п.2.10). Итак: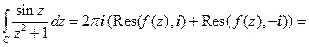

.

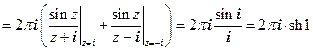2.11 Вычет функции в бесконечно удаленной особой точке.

Определение.Вычетом аналитической функции f(z) в точке z = ∞ называется значение интеграла 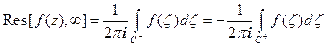, где С – произвольный замкнутый контур, вне которого f(z) – аналитическая и не имеет особых точек, отличных от ∞. Фактически, контур С ⁻ является границей окрестности бесконечно удаленной точки, при обходе которой область остается слева. В силу определения коэффициентов ряда Лорана

получаем: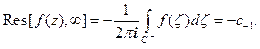

Пример.Вычислить Res .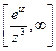

Решение. .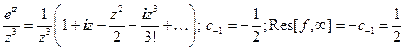

Из полученных формул следует утверждение:

Теорема.Пусть функция f(z) регулярна на расширенной комплексной плоскости, за исключением конечного числа изолированных особых точек z₁,…,z_n−1, z_n = ∞. Тогда

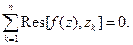
Доказательство.Пусть контур С содержит внутри себя все конечные особые точки. В силу

теоремы из п.2.11 и последней полученной формулы имеем: 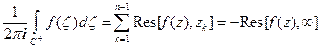. Из второй части равенства следует утверждение теоремы.

Пример. Рассмотрим последний пример: Res[f,0] = 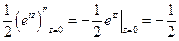= − Res[f,∞],

т.е. сумма всех вычетов расширенной комплексной плоскости равна нулю.

Выведенная формула может быть записана следующим образом:

.

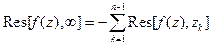В такой форме она применяется как при вычислении вычета в бесконечно удаленной точке,

так и справа налево при вычислении интегралов в том случае, когда внутри контура С находится несколько полюсов высокого порядка, а вычет в бесконечно удаленной точке может быть найден достаточно просто непосредственно.

Замечание. Из последней формулы следует, что вычет функции, имеющей в бесконечно удаленной точке устранимую особенность, может быть отличным от нуля.

Вопросы для самопроверки.

1. При каком условии 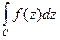не зависит от пути интегрирования?

2. Применима ли формула Коши для вычисления интеграла .

3. Какова связь между нулями и полюсами функции?

4. Чему равна сумма вычетов функции во всех конечных особых точках?

3.Операционное исчисление.

В этом разделе рассматривается одно из основных приложений ТФКП - решение дифференциальных уравнений (как обыкновенных, так и с частными производными).

3.1. Интеграл Фурье

Напомним основные результаты разложения функций в тригонометрические ряды Фурье.

Пусть в промежутке 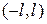функция 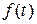удовлетворяет условиям Дирихле, а именно:

а) ограничена на этом отрезке;

б) кусочно-непрерывна на нем (имеет конечное число точек разрыва первого рода);

в) кусочно-монотонная (в частности, имеет лишь конечное число экстремумов).

Из теории тригонометрических рядов следует, что ряд

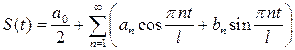(3.1)

представляет собой периодическую функцию с периодом 2l и сходится к функции f(t) на интервале 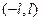. По теореме Дирихле:

1) в точках непрерывности сумма ряда равна значению функции: ;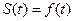

2) в точках разрыва t₁ сумма ряда 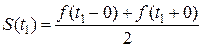(включая концы интервала, если ).

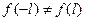Коэффициенты ряда (1.1) определяются по формулам Эйлера-Фурье:

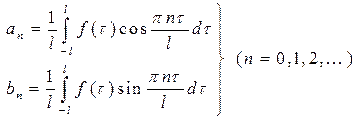(3.2)

Мы будем рассматривать полученный ряд Фурье только на интервале 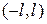. В этом случае формулу (3.1) можно написать в виде: 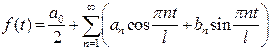(3,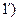

Легко видеть, что коэффициенты 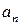и 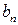удовлетворяют условиям: , 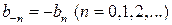. Поэтому формула (3, 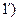может быть записана в виде 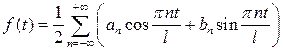или, с учетом формул (3.2),

,

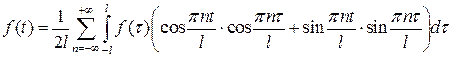откуда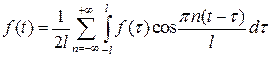

Если ввести обозначения:

,

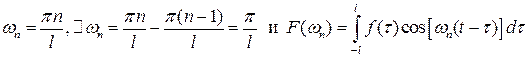то последняя формула будет иметь вид: 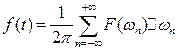. (3.3)

Пусть функция 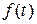абсолютно интегрируема на промежутке 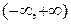, т.е.

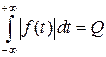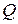( − конечное число),

Можно доказать, что при 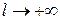равенство (3.3) перейдёт в равенство:

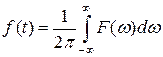, или 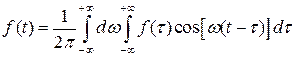. (3.4)

Интеграл, стоящий в правой части равенства (3.4), называется интегралом Фурье.

Замечая, далее, что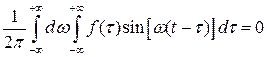

Пользуясь нечетностью функции 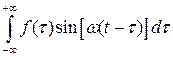по аргументу 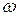, преобразуем формулу (3.4): 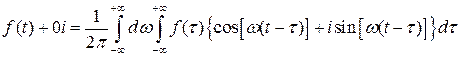, откуда

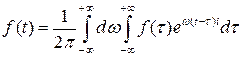. (3.5)

Последний интеграл называется интегралом Фурье в комплексной форме.