Автокорреляция в остатках. Критерий Дарбина-Уотсона

Автокорреляция остатков - наличие корреляции между остатками текущих и предыдущих (последующих) наблюдений. Коэффициент корреляции между e_i и e_j , где e_i — остатки текущих наблюдений, e_j — остатки предыдущих наблю­дений, может быть определен по обычной формуле линейного коэффициента корреляции . Если этот коэффициент окажется существенно отличным от ну­ля, то остатки автокоррелированы и функция плотности вероят­ности F(e) зависит j-й точки наблюдения и от распределения значений остатков в других точках наблюдения. Для регрессионных моделей по статической информации ав­токорреляция остатков может быть подсчитана, если наблюдения упорядочены по фактору х. Отсутствие автокорреляции остаточных величин обеспечива­ет состоятельность и эффективность оценок коэффициентов ре­грессии. Особенно актуально соблюдение данной предпосылки МНК при построении регрессионных моделей по рядам динами­ки, где ввиду наличия тенденции последующие уровни динами­ческого ряда, как правило, зависят от своих предыдущих уров­ней.

Два метода опреде­ления автокорреляции остатков: Первый метод — это построение графика зависимости остатков от времени и визуальное определение наличия или отсутствия автокорреляции. Второй метод — использо­вание критерия Дарбина — Уотсона и расчет величины

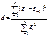(1)Таким образом, d есть отношение суммы квадратов разностей последовательных значений остатков к остаточной сумме квадра­тов по модели регрессии. Можно предположить _у2,что: 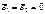, предположим также 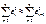Коэффициент автокорреляции остатков оп­ределяется как

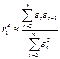С учетом (3) имеем: 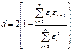Таким образом, если в остатках существует полная положи­тельная автокорреляция и 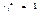, то d= 0. Если в остатках полная отрицательная автокорреляция, то 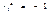и, следовательно, d= 4.Если автокорреляция остатков отсутствует, то 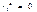и d = 2. Следовательно, 0≤d≤4

19. Ошибки спецификации уравнения регрессии. Спецификация регрессии – отбор факторных переменных, включаемых в регрессионную модель и определение формы модели.

Гипотеза о статистической значимости оценок может быть правильной и неправильной, поэтому возникает необходимость ее проверки. В результате статистической проверки гипотезы в двух случаях может быть принято неправильное решение, т.е. могут быть допущены ошибки двух типов.

Ошибка первого рода состоит в том, что будет опровергнута правильная гипотеза. Обычно ее называют уровнем значимости α – т.е. вероятность совершить ошибку первого рода. Обычно уровень значимости α принимают равным 0,05 или 0,01 (например если α=0,05 то в 5 случаях из 100 имеется риск допустить ошибку первого рода).

Ошибка второго рода состоит в том что будет принята неправильная гипотеза. Число степеней свободы ν=n-k-1, где n-число наблюдений (объем выборки), k-число параметров при факторных переменных в уравнении регрессии (для однофакторной регрессии k=1 и ν=n-2). 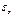— случайная величина, характеризующая отклонения реального значения результативного признака от теоретического.

Случайная величина ε называется также возмущением. Она включает влияние не учтенных в модели факторов, случайных ошибок и особенностей измерения.

От правильно выбранной спецификации модели за­висит величина случайных ошибок: они тем меньше, чем в боль­шей мере теоретические значения результативного признака 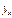подходят к фактическим данным у.

К ошибкам спецификации относятся непра­вильный выбор той или иной математической функции для 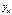, и недоучет в уравнении регрессии какого-либо существенного фактора, т. е. использование парной регрессии вместо множест­венной.

16. Парная и частная корреляция в модели множественной регрессии. Множественный коэффициент корреляции, множественный коэффициент детерминации.

Если имеется одна независимая и одна зависимая переменная, то мерой тесноты их связи служит парный коэффициент корреляции. Если имеется несколько независимых переменных, то необходимо рассчитывать частные коэффициенты корреляции.

Парный и частный коэффициенты корреляции ( 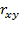) характеризуют тесноту линейной зависимости между двумя переменными соответственно на фоне действия и при исключении влияния всех остальных показателей, входящих в модель.

Они изменяются в пределах от -1 до +1, причем чем ближе коэффициент корреляции к 1, тем сильнее зависимость между переменными. Если коэффициент корреляции больше нуля, то связь положительная, а если меньше нуля — отрицательная.

Множественный коэффициент корреляции (R) характеризует тесноту, линейной связи между одной переменной (результативной) и остальными, входящими в модель; он изменяется в пределах от 0 до 1.

Квадрат множественного коэффициента корреляции называется множественным коэффициентом детерминации (R2). Он характеризует долю дисперсии одной переменной (результативной), обусловленной влиянием всех остальных переменных, входящих в модель.

Коэф. корреляции:

где 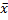и 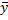– средние значения переменных x и y:

Множественный коэф. корреляции:

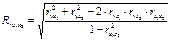
Множественный коэф. детерминации: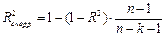

17. Оценка множественной регрессии. Критерий Фишера и Стьюдента.

В общем виде качество эконометрической модели оценивается адекватностью (ее соотношение моделируемому объекту относительно существенных для исследования свойств объекта) и точностью (отклонение теоретического значения от его фактического).

Оценка статистической значимости модели множественной регрессии состоит в сравнение факторной и остаточной дисперсии с использованием F-критерия Фишера. Если фактическое значение этого критерия больше теоретического при заданном уровне значимости α и степени свободы v1=n-1 и v2=n-k-1, то модель признается значимой.

При проверке качества надо также оценить значимость коэффициентов с использованием t-статистики Стьюдента. Если расчетное значение критерия превышает критическое, то коэффициент регрессии считается значимым.

Обобщенный МНК

При нарушении гомоскедастичности (Наличие одинаковой дисперсии. Данные являются гомо-ми, если их вариации соответствуют случайным отклонениям по тому же мн-ву. Это отличается от гетероскедастичности (heteroscedasticity), т. е. наличия различной дисперсии.) и наличии автокорреля­ции ошибок рекомендуется традиционный МНК заменять обобщенным методом. ОМНК применяется к преобразованным данным и позволяет получать оценки, которые обладают не только свойством несмещенности, но и имеют меньшие выборочные дисперсии. Суть ОМНК – минимиз-я обобщенной суммы квадратов отклонений( учет ненулевых ковариаций случ-ой ош-ки для разных наблюденийи непостоянной дисперсии ош-ки)

В общем виде для уравнения yi=a+bxi+ei при где Ki – коэф-т пропор-ти. Модель примет вид: yi=+xi+ei . В ней остаточные величины гетероскедастичны. Предполагая в них отсутствие автокорреляции, можно перейти к уравнению с гомоскедастичными остатками, поделив все переменные, зафик­сированные в ходе i-го наблюдения на . Тогда дисперсия остатков будет величиной постоянной. От регрессии у по х мы перейдем к регрессии на новых переменных: y/ и х/. Уравнение регрессии примет вид: . По отношению к обычной регрессии уравнение с новыми, преобразованными переменными представляет собой взвешен­ную регрессию,в которой переменные у и х взяты с весами . Коэф-т регрессии b можно определить как

Как видим, при использовании обобщенного МНК с целью корректировки гетероскедастичности коэффициент регрессии b представляет собой взвешенную величину по отношению к обычному МНК с весами 1/К.Аналогичный подход возможен не только для уравнения парной, но и для множественной регрессии. Применение в этом случае обобщенного МНК приводит к то­му, что наблюдения с меньшими значениями преобразованных переменных х/К имеют при определении параметров регрессии относительно больший вес, чем с первоначальными переменны­ми