Электрическая емкость уединенного проводника

Рассмотрим уединенный проводник, т. е. проводник, который удален от других проводников, тел и зарядов.

Для уединенного проводника можно записать

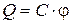
Величину

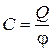(10.1)

называют электроёмкостью (или просто ёмкостью) уединённого проводника.

Ёмкость уединенного проводника определяется зарядом, сообщение которого проводнику изменяет его потенциал на единицу.

Единица электроемкости –фарад(Ф): 1 Ф – ёмкость такого уединенного проводника, потенциал которого изменяется на 1В при сообщении ему заряда в 1 Кл.

Потенциал уединенного шара радиуса R, находящегося в однородной среде с диэлектрической проницаемостью e, равен

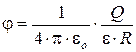
Используя формулу (10.1), получим, что ёмкость шара

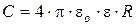(10.2)

Отсюда следует, что ёмкостью в 1 Ф обладал бы уединенный шар, находящийся в вакууме и имеющий радиус

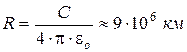
что в 1400 раз больше радиуса Земли (электроёмкость Земли C»0,7 мФ).

Следовательно, фарад – очень маленькая величина, поэтому на практике используются дольные единицы – миллифарад (мФ), микрофарад (мкФ), нанофарад (нФ), пикофарад (пФ).

Конденсаторы

Конденсатор – прибор способный накапливать значительные по величине электрические заряды, иными словами, обладать большой ёмкостью.

Конденсатор состоит из двух проводников (обкладок), разделенных диэлектриком.

Конденсаторам придают такую форму, чтобы поле, создаваемое накапливаемыми зарядами, было сосредоточено в узком зазоре между обкладками конденсатора. Этому условию удовлетворяют:

1) две плоские пластины;

2) два коаксиальных цилиндра;

3) две концентрические сферы.

В зависимости от формы обкладок конденсаторы делятся на плоские, цилиндрические и сферические.

Под ёмкостью конденсатора понимается физическая величина, равная отношению заряда Q, накопленного в конденсаторе, к разности потенциалов (j₁ – j₂) между его обкладками:

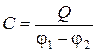. (11.1)

При наличии диэлектрика между обкладками разность потенциалов между ними

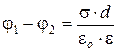
где e – диэлектрическая проницаемость.

Тогда из формулы получим ёмкости плоского конденсатора

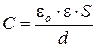(11.2)

Ёмкость цилиндрического конденсатора

Разность потенциалов между обкладками с учётом наличия диэлектрика между обкладками:

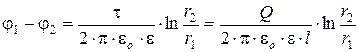
Ёмкость цилиндрического конденсатора:

.

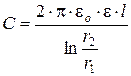Ёмкость сферического конденсатора

Разность потенциалов между двумя точками, лежащими на расстояниях r₁и r₂ (r₂>r₁) от центра заряженной сферической поверхности. С учетом наличия диэлектрика между обкладками

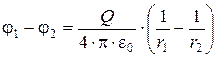
Ёмкость сферического кон­денсатора

.

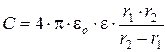Конденсаторы характеризуются пробивным напряжением – разностью потенциалов между обкладками конденсатора, при которой происходит пробой – электрический разряд через слой диэлектрика в конденсаторе. Пробивное напряжение зависит от формы обкладок, свойств диэлектрика и его толщины.

Для увеличения ёмкости и варьирова­ния её возможных значений конденсаторы соединяют в батареи, при этом использу­ется их параллельное и последовательное соединение.

1. Параллельное соединение конденсаторов(рис. 11.1).

У параллельно соединенных конденсаторов разность потенциалов на обкладках конденсаторов одинакова и равна j_А –j_В.

Если ёмкости отдельных конденсаторов С₁, С₂, … С_n,то их заряды равны:

………………..

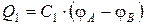
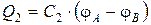
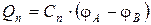
а заряд батареи конденсаторов

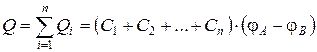
Полная ёмкость батареи

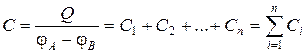
т.е. при параллельном соединении кон­денсаторов она равна сумме ёмкостей отдельных конденсаторов.

2. Последовательное соединение конденсаторов (рис. 11.2).

У последовательно соединенных конденсаторов заряды всех обкладок равны по модулю, а разность потенциалов на зажимах батареи

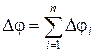
где для любого из рассматриваемых конденсаторов

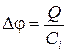
С другой стороны,

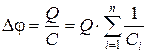
откуда

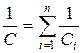
т.е. при последовательном соединении конденсаторов суммируются величины, обратные ёмкостям. Таким образом, при последовательном соединении конденсаторов результирующая емкость C всегда меньше наименьшей ёмкости, используемой в батарее.