Определение точечных оценок числовых характеристик эмпирических законов распределения случайной погрешности

В отличие от самих числовых характеристик их оценки являются случайными величинами, причем их значения и рассеянность зависят от числа экспериментальных данных.

Точечные оценки числовых характеристик должны удовлетворять 3-м требованиям: они должны быть состоятельными, несмещенными и эффективными.

Состоятельной называется оценка, которая с увеличением выборки приближается к истинному значению характеристики

.

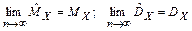По определению математического ожидания

.

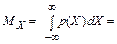
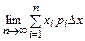Так как каждое значение х_і появляется один раз при общем объеме выборки n, то 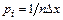, откуда

.

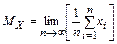При конечном n оценкой М_Х является среднее арифметическое

.

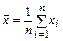Поскольку 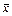появилось из М_Х при ограничении объема выборки, то 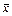является состоятельной оценкой математического ожидания.

По определению дисперсии

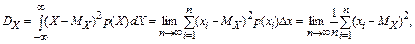
то есть состоятельной оценкой 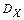является так называемая выборочная дисперсия

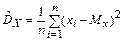. (2.30)

На практике 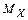неизвестно, поэтому при расчете 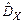математическое ожидание 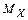заменяют оценкой :

.

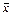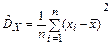Это не влияет на состоятельность , поскольку .

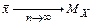Несмещенной называется оценка, математическое ожидание которой равно самой характеристике.

.

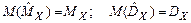Проверим несмещенность среднего арифметического

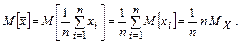
Таким образом, среднее арифметическое является несмещенной оценкой математического ожидания результатов многократных наблюдений при любом законе распределения.

Проверим несмещенность оценки дисперсии (2.30)

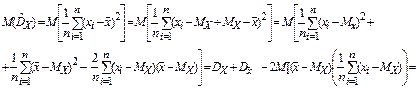
Так как

,

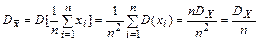то

.

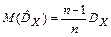Таким образом, замена математического ожидания на среднее арифметическое в выражении (2.30) приводит к смещению оценки дисперсии.

Несмещенную оценку дисперсии получают, домножая 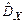на коэффициент 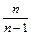, то есть несмещенной оценкой дисперсии является

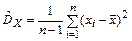. (2.31)

При 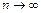коэффициент 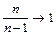, поэтому оценка (2.31) оказывается также состоятельной, как и оценка (2.30).

Оценка среднеквадратического отклонения результата наблюде­ния определяется как правило, по формуле

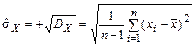. (2.32)

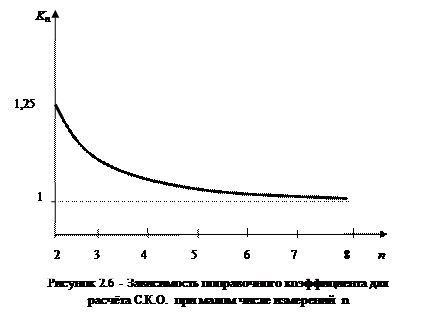
Однако, ввиду нелинейности операции извлечения квадратного корня, такая оценка является смещенной для малого числа наблюдений n , поэтому для устранения этого смещения для 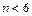применяют выражение

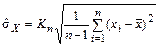(2.33)

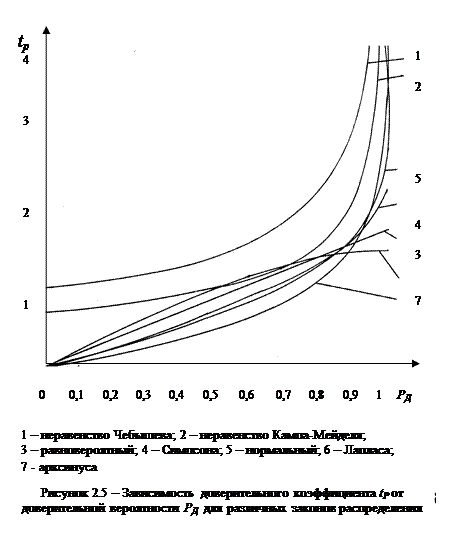
Общий вид этого коэффициента для нормального распределения представлен на рис.2.6 и хорошо апроксимируется выражением

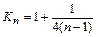. (2.34)

Эффективной называется оценка, обладающая наименьшей диспер­сией (рассеянием) по сравнению с остальными.

Для выбора наиболее эффективной оценки существует целый ряд методов. Наиболее распространенным является метод максимального правдоподобия, теоретически обоснованный Р. Фишером. Идея метода заключается в отыскании таких оценок параметров распределения, при которых достигает максимума т.н. функция правдоподобия. Последняя определяется как вероятность появления всех независимых результатов наблюдения 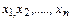. Поскольку вероятность появления результата х_i, лежащего в интервал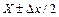е , где 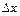- некоторая малая величина, равна 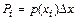, то для независимых результатов наблюдения вероятность появления всего ряда наблюдений 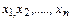есть произведение этих вероятностей

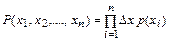. (2.35)

В соответствии с принципом максимального правдоподобия необходимо найти такие оценки параметров дифференциальной функции распределения p(x_i), при которых выражение (2.35) достигает наибольшего значения.

Для упрощения вычислений пользуются логарифмической функцией правдоподобия

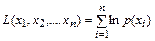. (2.36)

Условие максимума (2.36) получают в результате решения системы уравнений, образуемой при приравнивании нулю производных от (2.36) по тем параметрам, оценки которых мы хотим определить.

Эту задачу можно решить только для конкретного вида дифференциальной функции распределения.

Нормальное распределение.

Плотность распределения

.

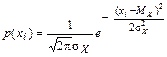Отсюда логарифмическая функция правдоподобия имеет вид

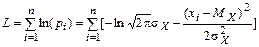. (2.37)

Отыщем наиболее эффективную оценку математического ожидания для нормального распределения

,

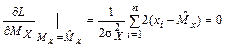то есть .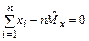

Отсюда 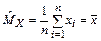. Таким образом, среднее арифметическое является не только состоятельной и несмещенной оценкой математического ожидания, но и для нормального распределения еще и самой эффективной.

Дисперсия среднего арифметического, как уже было показано, равна

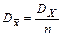(2.38)

То есть дисперсия среднего арифметического в n раз меньше дисперсии результата наблюдения. Для дисперсии

,

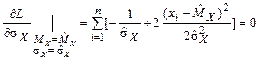откуда 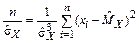и

,

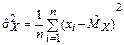то есть для нормального распределения полученная оценка дисперсии является эффективной.