Расчет переходной и импульсной характеристик цепи
Чтобы судить о возможностях электротехнических устройств, принимающих и передающих входные воздействия, прибегают к исследованию их переходных и импульсных характеристик.
Переходная характеристика h(t) линейной цепи, не содержащей независимых источников, численно равна реакции цепи на воздействие единичного скачка тока или напряжения в виде единичной ступенчатой функции 1(t) или 1(t – t0) при нулевых начальных условиях (рис. 14). Размерность переходной характеристики равна отношению размерности реакции к размерности воздействия. Она может быть безразмерной, иметь размерность Ом, Сименс (См).
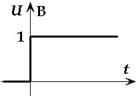
Рис. 14
Импульсная характеристика k(t) линейной цепи, не содержащей независимых источников, численно равна реакции цепи на воздействие единичного импульса в виде d(t) или d(t – t0) функции при нулевых начальных условиях. Ее размерность равна отношению размерности реакции к произведению размерности воздействия на время, поэтому она может иметь размерности с–1, Омс–1, Смс–1.
Импульсную функцию d(t) можно рассматривать как производную единичной ступенчатой функции d(t) = d1(t)/dt. Соответственно, импульсная характеристика всегда является производной по времени от переходной характеристики: k(t) = h(0+)d(t) + dh(t)/dt. Эту связь используют для определения импульсной характеристики. Например, если для некоторой цепи h(t) = 0,7e–100t, то k(t) = 0,7d(t) – 70e–100t. Переходную характеристику можно определить классическим или операторным методом расчета переходных процессов.
Между временными и частотными характеристиками цепи существует связь. Зная операторную передаточную функцию, можно найти изображение реакции цепи: Y(s) = W(s)X(s), т.е. передаточная функция содержит полную информацию о свойствах цепи как системы передачи сигналов от ее входа к выходу при нулевых начальных условиях. При этом характер воздействия и реакции соответствуют тем, для которых определена передаточная функция.
Передаточная функция для линейных цепей не зависит от вида входного воздействия, поэтому она может быть получена из переходной характеристики. Так, при действии на входе единичной ступенчатой функции 1(t) передаточная функция с учетом того, что 1(t) = 1/s, равна
W(s) = L[h(t)] / L[1(t)] = L[h(t)] / (1/s), где L[f(t)] — обозначение прямого преобразования Лапласа над функцией f (t). Переходная характеристика может быть определена через передаточную функцию с помощью обратного преобразования Лапласа, т.е. h(t) = L–1[W(s)(1/s)], где L–1[F(s)] — обозначение обратного преобразования Лапласа над функцией F(s). Таким образом, переходная характеристика h(t) представляет собой функцию, изображение которой равно W(s) /s.
При действии на вход цепи единичной импульсной функции d(t) передаточная функция W(s) = L[k(t)] / L[d(t)] = L[k(t)] / 1 = L[k(t)]. Таким образом, импульсная характеристика цепи k(t) является оригиналом передаточной функции. По известной операторной функции цепи с помощью обратного преобразования Лапласа можно определить импульсную характеристику: k(t) 
W(s). Это означает, что импульсная характеристика цепи единственным образом определяет частотные характеристики цепи и наоборот, так как
W( jw) = W(s)s = jw. Поскольку по известной импульсной характеристике можно найти переходную характеристику цепи (и наоборот), то последняя тоже однозначно определяется частотными характеристиками цепи.
Пример 8. Рассчитать переходную и импульсную характеристики цепи (рис. 15) для входного тока и выходного напряжения при заданных параметрах элементов: R = 50 Ом, L1 = L2 = L = 125 мГн,
С = 80 мкФ.
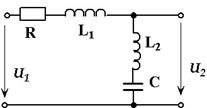
Рис. 15
Решение. Примéним классический метод расчета. Характеристическое уравнение Zвх = R + pL +
+ 1 / (pC) = 0 при заданных параметрах элементов имеет комплексно-сопряженные корни: p1,2 =
= – d jwA2 = – 100 j200, что определяет колебательный характер переходного процесса. В этом случае законы изменения токов и напряжений и их производных в общем виде записывают так:
y(t) = (M сoswA2t + N sinwA2t)e–dt + yвын; dy(t) / dt =
=[(–Md + NwA2) сos wA2t – (MwA2 + Nd)sinwA2t]e–dt + dyвын / dt, где wA2 — частота свободных колебаний; yвын — вынужденная составляющая переходного процесса.
Вначале найдем решение для uC (t) и iC (t) = C duC (t) / dt, воспользовавшись вышеприведенными уравнениями, а затем по уравнениям Кирхгофа определим необходимые напряжения, токи и, соответственно, переходные и импульсные характеристики.
Для определения постоянных интегрирования необходимы начальные и вынужденные значения указанных функций. Их начальные значения известны: uC (0+) = 0 (из определения h(t) и k(t)), так как iC (t) = iL(t) = i(t), то iC (0+) = iL(0+) = 0. Вынужденные значения определим из уравнения, составленного согласно второму закону Кирхгофа для t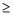 
0+: u1 = R i(t) + (L1 + L2) i(t) / dt + uC(t), u1 = 1(t) = 1 = сonst,
отсюда uC() = uC вын = 1, iC () = iC вын = i() = 0.
Составим уравнения для определения постоянных интегрирования M, N:
uC (0+) = M + uC вын (0+), iC (0+) = С(–Md + NwA2) + iC вын (0+); или: 0 = M + 1; 0 = –M 100 + N 200; отсюда: M = –1, N = –0,5. Полученные значения позволяют записать решения uC(t) и iC (t) = i(t): uC (t) = [–сos200t – -0,5sin200t)e–100t + 1] B, iC (t) = i(t) = [8010–6(100 - 100)Aos200t – (–200 - 50) sin200t)]e–100t] = 0,02
sin200t)e–100t A. Согласно второму закону Кирхгофа,
u2 (t) = uC (t) + uL2 (t), uL2 (t) = uL (t) = Ldi(t) / dt = (0,5сos200t – 0,25sin200t) e–100tB. Тогда u2 (t) =
=(–0,5сos200t – 0,75sin200t) e–100t + 1 = [–0,901sin(200t + 33,69) e–100t + 1] B.
Проверим правильность полученного результата по начальному значению: с одной стороны, u2 (0+) = –0,901 sin (33,69) + 1 = 0,5, а с другой стороны, u2 (0+) = uС (0+) + uL (0+) = 0 + 0,5 — значения совпадают.
Определим переходные и импульсные характеристики схемы: hi (t) = i(t) / u1(t) = i(t) / (1 B) = 0,02 sin200t e–100t См; ki (t) = hi(0+) d(t) + dhi (t) / dt = (4 сos200t – 2 sin200t) e–100t См/с; hu2 (t) =
= u2(t) / u1(t) = u2 (t) / (1 B) = [–0,901sin(200t + 33,69) e–100t + 1] б/р, ku2 (t) = hu2 (0+) d(t) + dhu2 (t) / dt = 0,5d(t) + (–180,2 сos200t + 90,1 sin200t) e–100t с–1.