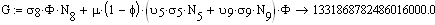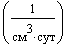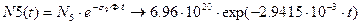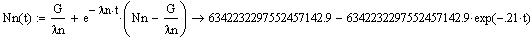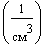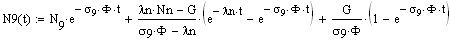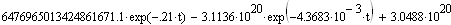Численное определение концентраций нуклидов

Основные цели работы

1) по вербальной постановке задачи составить математическую модель изменения концентрации нуклидов;

2) разрешить полученную систему дифференциальных уравнений одним из известных способов, то есть получить аналитическое решение;

3) используя имеющиеся численные данные, определить необходимые характеристики процесса;

4) дать графическую интерпретацию решений и сделать заключение по работе.

2. Вербальная постановка задачи

Нуклидный состав уранового топлива в реакторе на тепловых нейтронах изменяется в результате следующих процессов:

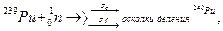
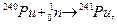
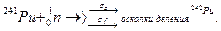
Полагая, что поток нейтронов, 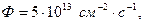т.е. не зависит от времени, оценить изменение изотопного состава топлива в течение двух недель с начала работы свежего реактора (модель “малого выгорания”).

Математическая модель процесса

Математическую постановку задачи представляем в виде:

При радиационном захвате нейтрона ядром 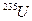образуется 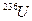, а поскольку сечение 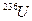мало, его влиянием на реактивность при малых глубинах выгорания можно пренебречь. В цепочке превращений, начинающейся с 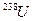, пренебрегаем 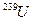, поскольку его период полураспада мал. 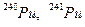мы так же пренебрегаем, т.к. изменение их концентраций за малый промежуток времени, который мы рассматриваем, пренебрежимо мало.

Таким образом, математическая постановка задачи может быть представлена следующей системой уравнений:

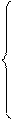
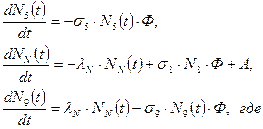(2)

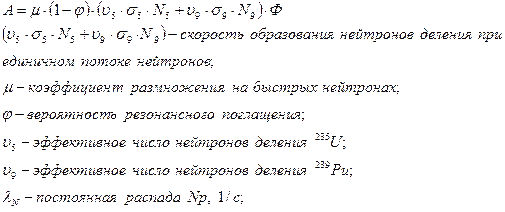
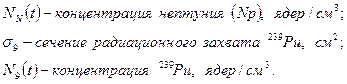
Аналитическое решение системы уравнений

Решим систему уравнений (2), воспользовавшись допущениями, приведенными в предыдущем пункте.

Первое уравнение решим методом разделения переменных.

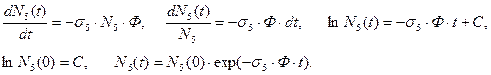
Для решения второго и третьего уравнений воспользуемся методом “выделения интегрирующего множителя”.

Введем дополнительное обозначение для второго уравнения, которое позволит нам избежать громоздких выражений: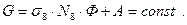

Данный метод дает общее решение неоднородного дифференциального уравнения 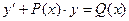, имеющее вид:

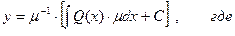
Таким образом, записав в нужном виде второе уравнение системы (2), проделав необходимые преобразования и вычисления, решением второго уравнения будет следующее равенство:

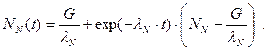
Чтобы решить третье уравнение системы (1), необходимо учесть решение предыдущего уравнения. Здесь будем иметь следующее:

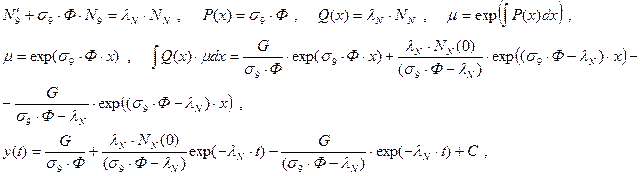
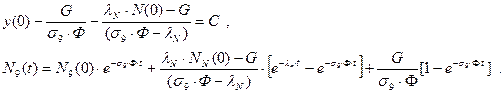
Численное определение концентраций нуклидов

Зададимся численными значениями характеристик. Из [2] в приложениях берем значения следующих величин:

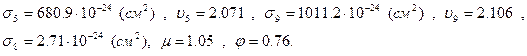
Из условия задачи находим

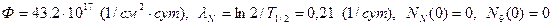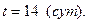, Концентраци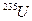и и 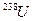рассчитаем, зная что в окиси содержится 3% 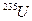( 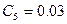), а плотность 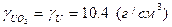. Концентрацию окиси обозначим 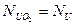. Тогда получаем следующее:

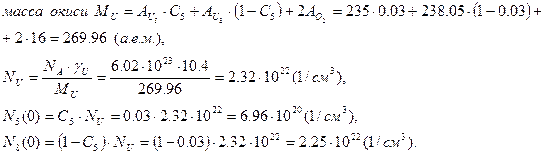
Используя выше приведенные данные, получим численные решения системы уравнений (1).