Теоремы умножения вероятностей
Вероятность события А, вычисления в предположении, что событие В уже произошло 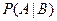 , называется условной вероятностью.
, называется условной вероятностью.
V В урне (J обобщенное название любой непрозрачной емкости с любыми одинаковыми на ощупь предметами) находятся 3 белых и 3 черных шара. Из урны вынимают по одному шару без возвращения. Найти вероятность появления белого шара при втором испытании, если первый извлеченный шар был черным.
Ï Событие В – первый вытащен черный шар.
Событие А – вторым вытащен белый.
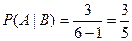 N
N
Понятие условной вероятности играет важнейшую роль в современной теории вероятностей и математической статистике. Условная вероятность позволяет учитывать дополнительную информацию о событиях.
Формула для определения условной вероятности:
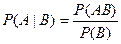
Доказательство:
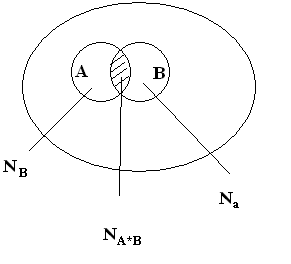 | 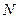 -общее число элементарных исходов -общее число элементарных исходов 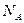 - число исходов, благоприятствующих А - число исходов, благоприятствующих А 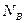 - число исходов, благоприятствующих В - число исходов, благоприятствующих В 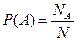 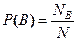 |
Нам известно, что событие В уже произошло (т.е. число возможных исходов сократилось до тех, которые благоприятствуют событию В). Теперь, при определении вероятности события А нам нужно выбирать из 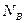 возможных исходов. Причем, среди них событию А благоприятствуют
возможных исходов. Причем, среди них событию А благоприятствуют 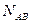 исходов, при которых происходит и А и В. Тогда
исходов, при которых происходит и А и В. Тогда
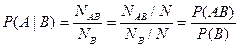
При выводе мы осуществили переход к новому пространству элементарных исходов ( 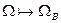 ).<
).<
Условной вероятностью события А при условии события В называется отношение вероятности произведения событий А и В к вероятности события В:
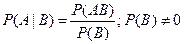 .
.
V Испытание: бросание кости.
Событие В: выпадение 4 или 6 очков.
Событие А1 : выпадение четного числа очков.
Событие А2 : выпадение 3, 4 или 5 очков.
Событие А3 : выпадение нечетного числа очков.
Найти условные вероятности 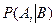
Ï 1. А1*В=В 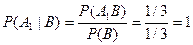
2. 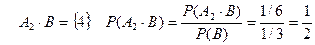
3. 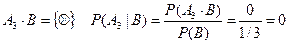 N
N
Рассмотрим два события А и В. Пусть известны 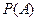 и
и 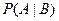 . Как найти вероятность совместного появления события А и В -
. Как найти вероятность совместного появления события А и В - 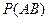 ?
?
Теорема. Вероятность совместного появления 2-х событий равна произведению вероятности одного из них на условную вероятность другого, вычисленную в предположении, что первое событие произошло:
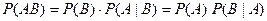 .
.
Доказательство: смотри определение условной вероятности. <
Следствие. Вероятность совместимого появления нескольких событий равна произведению вероятности одного из них на условные вероятности всех остальных, причем вероятность каждого последующего события вычисляется в предположении, что все предыдущие события уже произошли:
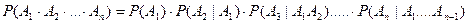 .
.
Порядок нумерации событий значения не имеет.
V В урне находятся 5 белых, 4 черных и 3синих шара.
Испытание: извлекают шар, смотрят и откладывают в сторону (выборка без возврата). Найти вероятность того, что первый извлеченный шар был белым, второй – черным, третий – синим.
Ï Пусть событие А: 1-й шар – белый, В: 2-й шар –черный, С: 3-й шар – синий.
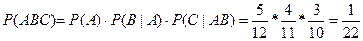 . N
. N
НЕЗАВИСИМЫЕ И ЗАВИСИМЫЕ СОБЫТИЯ
Рассмотрим два события А и В. Вероятность 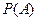 назовем безусловной, а вероятность
назовем безусловной, а вероятность 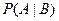 соответственно условной. Наступление события В может влиять или не влиять на вероятность события А, т.е.
соответственно условной. Наступление события В может влиять или не влиять на вероятность события А, т.е. 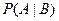 может быть равна
может быть равна 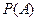 , а может и нет.
, а может и нет.
События А и В, имеющие ненулевые вероятности, называются независимыми, если 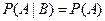 или
или 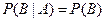 .
.
В противном случае события А и В называются зависимыми. Свойство независимости взаимно.
Теорема умножения вероятностей для независимых событий: 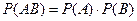
Доказательство:
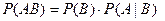 ,т.к.события независимы, то
,т.к.события независимы, то 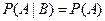 и
и 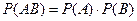 <
<
Два события называются независимыми, если вероятность их произведения равна произведению их вероятностей:

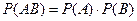
На практике о независимости событий судят по смыслу задачи. Например, если говорится о том, что стреляют два стрелка, то события «попал 1-й стрелок» и «попал 2-й стрелок» считаются независимыми (J конечно, если стрелки стреляют по мишени, а не друг в друга).
V Найти вероятность попадания в мишень обоими лучниками, если вероятность попадания 1-го равна 0.5, а 2-го -0.8?
Ï Пусть событие А: попал 1-й стрелок, событие В: попал 2-й стрелок. Тогда событие АВ – попал и 1-й и 2-й лучник.
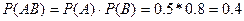 N
N
Несколько событий называются попарно независимыми, если независимы каждые два из них.
Введем понятие независимости в совокупности.
События называются независимыми в совокупности, если вероятность произведения любых двух событий равна произведению вероятностей этих событий; вероятность произведения любых трех событий равна произведению вероятностей этих событий; … ; вероятность произведения любых n событий равна произведению вероятностей этих событий:
События 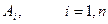
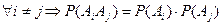
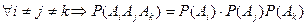
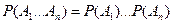 .
.
Из независимости событий в совокупности следует их попарная независимость, но не наоборот.
