Трехпроводная схема включения ТС

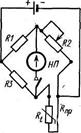
Рис. 6.7. Трехпроводная система включения термометра сопротивления в измерительный мост

В случаях, когда колебания температуры среды, окружающей соединительные провода, значительны и погрешность при измерении может превысить допустимую величину, применяют трехпроводную систему проводки, которая состоит в том, что одну из вершин моста переносят непосредственно к головке термометра (рис. 6.7). При таком присоединении сопротивление одного про­вода Rпp прибавляется к сопротивлению Rt, а сопротивление второго провода — к сопротивлению КПР R2, уравнение равновесия моста принимает вид R_t + R_пр = (R₂ + R_пр) R₃/R₁.

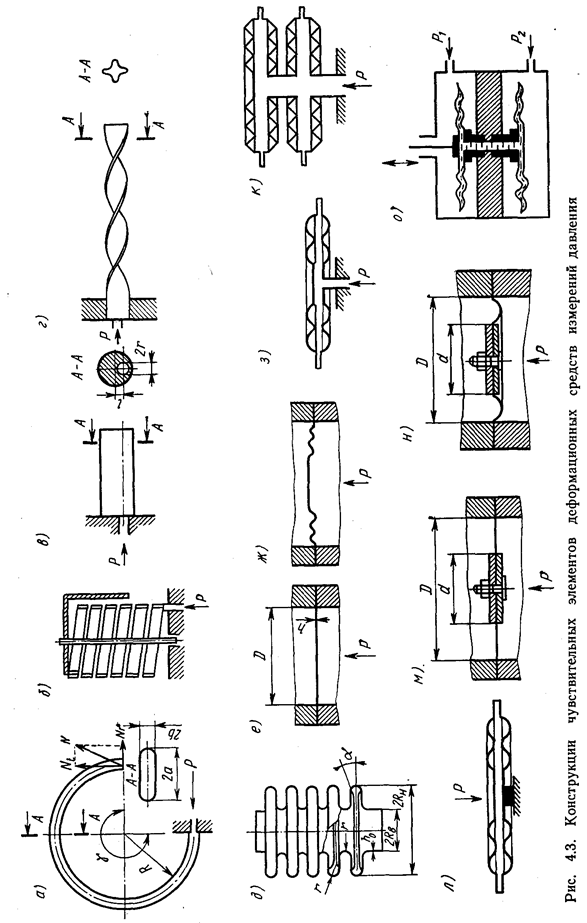
В автоматических уравновешенных мостах (рис. 6.8) движок КПР перемещается автоматически, а не вручную.

Измерительная схема уравновешенных мостов питается как постоянным, так и переменным током. В автоматических мостах переменного тока решающее влияние имеют активные сопротив­ления, поэтому выведенные выше соотношения для мостов постоян­ного тока сохраняются и для автоматических мостов переменного тока. Последние имеют ряд преимуществ перед мостами постоянного тока: измерительная схема питается от одной из обмоток силового трансформатора электронного усилителя, т. е. не требу­ется дополнительного источника питания (сухого элемента) и отпадает необходимость в применении вибрационного преобразо­вателя.

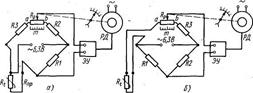
Рис. 6.8. Принципиальные схемы автоматического уравновешенного моста на переменном токе

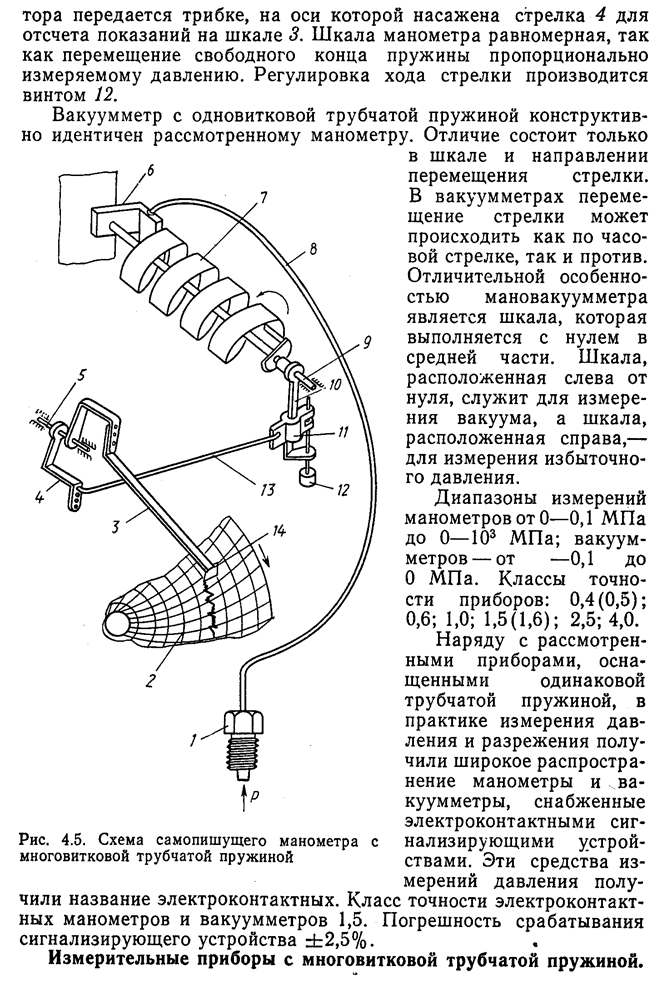
Неуравновешенные мосты.

Возможность непосредственного отсчета температуры — преимущество неуравновешенного моста перед лабораторным уравновешенным мостом. На рис. при­ведена схема неуравновешенного моста, в которой R1, R2 и R3 — постоянные резисторы плеч моста; R — реостат; R_K — контроль­ный резистор; R_t — сопротивление термометра; Iм — сила тока, протекающего по рамке милливольтметра.

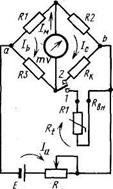
Для определения сил токов в плечах моста воспользуемся методом контурных токов. Принимая ЭДС источника питания постоянной, рассмотрим три контура с силами тока I_а, I_b, Iс. Для них можно записать следующие уравнения:

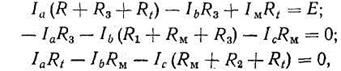(6.12)

Подставим в уравнение :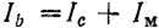

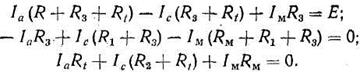(6.13)

Решив эти уравнения, найдем

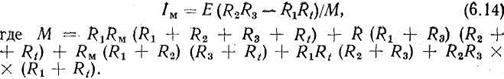
Аналогично определим силу тока в плечах моста:

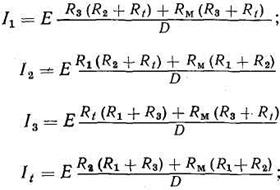
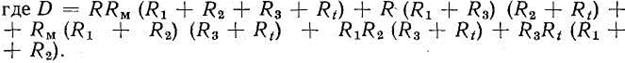
Из уравнения (6.14) видно, что сила тока зависит от Е или разности потенциалов на вершинах моста. Следовательно,

Необходимым условием правильного измерения является поддер­жание разности потенциалов постоянной, для чего в цепь источ­ника тока вводят регулировочный реостат R.

Для контроля разности потенциалов в схему моста параллельно термометру включают манганиновый контрольный резистор RK, сопротивление которого равно сопротивлению термометра при определенной температуре, отмеченной красной чертой на шкале милливольтметра.

Для контроля разности потенциалов Uab переключатель ставят в положение 2 и реостатом R устанавливают стрелку милливольтметра точно на красной черте. После этого переключатель ставят в положение 1 и по шкале снимают показания, соответству­ющие температуре термометра. Неуравновешенные мосты питаются от батареи или от сети (через трансформатор и выпрямитель).

Показания неуравновешенных мостов зависят от напряжения Uab, поэтому их не используют для промышленных измерений. Эти мосты применяют иногда в лабораторной практике, а также используют в измерительных схемах других приборов (логометров, газоанализаторов и т.п.).

ВОПРОС №16

ВОПРОС №17

ВОПРОС №18

ВОПРОС №19

ВОПРОС №20

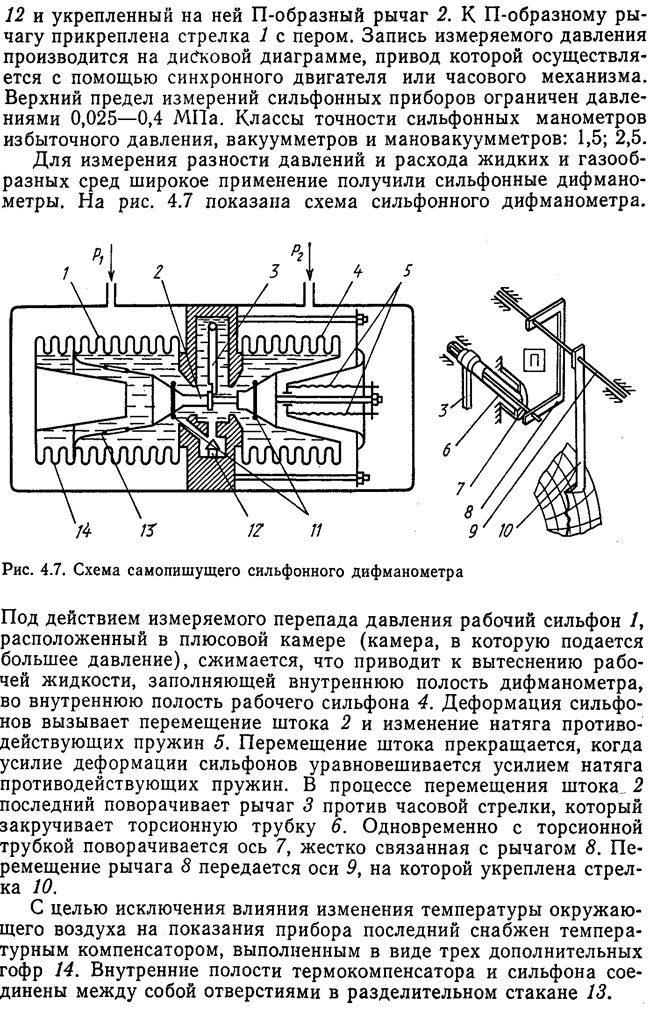
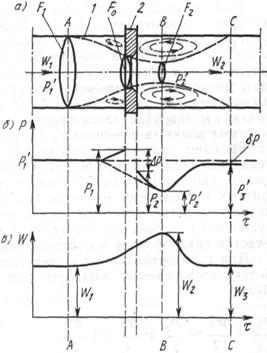Течение вещества через диафрагму (а) и эпюры давления (б) и скорости (в)

В соответствии с рассматриваемым принципом в трубопровод устанавливают сужающее устройство. При протекании измеряемого потока через отверстие сужающего устройства увеличивается скорость потока по сравнению с его скоростью до сужения. Благодаря этому давление потока на выходе из сужающего устройства уменьшается и на сужающем устройстве создается перепад давления, измеряемый дифманометром, который, как будет показано ниже, зависит от скорости в сужении или от расхода потока.

Выделим в трубопроводе три сечения: А-А — перед сужающим устройством, где еще нет его влияния на поток; В-В — место наибольшего сужения струи; С-С— сечение после сужающего устройства, где устанавливаются скорость и давление потока.

Пройдя сечение А-А, поток сжимается, и благодаря действию сил инерции сжатие продолжается и на выходе из диафрагмы достигает наибольшего значения на некотором расстоянии за ней (сечение В-В). Уменьшение сечения струи приводит к увеличению скорости от W'i в сечении А-А до W₂ в сечении В-В. Что касается давления, то здесь необходимо различать давление у стенки трубы и на ее оси. Как видно из графика (рис. 7.5,6), давление в одной и той же плоскости неравномерно. Давление у стенки трубы (сплошная линия) непосредственно перед диафрагмой Р\ несколько возрастает (за счет уменьшения скорости в этом месте), а по оси трубы (штрихпунктирная линия) уменьшается и достигает минимума рч' в сечении В-В. Далее, по мере расширения потока, скорость потока уменьшается, а давление у стенки трубы возрастает, и в сечении С-С эти значения устанавливаются.

Изменение давления струи по оси трубопровода практически совпадает с изменением давления около его стенки, за исключением участка перед диафрагмой и непосредственно в ней. Однако если скорость потока W₃ в сечении С-С в идеальном случае равна скорости Wi до сужения, т. е. в сечении А-А, то давление Р₃' в сечении С-С не достигает прежнего значения на величину ЬР=Р\—/Y, называемую безвозвратной потерей давления. Эта потеря давления связана с затратой части энергии потока на вихреобразования в мертвых зонах (в основном за диафрагмой) и на трение.

Выведем уравнение расхода для несжимаемой жидкости, протекающей через диафрагму. При этом примем следующие предпосылки: движение жидкости установившееся, поток однороден и его фазовое состояние не меняется при прохождении через диафрагму, поток полностью заполняет все сечение трубопровода до и после сужающего устройства, отсутствуют возмущения потока, а прямые участки трубопровода достаточно велики.

Для горизонтального участка трубопровода уравнение энергии потока несжимаемой жидкости для сечений А-А и В-В будет

(7.12)

где Р₁’ и Р₂’ —абсолютные статические давления соответственно в сечениях А-А и В-В;

W₁ и W₂ — скорости потока соответственно в сечениях А-А и В-В;

ρ — плотность жидкости;

ξ — коэффициент гидравлических потерь;

ξ 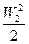— потеря энергии на трение на участке А-А—В-В.

Согласно уравнению неразрывности струи

F₁W₁=F₂W₂ (7.13)

где F₁ и F₂ — площади поперечного сечения потока соответственно в сечениях А-А и В-В.

Введем следующие обозначения:

F₀/F₁=d²/D²=m (7.14)

F₂/F₀=μ (7.15)

где F₀ и d — площадь и диаметр входного отверстия сужающего устройства; D — диаметр трубопровода; m — относительная площадь (модуль) сужающего устройства;μ — коэффициент сужения струи. Из уравнения (7.13) и выражений (7.14) и (7.15) имеем

W₁ = μmW₂. (7.16)

Подставляя это значение W₁ в уравнение (7.12), определим скорость потока в месте наибольшего сужения:

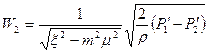(7.17)

Обычно перепад давления измеряют не в сечениях А-А и В-В (т. е. не Р₁’– Р₂’), а непосредственно до и после сужающего устройства, а именно ΔР=Р₁—Р₂. Соотношение между указанными перепадами устанавливается с помощью поправочного коэффициента ψ, т. е.

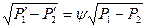(7.18)

Тогда уравнение (7.17) примет вид

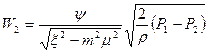(7.19)

Массовый расход вещества

G=W₂F₂ρ= W₂μF₀ρ

Подставляя сюда W₂ из выражения (7.19), получим

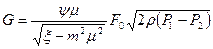(7.20)

Коэффициенты μ и ψ не могут быть определены независимо друг от друга. Исходя из этого, их объединяют в один экспериментально определяемый комплексный коэффициент α, называемый коэффициентом расхода:

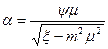(7.21)

Таким образом, учитывая выражения (7.20) и (7.21) и принимая во внимание, что F₀=πd²/4, получим уравнения для массового G и объемного Q расходов несжимаемой жидкости:

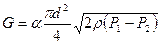(7.22) 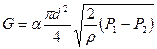(7.23)

Если через сужающее устройство протекает сжимаемая среда (газ или пар), то вследствие понижения давления увеличивается ее объем. Это приводит к тому, что скорость потока возрастает и становится больше скорости несжимаемой среды. В результате на сужающем устройстве увеличивается перепад давления.

Учет указанного явления производится введением в уравнения расходов (7.22) и (7.23) дополнительного коэффициента ε<1, называемого поправочным множителем на расширение измеряемой среды.

Тогда уравнения для массового G и объемного Q расходов сжимаемой среды запишем в виде:

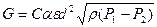(7.24) 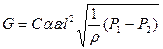(7.25)

где 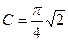—постоянный коэффициент; ρ — плотность среды в рабочих условиях на входе в сужающее устройство, т. е. при давлении Р₁ и температуре Т₁ перед сужающим устройством.

Уравнения (7.24) и (7.25) являются основными уравнениями расхода как для сжимаемых, так и несжимаемых сред, при этом для последних ε =1. Использование уравнений (7.24) и (7.25) возможно только при условии, что скорость газа или пара меньше критической скорости.

Проанализируем величины, входящие в уравнения (7.24) и (7.25), и зависимость их от параметров измеряемого потока.

Коэффициент С не зависит от параметров измеряемого потока, он зависит от выбора единиц измерения, типа используемого дифманометра, а также от плотности сред, заполняющих импульсные трубки, соединяющие сужающее устройство с дифманометром.

Коэффициент расхода α, выражаемый формулой (7.21), не может быть пока точно рассчитан теоретическим путем. Значения этого коэффициента для некоторых типов сужающих устройств определены экспериментально.

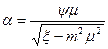(7.21)

Поправочный множитель на расширение измеряемой среды ε вводится в уравнение расхода при измерении расхода газа и паров и учитывает изменение их плотности при протекании через сужающее устройство. Для несжимаемых жидкостей е=1. В общем случае поправочный множитель ε представляется в виде

ε =f(ΔP/P₁,m,χ) (7.30)

где ΔP/P₁ — отношение перепада давления к давлению до сужающего устройства; χ — показатель политропы измеряемой среды, m – модуль сужающего устройства.

Диаметры трубопровода D и сужающего устройства d должны быть учтены в уравнении расхода при рабочей температуре t. Соотношение их с соответствующими диаметрами при температуре 20°С, т. е. D₂₀ и d₂₀, определяется выражениями:

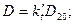
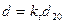
где k_t' и k_t — поправочные множители на тепловое расширение материала трубопровода и сужающего устройства. При температуре от – 20 до +60°С можно принять k_t'=k_t=l.

Плотность измеряемой среды ρ, определяется по состоянию потока в рабочих условиях до сужающего устройства. Если известна плотность жидкости при температуре 20°С—t₂₀, то плотность ρ при рабочей температуре t₁ определяют по формуле

ρ= ρ₂₀[1–β(t₁–20)] (7.33)

где ρ — средний коэффициент объемного расширения жидкости в интервале t₂₀— t₁.

Перепад давления ΔР является одним из основных параметров, характеризующих расход вещества, и измеряется дифманометром.

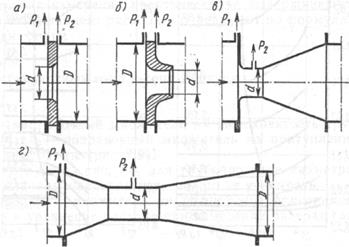
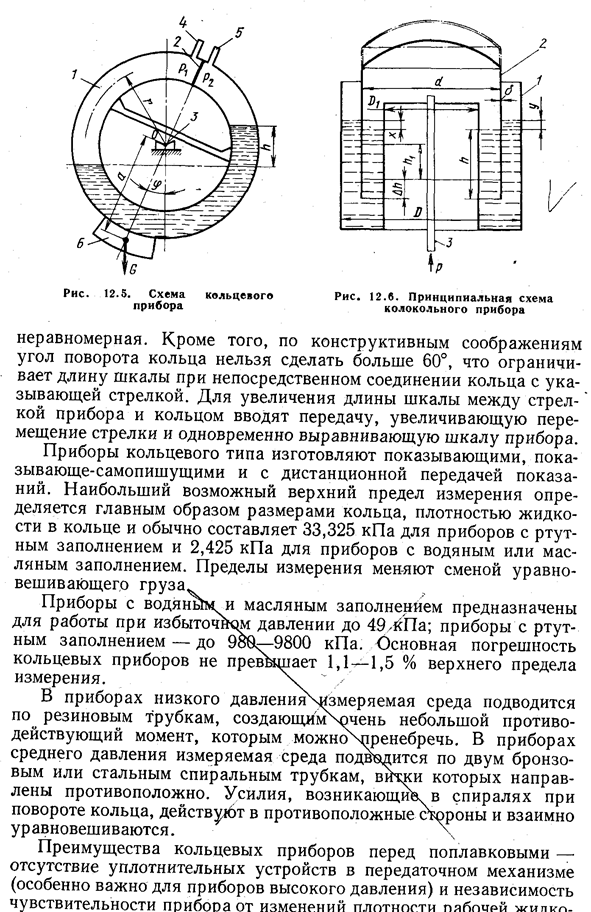
Рис. 7.6. Схемы стандартных сужающих устройств

Кроме диафрагмы (рис. 7.6, а) в дроссельных расходомерах в качестве сужающих устройств находят применение стандартные сопла (рис. 7.6,6), сопла Вентури (рис. 7.6, в) и трубы Вентури (рис. 7.6, г). На рис. 7.6 показаны места отбора давлений Р\ и Р₂ от сужающих устройств к дифманометру. Характерной особенностью сужающих устройств (рис. 7.6, б, в, г) является меньшая, чем для диафрагмы, безвозвратная потеря давления при одном и том же значении модуля т сужающего устройства.

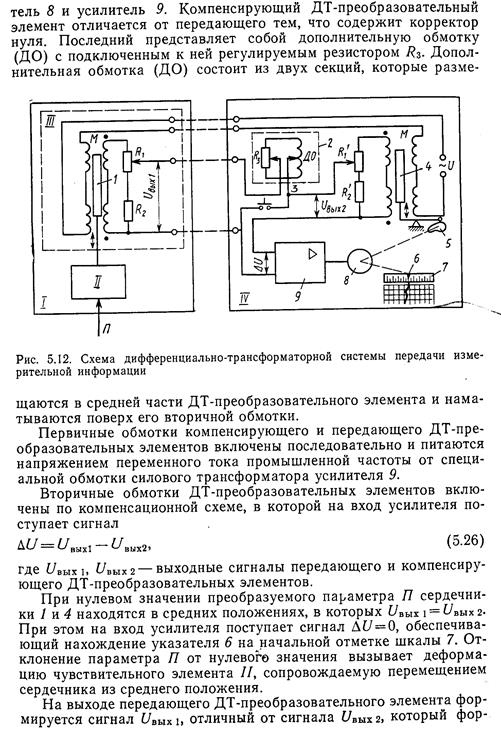
Стандартная диафрагма наиболее простое и распространенное сужающее устр-во. Ее применяют без индивидуальной градуировки для трубопроводов D>>50 мм при условии, что 0.05≤m≤0.7.Диафрагма предст. собой тонкий диск с круглым концентрическим отверстием (рис.18.11) которое имеет со стороны входа острую цилиндрическую кромку, а далее расточено под углом φ=30…45⁰.Входная кромка диафрагмы не должна иметь закруглений, вмятин, зазубрин, заусенцев. Толщина диафрагмы Е не должна превышать 0,05D₂₀ D₂₀-диаметр трубопровода при температуре 20⁰С).длина цилиндр. отверстия должна быть в пределах 0,005D₂₀≤e≤0.02D₂₀.У диафрагм толщиной более 0,02D₂₀ цилиндр. отверстие должно переходить в коническую выходную часть. Отклонение диаметра отверстия от среднего значения, определенное не менее чем в четырех равноотстоящих одно от другого диаметральных направлениях, не должно превышать 0,05%.Наиболее подходящие материалы для изготовления диафрагмы это стали 12Х17(для среды с температурой до 400⁰С) и 12Х18Н9Т(выше 400⁰С).При измерении расхода агрессивных жидкостей и газов следует применять кислотоупорные и жаростойкие стали различных марок, эбонит, сплав свинца с сурьмой. Измерение перепада давлений в сужающем устр-ве обычно выполняют через отдельные цилиндрические отверстия(рис.18.11-нижняя часть-А) или через две кольцевые камеры, каждая из которых соединяется с внутр. полостью трубопровода кольцевой щелью (рис.18.11 верхняя часть-Б).Кольцевые камеры обеспечивают выравнивание давлений при небольших прямых участках трубопровода до и после диафрагмы. При небольших давлениях в трубопроводах более 400 мм кольцевая камера может быть образована полостью трубки, согнутой вокруг трубопровода в кольцо или прямоугольник. При этом число отверстий соединяющих камеру с полостью трубопровода должно быть не менее 4.Размер с(ширина кольцевой щели соедин. камеру с трубопроводом) при m≤0.45 не должен превышать 0,03D₂₀ а при m>0.45 должен быть в пределе 0,01D₂₀≤c≤0.02D₂₀.Одновременно должны соблюдаться след. условия: для чистых газов и жидкостей 1 мм≤с≤10 мм; для паров, влажных газов и жидкостей которые могут испаряться в соединит. линиях при измерении перепада давлений через отд.отверстия 4мм≤с≤10мм через камеры 1мм≤с≤10 мм.

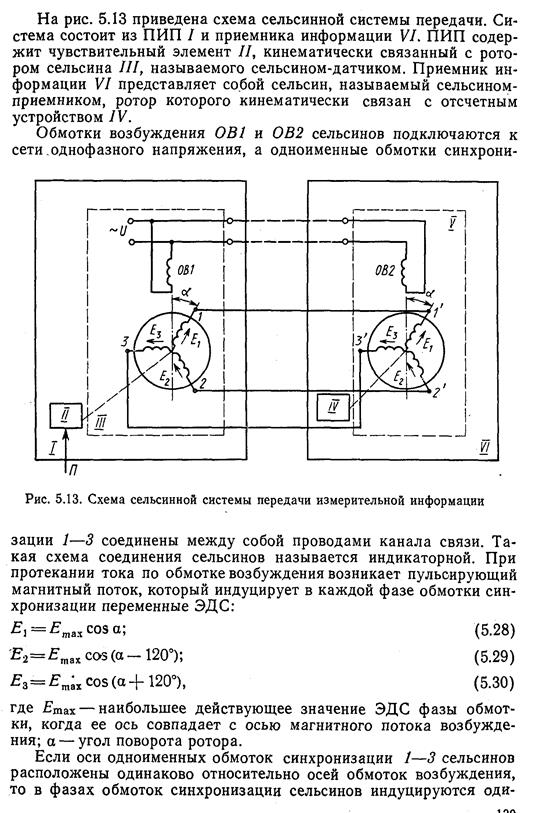
Стандартные сопла можно применять без дополнительной градуировки в трубопроводах D≥50мм при условии, что 0,05≤m≤0,65 (рис.18.13 и 18.14).

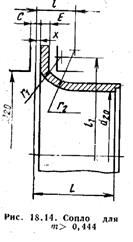
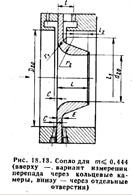Профильная часть отверстия сопла должна быть выполнена с плавным сопряжением дуг. Поверхность входной части сопла не должна быть шероховатой; для цилиндр. части исключается конусность. Выходная кромка цилиндр. части отверстия должна быть острой, без заусенцев, фаски или закругления. Для изготовления сопел обычно применяют те же материалы что и для диафрагм. Размер с принимают по тем же условиям что и для диафрагм. На выходе цилиндр. часть отверстия сопла должна оканчиваться расточкой предохраняющей выходную кромку от повреждений. Сопла особенно удобны при измерении расхода газов и перегретого пара если ∆р/р₁≤0,1, а также при измерении расхода пара высокого давления в трубопроводах диаметром D≤200мм.По сравнению с диафрагмами сопла менее чувствительны к коррозии, загрязнениям и обеспечивают несколько большую точность измерения. Сопла Вентури можно применять без индивидуальной градуировки для трубопроводов D≥50мм при одновременном соблюдении условия 0,05≤m≤0,6.Профильную входную часть сопел Вентури выполняют такой же, как у обычного сопла(для m≤0.44 по рис.18.13 для m≥0,44 по рис.18.14).Цилиндр. средняя часть без сопряжения переходит в конус. Сопла Вентури могут быть длинными и короткими. Наибольший диаметр выходного конуса у длинного сопла Вентури равен диаметру трубопровода, а у короткого - меньше диаметра трубопровода. Перепад давлений измеряют через кольцевые камеры, причем задняя камера соединяется с цилиндр. частью сопла Вентури радикальными отверстиями, диаметр которых должен быть не более 0,13d₂₀ но не менее 3мм.Короткие сопла получили большее применение, так как дешевле в изготовлении и монтаже, а потеря давления в них такая же как и у длинных. Потеря давления в сопле Вентури возрастает с увеличением угла φ и уменьшением длины конуса. Исследует применять когда потеря давления имеет решающее значение.

ВОПРОС №21

Рассмотренный способ измерения одинарной напорной трубкой, дальнейшее развитие привело к созданию двойных трубок. Напорными трубками полное и статическое давление измеряют с некоторой погрешностью. Отверстия для всех трубок не одинаковы, поэтому вводят поправочный коэффициент ξ.

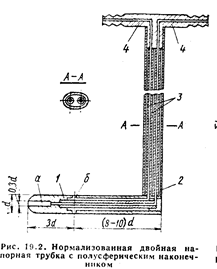
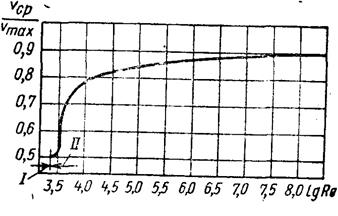
ВОПРОС №22

ВОПРОС №23

ВОПРОС №24

ВОПРОС №25