Нестационарное уравнение Шредингера.

Лекция 5. УРАВНЕНИЕ ШРЕДИНГЕРА.

Вероятностный смысл волн де Бройля. Волновая функция.

Волны де Бройля имеют специфическую квантовую природу, не имеющую аналогии с волнами в классической физике. Это не электромагнитные волны, так как их распространение в пространстве не связано с распространением какого-либо электромагнитного поля. Вопрос о природе волн можно сформулировать как вопрос о физическом смысле амплитуды этих волн. Вместо амплитуды удобнее выбрать интенсивность волны, пропорциональную квадрату модуля амплитуды.

Из опытов по дифракции электронов следует, что в этих экспериментах обнаруживается неодинаковое распределение пучков электронов, отраженных по различным направлениям. С волновой точки зрения наличие максимумов числа электронов в некоторых направлениях означает, что эти направления соответствуют наибольшей интенсивности волн де Бройля. Интенсивность волн в данной точке пространства определяет плотность вероятности попадания электронов в эту точку за 1 сек.

Это послужило основанием для своеобразного статистического, вероятностного истолкования волн де Бройля.

Квадрат модуля амплитуды волн де Бройля в данной точке является мерой вероятности того, что частица обнаруживается в этой точке.

Для того чтобы описать распределение вероятности нахождения частицы в данный момент времени в некоторой точке пространства, введем функцию, которая является функцией времени и координат, обозначается греческой буквой ψ и называется волновой функцией или просто пси-функцией.

По определению 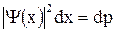- вероятность того, что частица имеет координату в пределах x, x+dx.

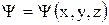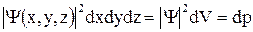Если , то - вероятность того, что частица находится в объеме dxdydz.

Следовательно, вероятность того, что частица находится в элементе объема dV, пропорциональна квадрату модуля пси-функции и элементу объема dV.

Физический смысл имеет не сама функция ψ, а квадрат ее модуля 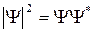, где ψ* - функция, комплексно сопряженная с ψ. Величина 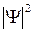имеет смысл плотности вероятности, т.е. определяет вероятность пребывания частицы в данной точке пространства. Иными словами определяет интенсивность волн де Бройля. Волновая функция является основной характеристикой состояния микрообъектов (элементарных частиц, атомов, молекул).

Нестационарное уравнение Шредингера.

Уравнения Ньютона в классической механике позволяют для макроскопических тел решить основную задачу механики – по заданным силам, действующим на тело (или систему тел), и начальным условиям найти для любого момента времени координаты тела и его скорость, т.е. описать движение тела в пространстве и времени.

При постановке аналогичной задачи в квантовой механике необходимо учитывать ограничения на возможность применения к микрочастицам классических понятий координат и импульса. Поскольку состояние микрочастицы в пространстве в данный момент времени задается волновой функцией, а точнее 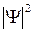- вероятностью нахождения частицы в точке x,y,z в момент t , основное уравнение квантовой механики является уравнением относительно пси-функции .

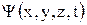Это уравнение было получено в 1926 г. Шредингером. Как и уравнения движения Ньютона, уравнение Шредингера постулируется, а не выводится. Справедливость этого уравнения доказывается тем, что полученные с его помощью выводы находятся в хорошем согласии с экспериментами.

Уравнение Шредингера имеет вид

,

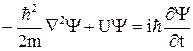здесь m – масса частицы, i – мнимая единица, 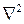- оператор Лапласа, результат действия которого на некоторую функцию

.

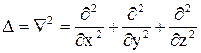U(x,y,z,t) – в рамках наших задач потенциальная энергия частицы, движущейся в силовом поле. Из уравнения Шредингера следует, что вид пси-функции определяется функцией U, т.е. в конечном счете, характером сил, действующих на частицу.

Уравнение Шредингера дополняется важными условиями, которые накладываются на пси-функцию. Этих условий три:

1) функция ψ должна быть конечной, непрерывной и однозначной;

2) производные 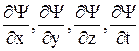должны быть непрерывны

3) функция 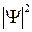должна быть интегрируема, т.е. интеграл

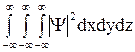
должен быть конечным. В простейших случаях третье условие сводится к условию нормировки

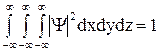
Это означает, что пребывание частицы где-либо в пространстве есть достоверное событие и его вероятность должна быть равна единице. Первые два условия – обычные требования, накладываемые на искомое решение дифференциального уравнения.

Поясним, как можно прийти к уравнению Шредингера. Ограничимся для простоты одномерным случаем. Рассмотрим свободно движущуюся частицу (U = 0).

Сопоставим ей, согласно идее де Бройля, плоскую волну

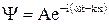
Заменим 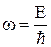и 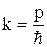и перепишем

.

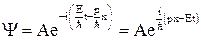Продифференцировав это выражение один раз по t, а второй раз дважды по x, получим

;

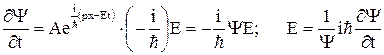
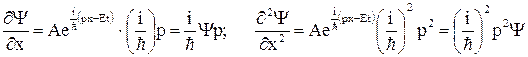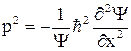
Энергия и импульс свободной частицы связаны соотношением

.

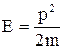Подставив в это соотношения выражения для Е и р²

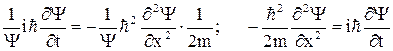
Последнее выражение совпадает с уравнением Шредингера при U =0.

В случае движения частицы в силовом поле, характеризуемом потенциальной энергией U, энергия Е и импульс р связаны соотношением

.

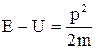Тогда

.

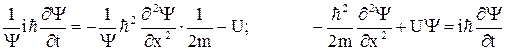Изложенные рассуждения не имеют доказательной силы и не могут рассматриваться как вывод уравнения Шредингера. Их цель – пояснить, каким образом можно прийти к установлению этого уравнения.