Эпюры гидростатического давления

На криволинейные поверхности

Первый случай. Цилиндрическая поверхность, давление жидкости с одной стороны – справа (рис 2.25).

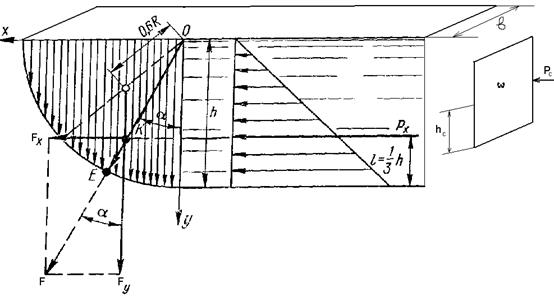
Рис.2.25

1) Выберем оси координат ОУ.

2)Определим горизонтальную (спроектируем) составляющую суммарного гидростатического давления. Она равна произведению силы гидростатического давления на площадь сечения, т.е.

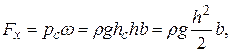
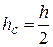, т.к. 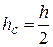. (2.111)

3) Плечо давления горизонтальной составляющей силы

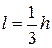, (2.112)

4)Определим вертикальную составляющую суммарного гидростатического давления.

Поскольку силу давления жидкости на стенку можно вычислить так же по объёму эпюры, принимая последнюю за нагрузку, приложенную к стенке, то запишем

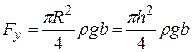. (2.113)

5) Определим равнодействующую

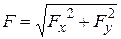. (2.114)

6) Найдём угол наклона линии действия силы F

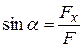. (2.115)

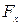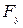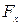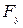7) Графическим способом определим точку приложения силы F. Для этого проводим линию по направлению до пересечения с вертикальной составляющей силой , приложенной в центре тяжести тела давления. От точки пересечения сил и строим параллелограмм и находим равнодействующую силы F. Далее величину F откладываем в масштабе на линии равнодействующей от криволинейной поверхности – точка Е, которая и есть точка приложения равнодействующей силы – центр давления.

Второй случай. Цилиндрическая поверхность, давление жидкости слева. Все расчёты и графическое определение центра давления производятся как и в первом случае (вместо - ).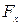

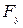Третий и четвёртый случаи построения эпюр гидростатического давления на криволинейные поверхности можно изучить по [ ].

Закон Архимеда

Закон Архимеда о силе, действующей на погруженное в воду тело был сформулирован Архимедом за 250 лет до н.э. В настоящее время он звучит следующим образом: на погруженное в жидкость тело действует выталкивающая сила, равная весу жидкости, вытесненной этим телом.

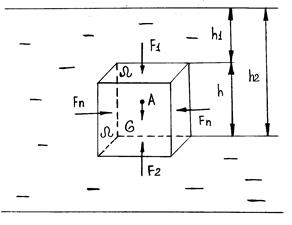
Рис. 2.26

Рассмотрим силы, действующие на погруженное в жидкость тело А (рис. 2.26):

1)боковые силы 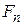. Так как они равны и противоположны, то их равнодействующая равна нулю;

2)сила тяжести тела А, направленная вниз;

3)сила давления жидкости на тело А сверху – ,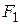

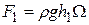; (2.116)

4)сила давления жидкости на тело А снизу – ,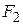

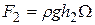; (2.117)

Суммарная сила давления жидкости на погруженное тело, или выталкивающая сила, будет равна

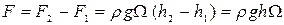. (2.118)

Но т.к. 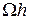– есть объём погруженного тела А, то выталкивающая сила

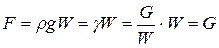. (2.119)

Следовательно, подъёмная, или выталкивающая, сила, действующая на погруженное в жидкость тело, равна весу жидкости, вытесненной данным телом.

Величина выталкивающей силы не зависит от глубины погружения тела и на различной глубине будет постоянной.

Гидродинамика

Задачи гидродинамики

Гидродинамика изучает закономерности движения жидкости и применение их в инженерной графике. Основные трудности изучения движения реального тела обусловлены самой природой жидкости и сложностью учёта вязкости сил внутреннего трения и трения жидкости о стенки канала. По предложению Л. Эйлера изучение гидродинамики начинают с рассмотрения идеальной (совершенной), невязкой жидкости, внося затем в найденные уравнения коррективы для учёта сил трения реальных жидкостей.

Основной задачей гидродинамики является определение величин, характеризующих движение жидкости: скорости течения и гидродинамического давления. Если эти факторы зависят только от координат рассматриваемой частицы, движение называется установившимся; если от координат и от времени, то движение – неустановившееся.

Задачей гидродинамики является так же нахождение зависимости между основными факторами движения, координатами и временем.

Основные понятия. Модель движения.

Направленную движущуюся массу жидкости называют потоком. Кроме скоростей и давления, координат и времени, относящихся к отдельным частицам, поток в целом характеризуется ещё и формой поперечного сечения. Форма потока обычно определяется сечением канала, в котором движется жидкость. Жидкость может заполнять всё сечение канала, или только часть сечения. В последнем случае у потока имеется свободная поверхность и можно говорить о глубине потока.

Движение потока, как и отдельной частицы, может быть установившимся и неустановившимся. Примером установившегося движения является движение воды в реках, и каналах при постоянных уровнях свободной поверхности, так же движение жидкости в трубах или её истечение через отверстие при постоянном напоре (например, холостой ход работы двигателя, бензонасос, помпа, масляный насос). Если же в реках и каналах уровни воды с течением времени изменяются (паводок) или движение в трубах и через отверстия происходит при переменном напоре, то движение жидкости в этих случаях будет.

В свою очередь установившееся движение жидкости может быть равномерным и неравномерным.

Равномерным движением жидкости называется такое движение, при котором её частицы, перемещаясь вдоль оси потока от одного поперечного сечения к другому, сохраняют свою скорость постоянной по величине и по направлению. Равномерное движение жидкости возможно только при постоянном поперечном сечении потока по всей его длине (применение – движение жидкости в цилиндрических трубах). Неравномерное движение жидкости наблюдается в открытых руслах и трубах с изменяющимися поперечными сечениями, что приводит к изменению скоростей по длине потока.

По степени заполнения потоком поперечного сечения канала различают напорное и безнапорное движение жидкости.

При напорном движении поток жидкости ограничен твёрдыми стенками по всему периметру поперечного сечения, например, в водопроводных трубах.

При безнапорном движении поток жидкости ограничен твёрдыми стенками только по части периметра поперечного сечения. Движение в этом случае происходит только под влиянием сил тяжести, вследствие текучести жидкости. Напорное же движение осуществляется под влиянием сил тяжести и разности давлений в начале и в конце трубопровода.

Во многих случаях для удобства и упрощения теоретических расчётов движения жидкости реальный поток мысленно считается состоящим из бесконечного числа элементарных струек. Это позволяет результаты исследований, приведённых для элементарной струйки, распространить с соответствующими поправками на весь поток жидкости.

Принимая для исследований струйчатую модель реального потока, считают, что все частицы жидкости перемещаются в потоке по так называемым линиям тока (рис. 3.1)

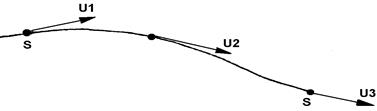
Рис.3.1

Линией тока называется кривая S-S, проведённая в жидкости по направлению её движется таким образом, что векторы скоростей 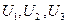в каждой её точке направлены к этой кривой.

Построим вокруг точки А (рис 3.1) замкнутый элементарный контур, образующий элементарную площадку 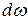. Если через все точки этого контура провести линии тока, то получим так называемую трубку тока, которая и образует элементарную струйку движущейся жидкости.

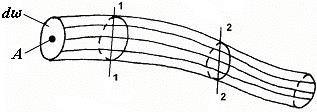
Рис.3.2

Так как в реальном потоке жидкость перемещается как единое физическое тело и в действительности трубок тока не существует, то и свойства, которыми наделяется элементарная струйка, являются условными.

В установившемся движении элементарная струйка имеет следующие свойства:

1. Форма элементарной струйки постоянна и не изменяется с течением времени, поскольку рассматривается установившееся движение.

2. Частицы жидкости не могут переходить из одной струйки в другую, т.к. струйки ограничены линиями тока, которые векторы скорости не пересекают, а являются касательными к ним.

3. Скорости во всех точках какого-либо поперечного сечения, ввиду его малости, одинаковы.

Основными гидравлическими элементами движения потока жидкости являются скорость, живое сечение и расход.

Скорость движения жидкости в какой-либо точке поперечного сечения потока в дальнейшем будем обозначать через u. Для реальных потоков эта скорость является величиной переменной, зависящей от местоположения точки в рассматриваемом поперечном сечении потока.

Живым сечением потока называется поверхность поперечного сечения, нормальная к местному значению вектора скорости 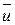в каждой своей точке.

Для потока жидкости живое сечение 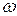сложится из суммы живых сечений элементарных струек.

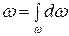. (3.1)

Кроме площади 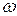характеристиками живого сечения являются смоченный периметр f, представляющий длину контура живого сечения, по которому жидкость соприкасается с неподвижными твёрдыми стенками и гидравлический радиус R, который есть отношение площади живого сечения 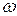к смоченному периметру f.

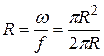. (3.2)

Гидравлический радиус характеризует форму живого сечения и может быть разным при одинаковых значениях 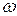. Для круглого живого сечения гидравлический радиус численно равен половине геометрического радиуса.

Расходом называется количество жидкости, проходящей через данное живое сечение в единицу времени.

Полный расход потока жидкости составится из суммы расходов элементарных струек, взятых в пределах данного живого сечения потока

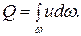(3.3)

Для большинства реальных потоков не всегда удаётся математически установить закон распределения местных скоростей в поперечном сечении потока и проинтегрировать уравнение (3.3). Поэтому для решения данной задачи прибегают к понятию о средней скорости потока.

Средней скоростью потока V называется такая условная скорость, произведение которой на площадь поперечного сечения потока равно его расходу

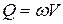. (3.4)

Следовательно, средняя скорость реального потока в каком-либо его сечении может быть определена из соотношения.

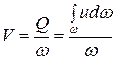. (3.5)

Уравнения неразрывности