Интегральная формулировка закона сохранения заряда

Исходя из закона сохранения заряда, как экспериментального факта можно записать:

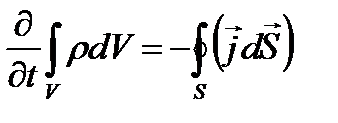. (3.1)

Это означает: что изменение со временем заряда внутри объема 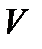может происходить либо за счет втекания, либо за счет вытекания зарядов через замкнутую поверхность 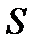, ограничивающую этот объем. Напомним что у замкнутых поверхностей положительной нормалью является вектор 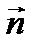т.е. изменение заряда может быть связано с потоком плотности тока

Знак (-) учитывает тот факт, что если положительный заряд внутри объема уменьшается, то плотность тока направлена под острым углом к вектору положительной нормали к поверхности.

Воспользуемся формулой Остроградского-Гаусса:

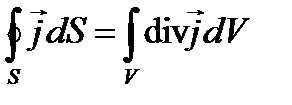, (3.2)

тогда

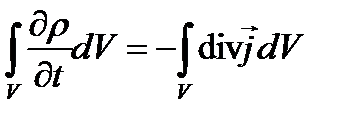
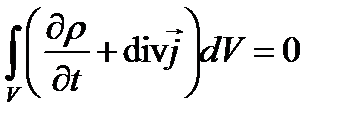
и в силу произвольности объема 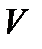можно заключить, что подынтегральное выражение равно нулю, т.е. справедливо соотношение

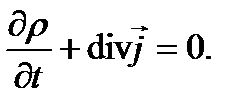(3.3)

Выражение (3.3) является записью закона сохранения заряда в дифференциальной форме и часто (3.3) называют уравнением непрерывности